ML模型4-2：SVM之软间隔支持向量机

软间隔支持向量机

1. 问题引入

在实际任务中，很难确定一个线性可分的超平面（存在某些异常点，这些点不能满足函数间隔≥1的约束条件）；或者说找到了合适的超平面，也很难断定这个貌似线性可分的结果是否由于过拟合导致。

为了包容异常点或者为了避免过拟合，我们允许SVM在一些样本上出错（e.g 下图红色圈中的样本没有划分正确），此时最大化的间隔称为"软间隔"。

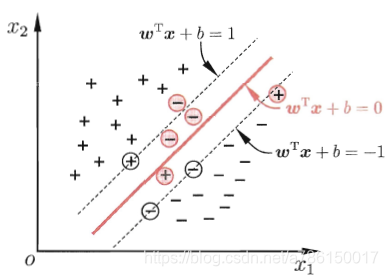
而在线性可分SVM中要求所有样本都满足约束条件（所有样本划分正确），此时最大化的间隔也称为"硬间隔"。

2. 模型描述 - 软间隔最大化

回顾线性可分SVM，它的优化问题是
$$\underset{w,b}{\min }\frac{1}{2}{\Vert w\Vert }^2$$

$$s.t.y_i\left(w^T{x}_i+b\right)\ge 1,i=1,2...m$$
软间隔考虑异常点的情况，约束条件变成：
$$y_i\left(w^T{x}_i+b\right)\ge 1-{\xi }_i,i=1,2...m$$

其中 ${\xi }_i\ge 0$ 称为松弛变量，也就是说我们对样本到超平面的函数距离约束放松了。但如果 ${\xi }_i$ 任意大，会导致任意的超平面都符合要求。所以，目标函数上应该考虑 ${\xi }_i$ 的成本：
$$\underset{w,b}{\min }\frac{1}{2}{\Vert w\Vert }^2+C\sum _{i=1}^m{\xi }_i$$

其中 $C>0$ 是正则化惩罚系数，用来权衡目标函数中的两项（“寻找间隔最大的超平面"和"保证数据点偏差最小”）。$C$ 越大，对误分类的惩罚越大；$C$ 越小，对误分类的惩罚越小。

原始最优化问题
$$\underset{w,b}{\min }\frac{1}{2}{\Vert w\Vert }^2+C\sum _{i=1}^m{\xi }_i$$$$s.t.y_i\left(w^T{x}_i+b\right)\ge 1-{\xi }_i,i=1,2...m$$$${\xi }_i\ge 0,i=1,2...m$$等价于最优化问题（合页损失函数）
$$\underset{w,b}{\underbrace{min}}\sum _{i=1}^m{[1-y_i(w\bullet x_i+b)]}_{+}+\lambda {\Vert w\Vert }^2$$
注：$$\lambda =\frac{1}{2C},[1-y_i(w\bullet x_i+b){]}_{+}={\xi }_i$$
在sklearn中的参数是 $\lambda$。

3. 模型求解

和线性可分SVM的模型求解方法类似，具体如下所述。
1）优化目标为：
$$\underset{w,b}{\min }\frac{1}{2}{\Vert w\Vert }^2+C\sum _{i=1}^m{\xi }_i$$

$$s.t.y_i\left(w^T{x}_i+b\right)\ge 1-{\xi }_i,i=1,2...m$$

$${\xi }_i\ge 0,i=1,2...m$$

2）将约束条件加入目标函数中，得到拉格朗日函数：
$$L\left(w,b,\xi ,\alpha ,\mu \right)=\frac{1}{2}{\Vert w\Vert }^2+C\sum _{i=1}^m{\xi }_i-\sum _{i=1}^m{\alpha }_i\left(y_i\left(w^T{x}_i+b\right)-1+{\xi }_i\right)-\sum _{i=1}^m{\mu }_i{\xi }_i$$

其中 ${\alpha }_i\ge 0,\xi \ge 0$ 均为拉格朗日系数。

3）原始问题转换成对偶问题求解：
$$\underset{w,b,\xi }{\min }\underset{\alpha ,\mu }{\max }L\left(w,b,\xi ,\alpha ,\mu \right)\iff \underset{\alpha ,\mu }{\max }\underset{w,b,\xi }{\min }L\left(w,b,\xi ,\alpha ,\mu \right)$$

4）对偶问题求解：
先求优化函数对于 $w,b,\xi$ 的极小值，求偏导：
$$\begin{array}{rl}\frac{\partial L}{\partial w}& =w-\sum _{i=1}^m{\alpha }_i{y}_i{x}_i=0\Rightarrow w=\sum _{i=1}^m{\alpha }_i{y}_i{x}_i\\ \frac{\partial L}{\partial b}& =\sum _{i=1}^m{\alpha }_i{y}_i=0\Rightarrow \sum _{i=1}^m{\alpha }_i{y}_i=0\\ \frac{\partial L}{\partial \xi }& =0\Rightarrow C-{\alpha }_i-{\mu }_i=0\end{array}$$

将其代回优化函数$L\left(w,b,\alpha \right)$，消去 $w$ 和 $C$，得到和线性可分SVM一样的目标函数，但约束条件不同：
$$\underset{\alpha }{\max }-\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j{x_i}^T{x}_j+\sum _{i=1}^m{\alpha }_i$$

$$s.t.\sum _{i=1}^m{\alpha }_i{y}_i=0$$

$$C-{\alpha }_i-{\mu }_i=0$$

$${\alpha }_i\ge 0,{\mu }_i\ge 0,i=1,2...m$$

对于后面三个约束条件，可以消去 ${\mu }_i$， 只留下 ${\alpha }_i$。同时目标函数变号，求极小：
$$\underset{\alpha }{\min }\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j{x_i}^T{x}_j-\sum _{i=1}^m{\alpha }_i$$

$$s.t.\sum _{i=1}^m{\alpha }_i{y}_i=0,0\le {\alpha }_i\le C,i=1,2...m$$

同理，也是用SMO算法对 $\alpha$ 求极小。

在SMO算法求得 ${\alpha }^{\ast }$ 后，若某样本点的 ${{\alpha }_i}^{\ast }$ 满足 $0<{{\alpha }_i}^{\ast }<C$， 则可依据 $y_i\left(w^T{x}_i+b\right)=1$ 对 $b$ 进行求解。（具体原因参见第4.2节）

4.支持向量

4.1 硬间隔最大化的支持向量

根据KKT的对偶互补条件，最优化问题的解 ${\alpha }^{\ast }$需满足：$${{\alpha }_i}^{\ast }\left(y_i\left(w^T{x}_i+b\right)-1\right)=0$$

又因为线性可分SVM的支持向量均满足 $y_s\left(w^T{x}_s+b\right)=1$，所以
$$\begin{array}{rl}{{\alpha }_i}^{\ast }>0& \iff y_i\left(w^T{x}_i+b\right)=1\Rightarrow 样本都在支持向量上\\ {{\alpha }_i}^{\ast }=0& \iff y_i\left(w^T{x}_i+b\right)\ge 1\Rightarrow 样本都在支持向量上或已被正确分类\end{array}$$

4.2 软间隔最大化的支持向量

根据KKT的对偶互补条件，最优化问题的解 ${\alpha }^{\ast }$需满足：$${{\alpha }_i}^{\ast }\left(y_i\left(w^T{x}_i+b\right)-1+{\xi }_i\right)=0,{{\mu }_i}^{\ast }{\xi }_i=0$$

约束条件有 ${\alpha }_i+{\mu }_i=C$ ，所以有
$$\begin{array}{rl}a)& {{\alpha }_i}^{\ast }=0\Rightarrow {{\mu }_i}^{\ast }=C\Rightarrow {\xi }_i=0\\ & \Rightarrow y_i\left(w^T{x}_i+b\right)\ge 1-{\xi }_i\\ & \Rightarrow y_i\left(w^T{x}_i+b\right)\ge 1\Rightarrow 在间隔边界上/已被正确分类\\ b)& 0<{{\alpha }_i}^{\ast }<C\Rightarrow y_i\left(w^T{x}_i+b\right)-1+{\xi }_i=0\\ & \Rightarrow {{\mu }_i}^{\ast }̸=0\Rightarrow {\xi }_i=0\\ & \Rightarrow y_i\left(w^T{x}_i+b\right)=1\Rightarrow 在间隔边界上\\ c)& {{\alpha }_i}^{\ast }=C\Rightarrow {{\mu }_i}^{\ast }=0\Rightarrow {\xi }_i̸=0\\ & \Rightarrow y_i\left(w^T{x}_i+b\right)=1-{\xi }_i\\ & i)0\le {\xi }_i\le 1时，点被正确分类，但在超平面和间隔边界之间\\ & ii){\xi }_i=1时，点在超平面上，无法被正确分类\\ & ii){\xi }_i>1时，点在超平面另一侧，被误分\end{array}$$

软间隔的支持向量是对应于 ${{\alpha }_i}^{\ast }>0$ 的样本点的实例，可能在间隔边界上，可能在超平面和间隔边界之间，也可能在被误分的一侧。

Ref

支持向量机原理(二) 线性支持向量机的软间隔最大化模型
SVM系列第七讲–KKT条件