有限长离散变换:离散傅里叶变换
Finite-Length Discrete Transforms: DFT(Discrete Fourier Transform)
1.正交变换(Orthogonal Transforms)
若对于基序列 ψ[k,n],有:
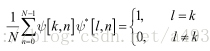
那么对于有限长度的序列x[n](0≤n≤N-1),其正交变换与正交反变换的系数为:
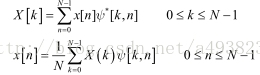
2.DFT的定义式
若使用旋转引子(twiddle factor)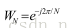 来表示DFT,那么有:
来表示DFT,那么有:
正变换(DFT):

反变换(IDFT):
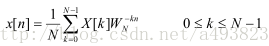
3.DFT的矩阵形式
用矩阵形式来表示DFT,那么若设原信号与频谱分别为:
那么傅里叶基变换矩阵为:
那么对于,DFT的矩阵形式就可以写作:
4.DFT与DTFT的关系
离散傅里叶变换(DFT)X[k]是由在序列x[n]的DTFT的区间0≤ω≤2π以间隔2π/N等间隔取样得到的,即:
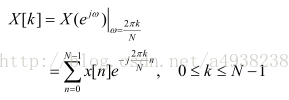





 本文深入解析了有限长离散变换中的离散傅里叶变换(DFT),包括正交变换的概念、DFT的定义式及其矩阵表示形式,并探讨了DFT与离散时间傅里叶变换(DTFT)之间的关系。
本文深入解析了有限长离散变换中的离散傅里叶变换(DFT),包括正交变换的概念、DFT的定义式及其矩阵表示形式,并探讨了DFT与离散时间傅里叶变换(DTFT)之间的关系。
















 2752
2752

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








