滑动窗口最大值P239

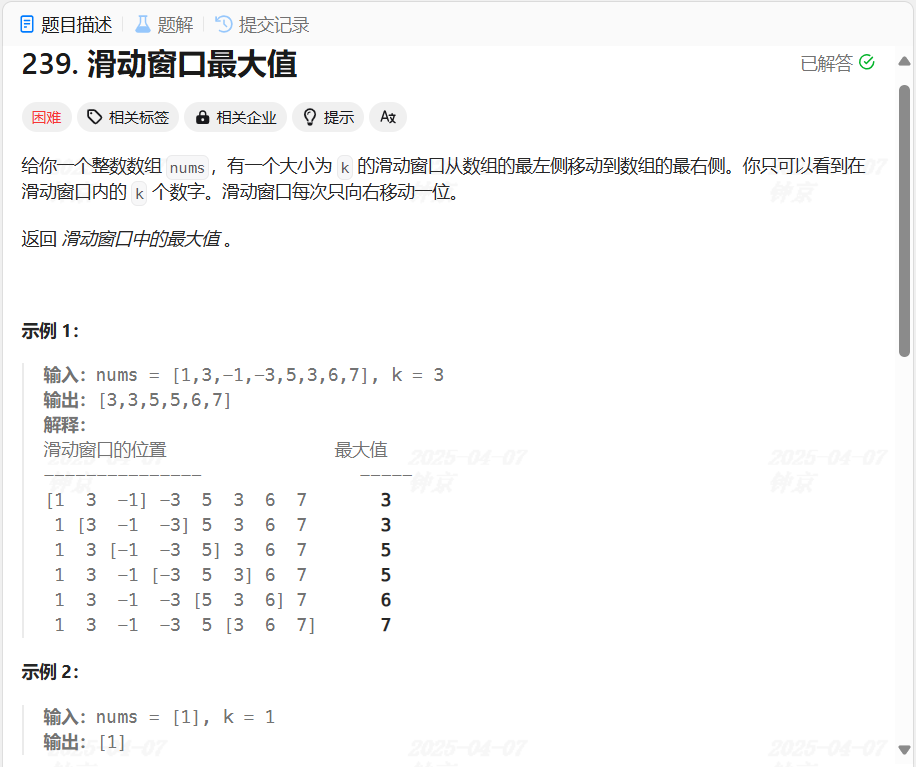
原题

方法一:暴力破解(超时)

public int[] maxSlidingWindow(int[] nums, int k) {
    // 用于模拟滑动窗口的队列
    LinkedList<Integer> list = new LinkedList<>();

    // 存储每个窗口的最大值
    List<Integer> res = new ArrayList<>();

    for (int i = 0; i < nums.length; i++) {
        // 将当前元素加入窗口
        list.add(nums[i]);

        // 窗口未满时跳过
        if (list.size() < k) continue;

        // 计算当前窗口中的最大值并加入结果
        res.add(Collections.max(list));

        // 移除窗口最左侧的元素，滑动窗口向右滑动
        list.removeFirst();
    }

    // 最后将结果列表转为 int 数组返回
    return res.stream().mapToInt(Integer::intValue).toArray();
}

时间复杂度分析
外层循环执行 n 次，其中 n 是数组 nums 的长度。

每次窗口大小达到 k 时，调用 Collections.max(list)：

list 的大小为 k，找最大值为 O(k)。

所以，总时间复杂度是：O((n - k + 1) * k) ≈ O(nk)
👉 当 k 较小时还可以接受，但 k 较大时会严重超时（比如 k = 5000，n = 10000）。

空间复杂度分析
list 的大小最多为 k，空间为 O(k)。
res 的大小为 n - k + 1，空间为 O(n)。
所以总体空间复杂度为：O(n)

方法2:双端队列+滑动窗口
核心思想:
使用 双端队列（Deque） 来维护一个“单调递减”的队列，队首始终是当前窗口的最大值索引。
每次滑动窗口向右移动时，只做两件事：
弹出已经滑出窗口的索引（过期元素）
弹出所有比当前元素小的队尾索引（它们不可能成为最大值）

public int[] maxSlidingWindow(int[] nums, int k) {
    if (nums == null || nums.length == 0 || k == 0) {
        return new int[0]; // 边界处理
    }

    List<Integer> res = new ArrayList<>();
    Deque<Integer> deque = new LinkedList<>(); // 存储索引，不是元素本身

    for (int i = 0; i < nums.length; i++) {
        // 如果队头元素已经不在当前窗口范围内，移除它
        if (!deque.isEmpty() && deque.peekFirst() < i - k + 1) {
            deque.pollFirst();
        }

        // 移除所有比当前元素小的队尾元素（保持单调递减）
        while (!deque.isEmpty() && nums[deque.peekLast()] < nums[i]) {
            deque.pollLast();
        }

        // 把当前索引加入队尾
        deque.offerLast(i);

        // 只有当窗口形成之后，才记录结果（即 i >= k - 1）
        if (i >= k - 1) {
            res.add(nums[deque.peekFirst()]); // 队首就是当前窗口最大值
        }
    }

    // 把结果 List 转换成 int[]
    return res.stream().mapToInt(Integer::intValue).toArray();
}

时间复杂度是 O(n)
总空间复杂度：O(n)