设计大规模分布式存储系统：从普通哈希到一致性哈希

一、数据库水平扩展的需求与挑战

随着互联网的不断发展，单一数据库面对高并发和大规模数据时，已难以满足业务需求。这时，“水平扩展”（Sharding）成为首选方案。
水平扩展是指将数据按一定规则分散到多个数据库实例（分片）上，各实例并行工作，实现系统横向扩展。

常见挑战：

• 数据定位：如何高效地将数据Key映射到正确的数据库实例？
• 迁移成本：当节点新增或删除时，如何尽可能减少数据迁移量？

传统方案

常用做法是通过哈希函数（如MD5、SHA-256），将Key映射到一定的整数空间，然后求余映射到N台数据库。例如：

serverIndex = hash(key) mod N

如下图5-1所示，例如hash(key0) mod 4 = 1，表示键key0保存在Server1：

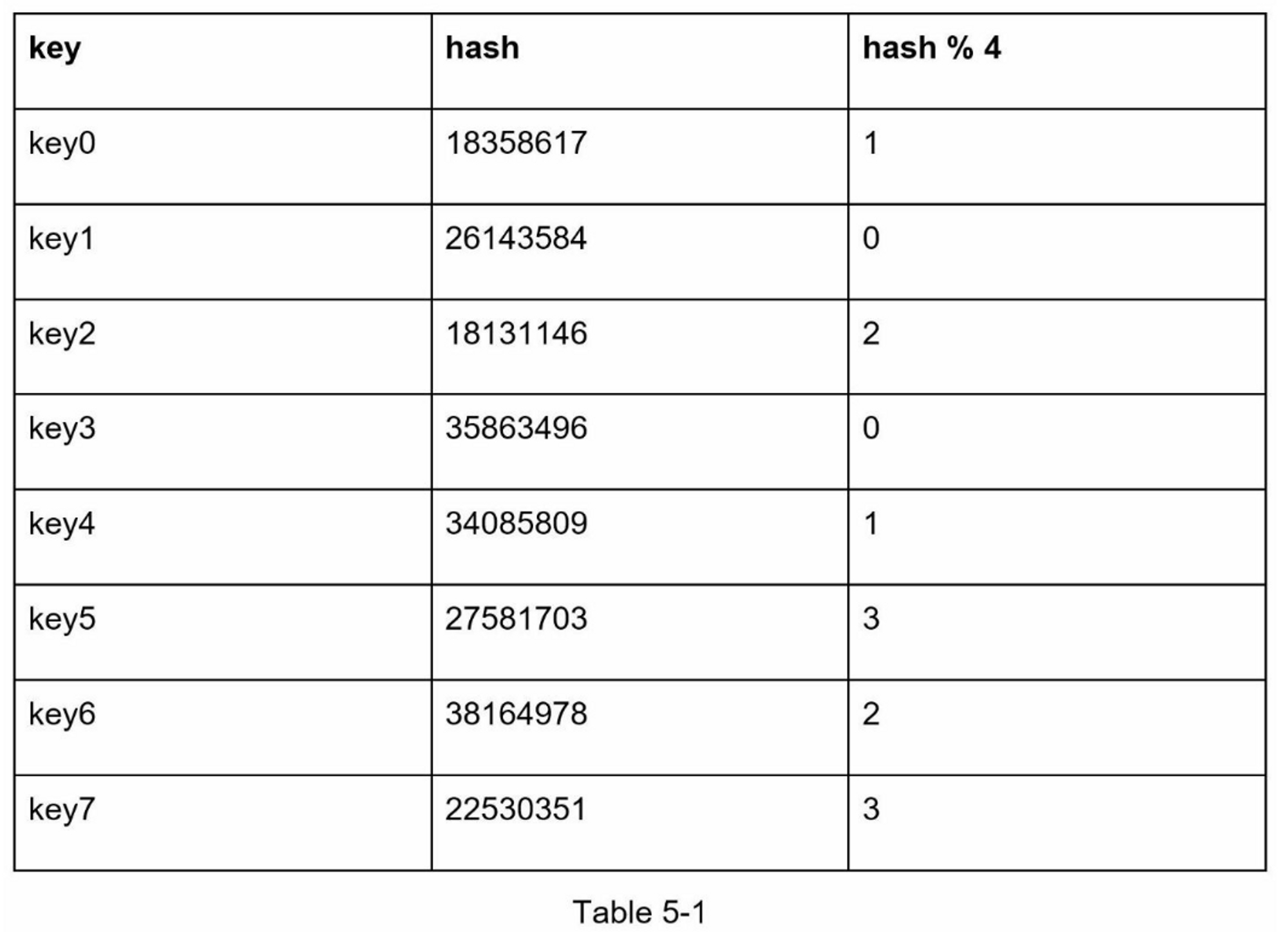
该方法在服务器数量固定、数据分布均匀情况下效果良好。但一旦增减节点，哈希求余操作会造成大量键重新分配。

如下图5-2，如果删除Server1，N变为3，绝大部分数据分布都会变化，带来缓存失效：

---

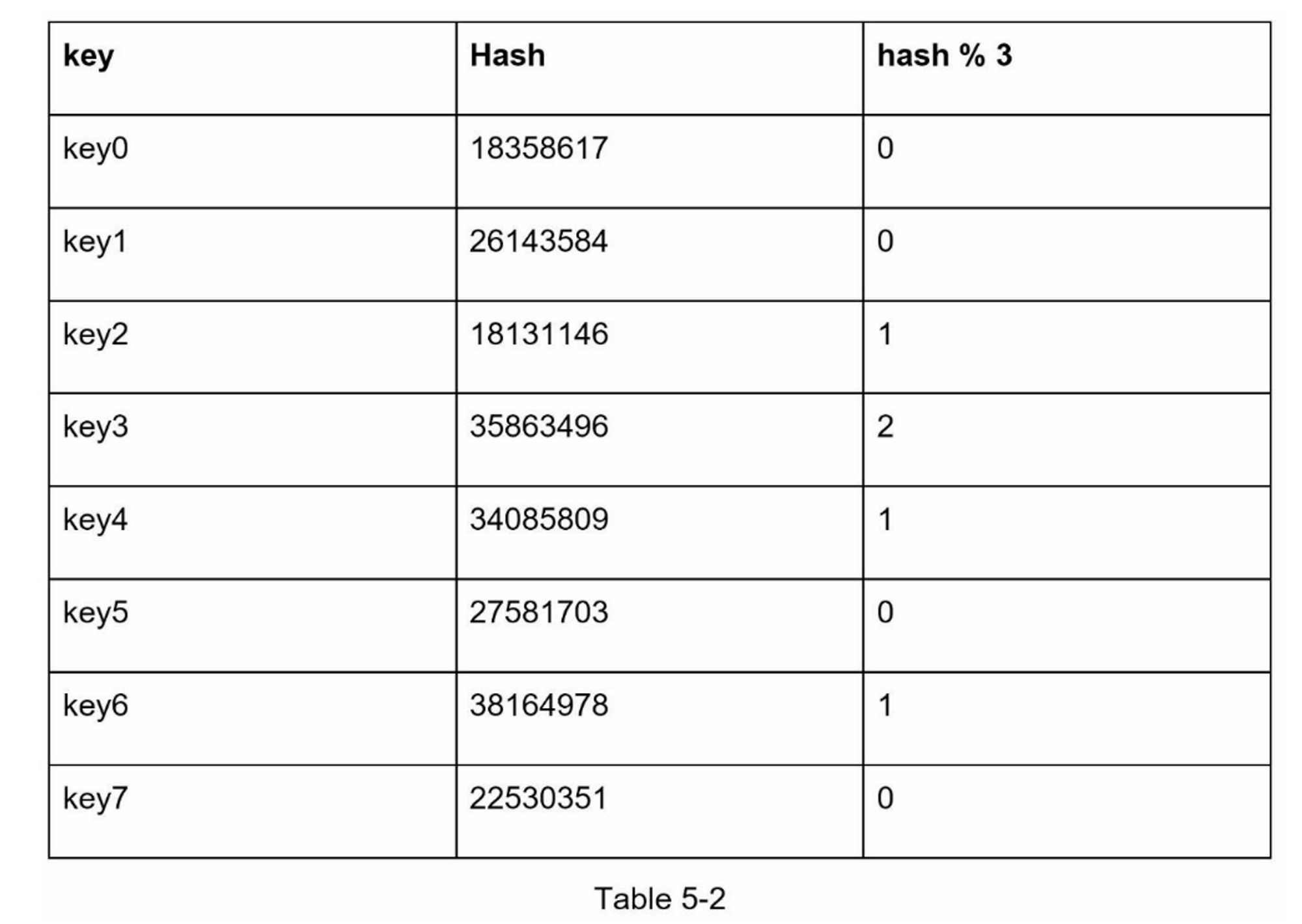
二、一致性哈希

一致性哈希是一种特殊哈希算法，可以显著减少因节点改变带来的数据迁移。假设有 $k$ 个键、$n$ 个槽点（节点），平均仅需重新映射 $k/n$ 的数据，而传统哈希几乎全部重新分配。

---

一致性哈希的特点与优点

特点：

• 节点变动影响小：新增或删除节点时，只有部分数据会迁移，极大减轻迁移负担。
• 分布均匀：通过虚拟节点机制，可以实现大致均匀的负载分配，避免热点。
• 扩展性强：方便横向扩展，只需将新节点的哈希值插入哈希环中，其他节点无需变动。

优点：

• 高效的容错和弹性：支持动态加入与删除节点，系统可灵活扩展或收缩。
• 减少迁移成本：相比传统哈希，迁移数据只涉及部分Key，优化了系统表现。
• 负载平衡性好：结合虚拟节点后，确保各节点负载接近平均，避免某些节点过载。

适用场景：

• 分布式缓存（如Redis Cluster）
• 分布式存储（如Hadoop HDFS块存储）
• 高可用数据库分片
• 内容分发网络（CDN）

---

什么是哈希环（Hash Ring）？

哈希环将整数哈希空间首尾相连形成圆环，大幅缓解节点变动带来的迁移压力：

具体流程：

1. 选定哈希空间（如SHA-1，0~2^160-1），构成圆环。
2. 将服务器节点哈希后映射到环上的某点。
3. 数据Key同样哈希后映射到环上。
4. 每条数据存储在其顺时针遇到的第一个节点上。

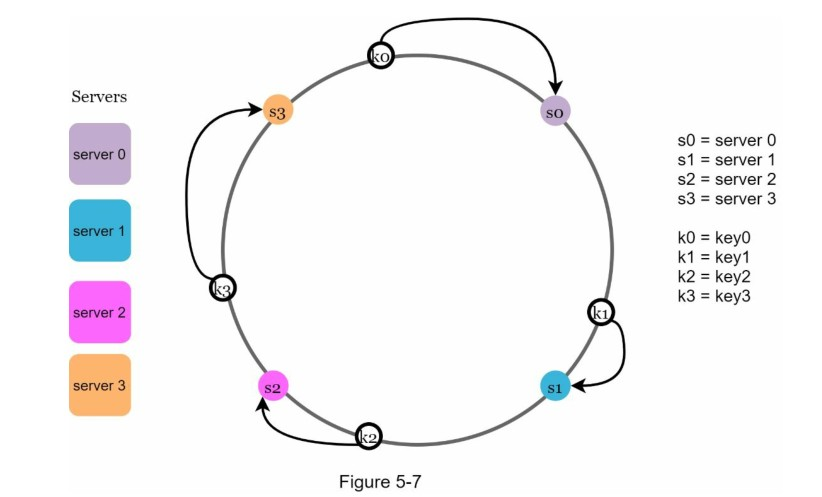
如下图，4台服务器分布于哈希环：

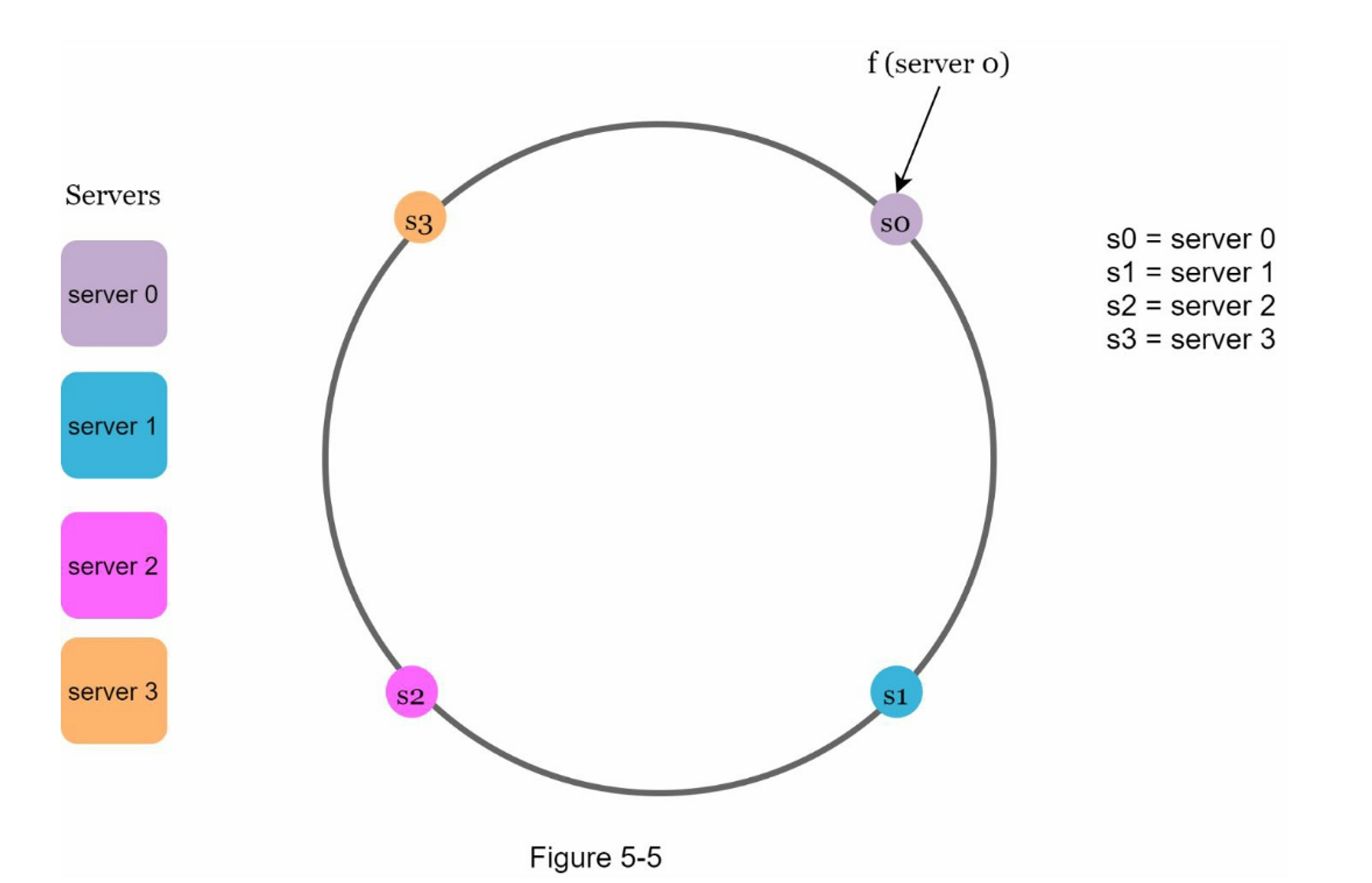
数据Key的分配示意：

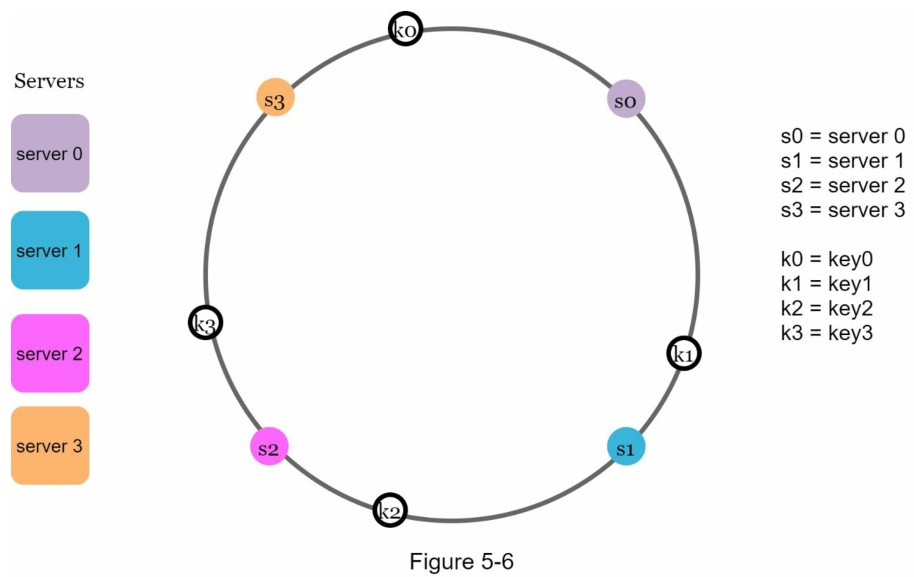
查找思路：顺时针查找，Key落到第一个遇到的节点上。
k0存储在s0、k1存储在s1、k2存储在s2、k3存储在s3

节点变更对数据分布的影响

• 新增节点：只影响部分Key。如下图，Server4新增，仅key0迁移到新节点：

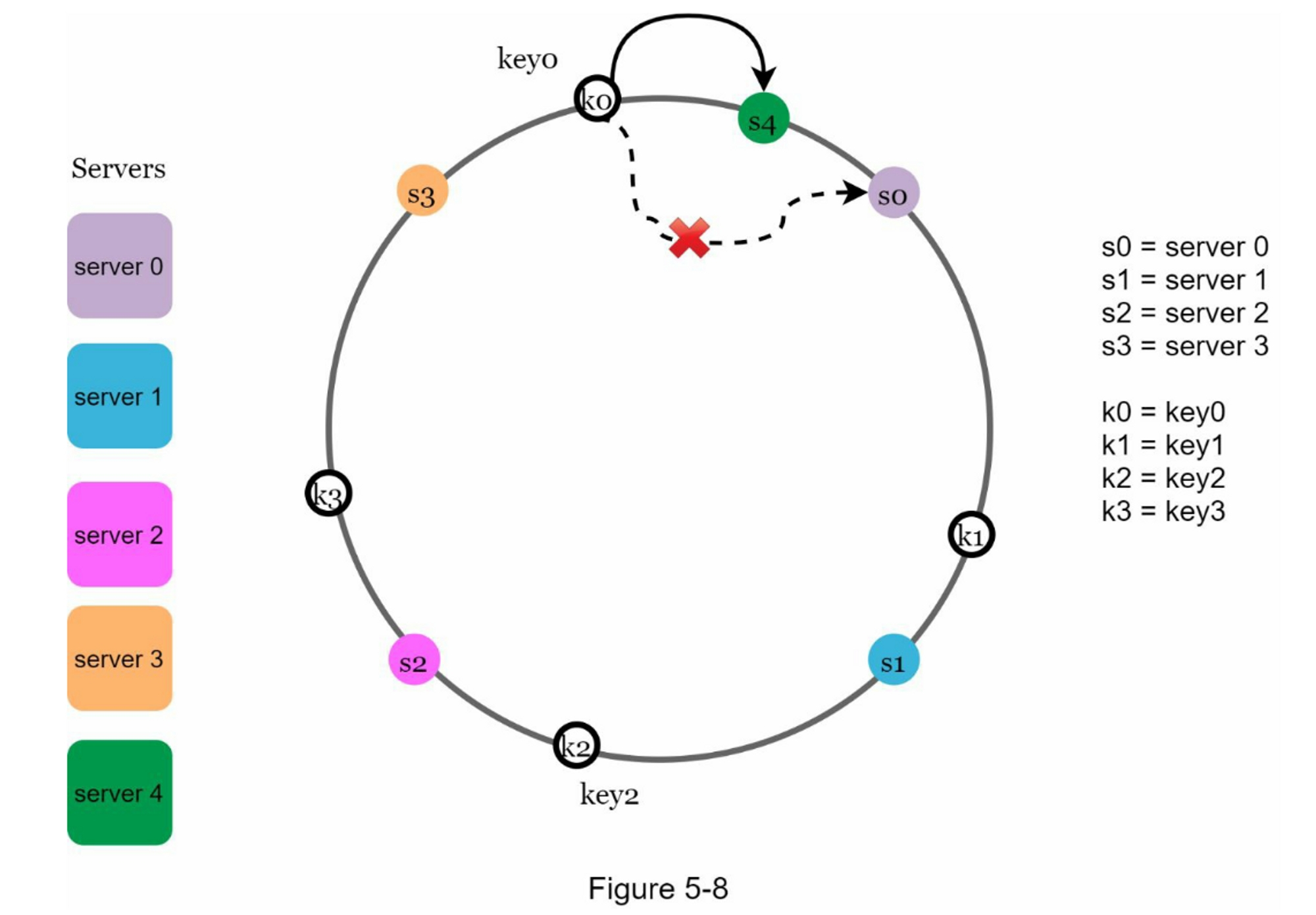
• 移除节点：受影响区域极小，如Server1删除，仅需将key1迁移到Server2：

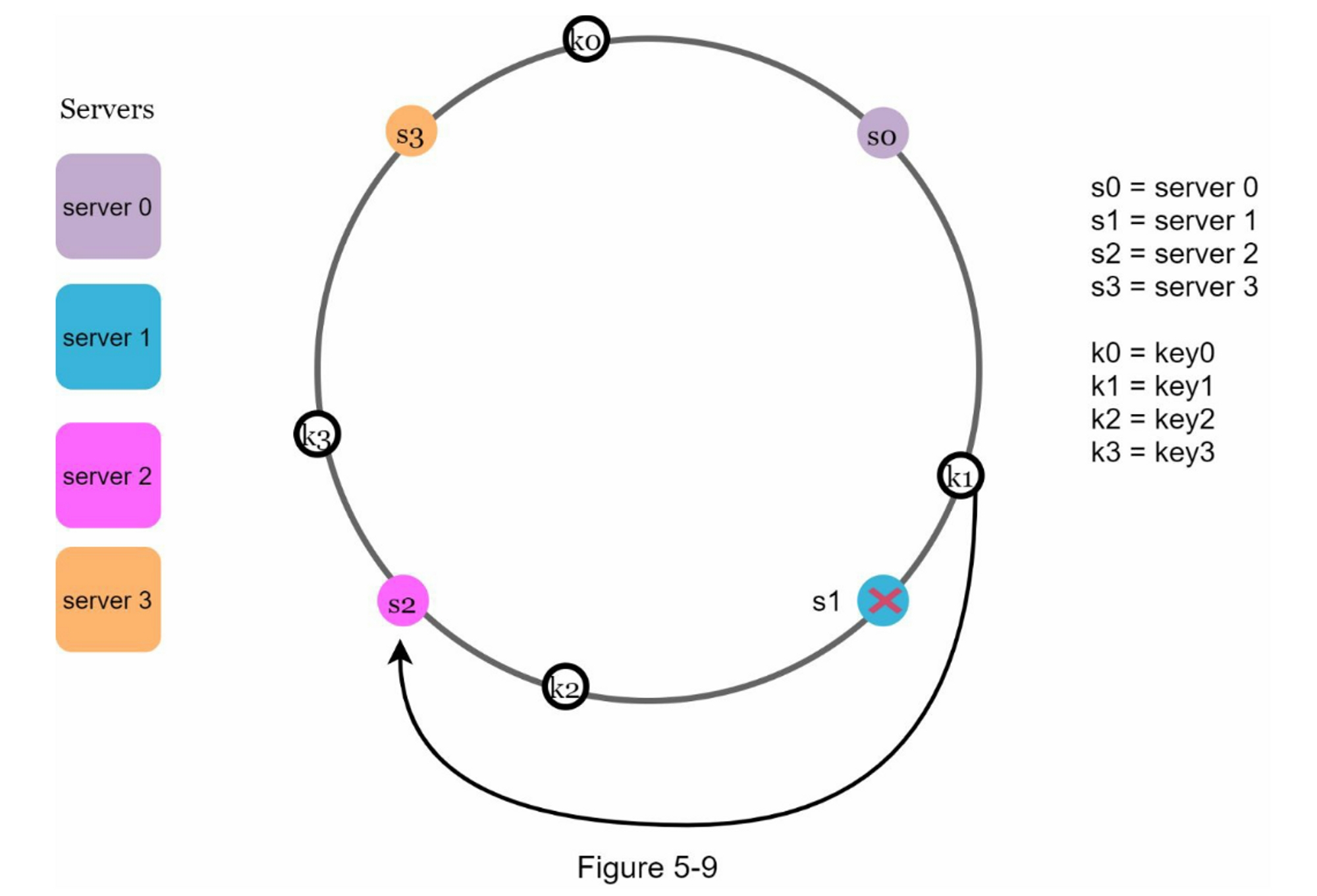
• 影响区域确定：新增Server4时，受影响的是s3与s4之间的区间：

---

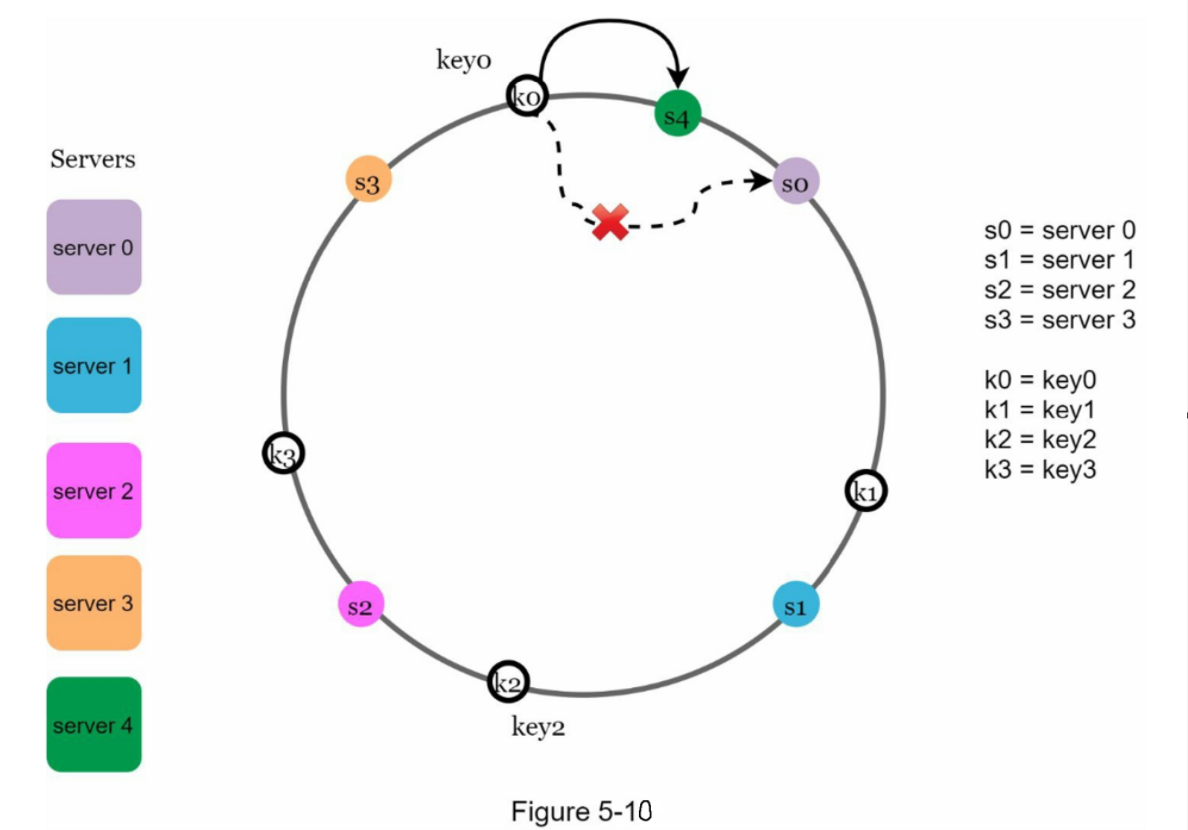
三、一致性哈希的不足及虚拟节点机制

负载不均衡问题

一致性哈希虽然减少了迁移量，但节点分布完全依赖哈希函数，可能：

• 某些节点聚集在一起，负载过重
• 有些节点间距较大，承担大量Key
• 极端情况下，部分节点变为“热点”，形成性能瓶颈

虚拟节点（Virtual Node）方案

为缓解此问题，"虚拟节点"机制应运而生：

• 一个物理节点对应多个虚拟节点，均匀分布到环上
• 数据按一致性哈希分配到虚拟节点，虚拟节点再映射回物理节点
• 显著提升负载均衡性，极大降低热点风险

示例：

假设3台服务器，每台分配3个虚拟节点：

• S1 → S1#1, S1#2, S1#3
• S2 → S2#1, S2#2, S2#3
• S3 → S3#1, S3#2, S3#3

虚拟节点被均匀散布，负载分配趋于平均。

优势对比

	一致性哈希	一致性哈希+虚拟节点
节点变更后数据迁移	局部	局部
负载均匀性	易失衡	更均匀
热点服务器	可能出现	极大缓解
实现复杂度	低	稍高（需额外映射）

虚拟节点数量选取与系统开销

虚拟节点数越多，数据分布越均匀。但虚拟节点越多，运维和映射表开销也更大。例如，虚拟节点达到100个时，负载分布的标准差约为10%；200个则降至5%，但会增大内存与运算消耗。实际应用需要在负载均衡和系统开销间合理权衡。

---

四、方差（Variance）与波动分析

定义：方差衡量数据点离均值的平方平均值，用于描述数据的离散程度。

• 方差越大，数据波动越大，分布越分散
• 方差越小，数据更集中，分布更紧密

公式（数据 $x_1,x_2,...,x_n$，均值$\mu$）：

$${\sigma }^2=\frac{1}{n}\sum _{i=1}^n(x_i-\mu {)}^2$$

---

五、标准差（Standard Deviation）

标准差是方差的平方根，单位与数据一致，用于直观地反映数据的波动幅度。

公式：

$$\sigma =\sqrt{{\sigma }^2}$$

---

实例分析

给定一组数据：4, 6, 8, 10, 12

1. 均值：
   $$\mu =\frac{4+6+8+10+12}{5}=8$$
2. 方差：
   $${\sigma }^2=\frac{(4-8{)}^2+(6-8{)}^2+(8-8{)}^2+(10-8{)}^2+(12-8{)}^2}{5}=8$$
3. 标准差：
   $$\sigma =\sqrt{8}\approx 2.828$$

如果一组数据均值为100，标准差为20，则数据大多落在[80,120]间波动；
标准差为5，则集中于[95,105]。

---

总结

指标	含义	单位	计算方式	直观解释
方差	各数据距均值的平方平均	数据单位平方	平方后求平均	衡量波动大小，但单位不直观
标准差	方差的平方根	与原数据相同	方差开方	实际波动幅度，直观反映平均偏离均值的距离

---