坐标变换与相机参数

目录

1、概念介绍

1.1 针孔模型​​​​​​​

2、四种坐标的介绍

3、坐标转换关系图 

4、世界坐标->相机坐标

 4.1 外参

5、相机坐标->图像坐标 

6、图像坐标->像素坐标

 7、内参

8、投影矩阵M

---

1、概念介绍

1.1 针孔模型

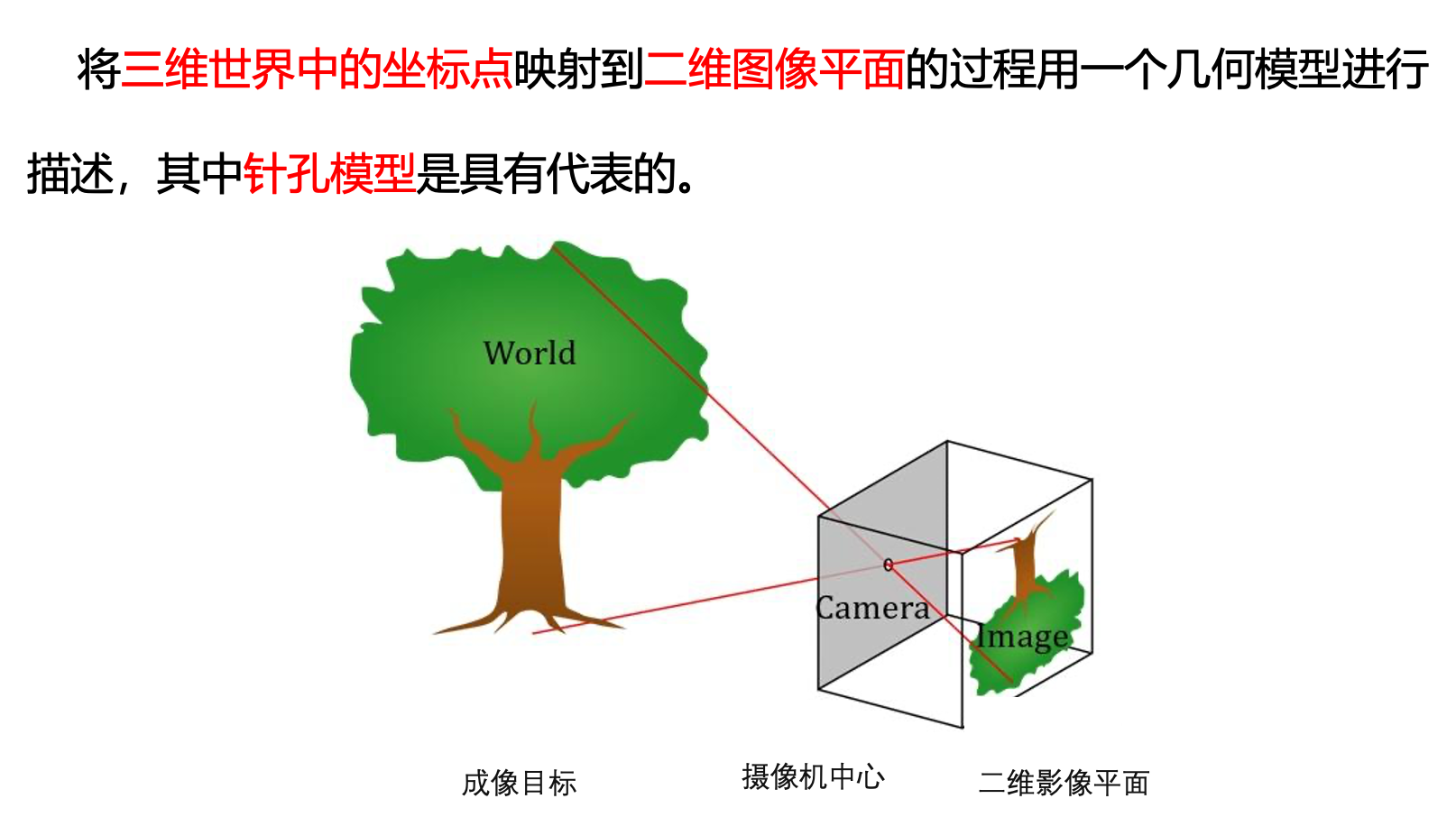
        现实世界中源于某个物体的光线穿过针孔，会在底板上投影成一幅倒立的图像。真实世界的物体即为三维空间的成像目标，针孔为摄像机中心，倒影成像平面则为二维影像平面。

2、四种坐标的介绍

  

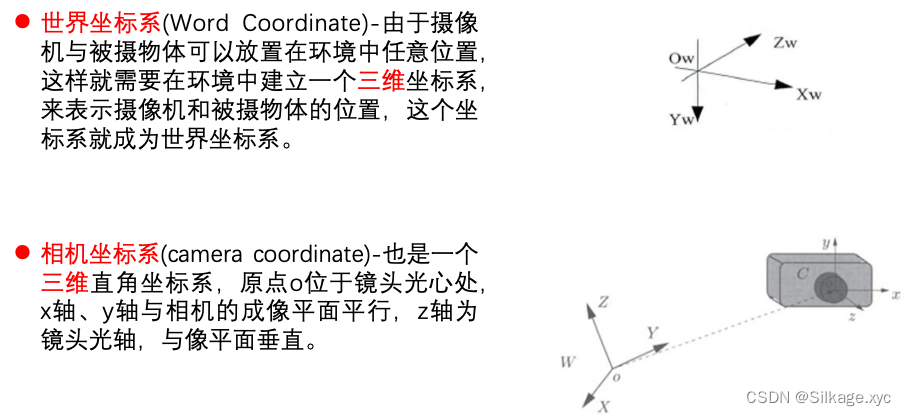
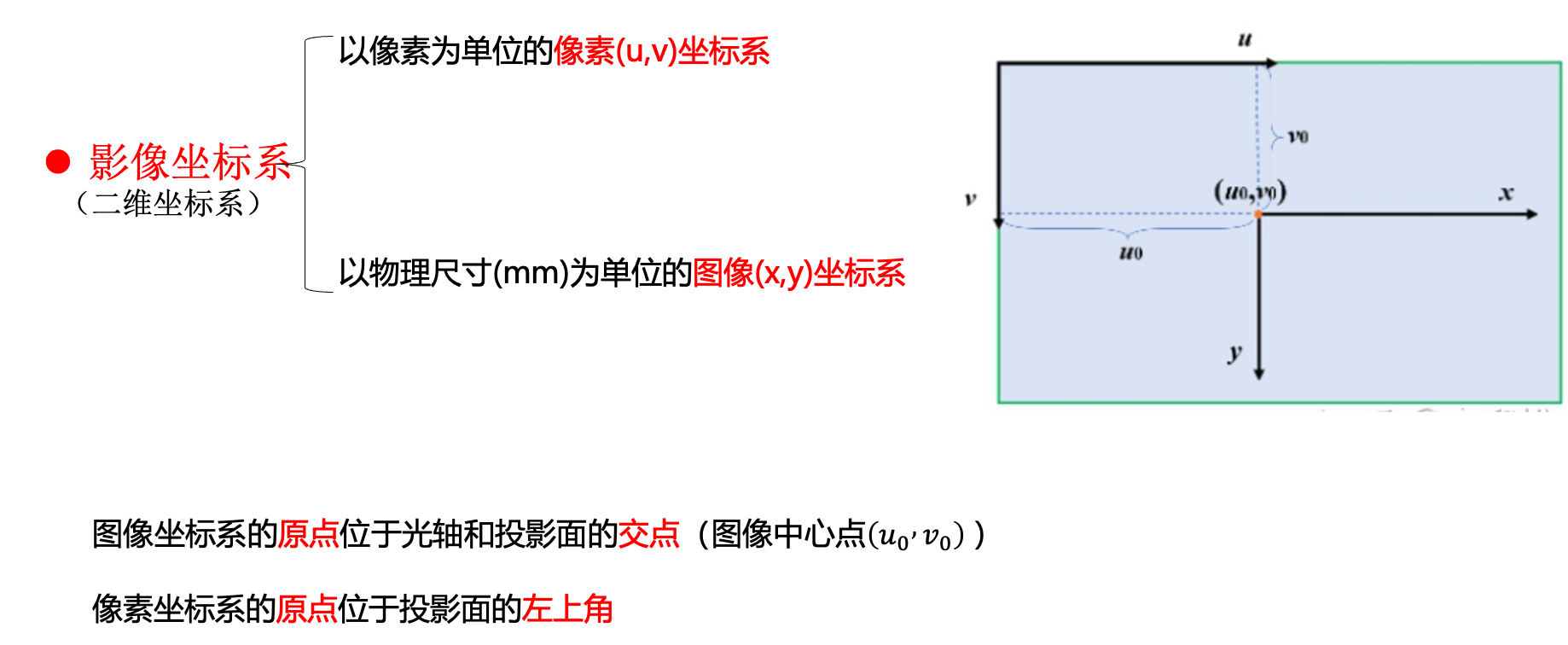
3、坐标转换关系图 

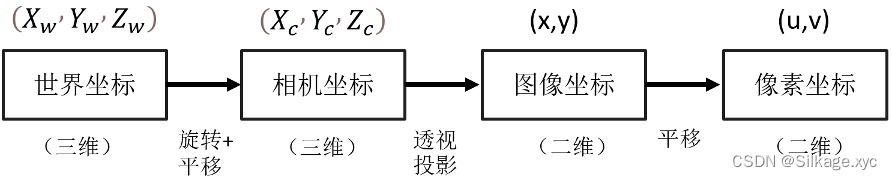
4、世界坐标->相机坐标

三维坐标到三维坐标的转换，只需要简单的旋转+平移即可

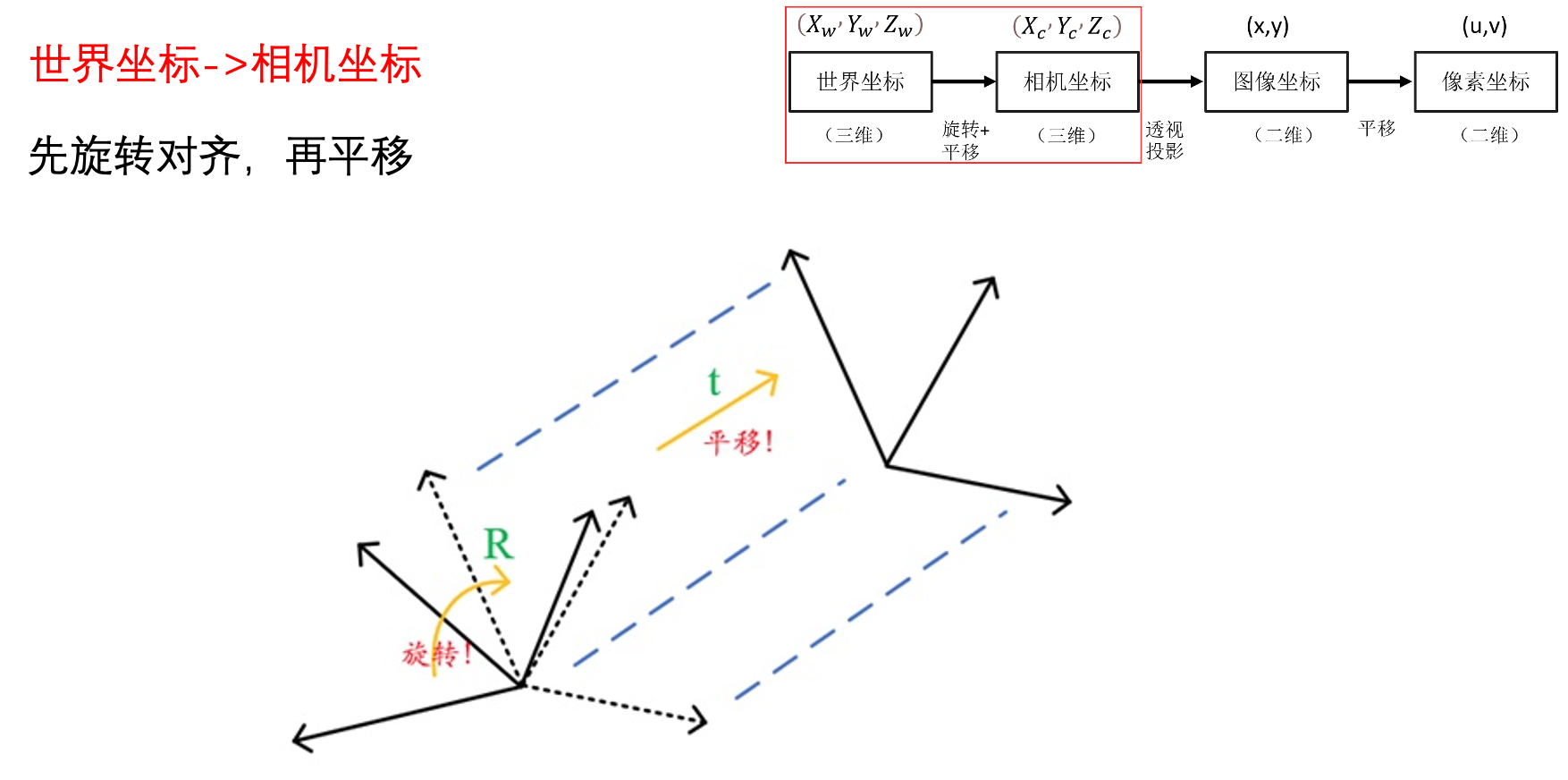
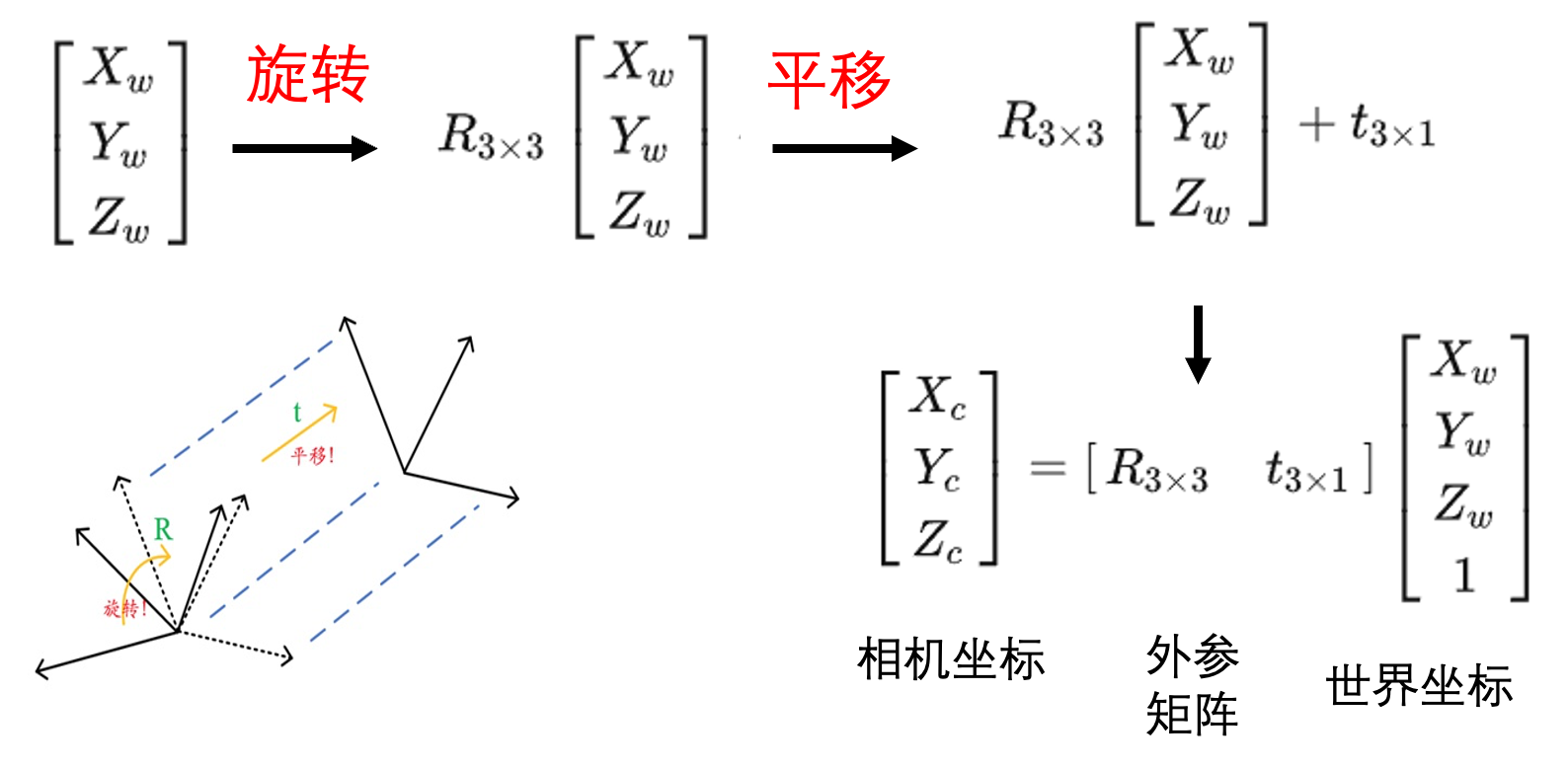
 4.1 外参

        世界坐标转换成相机坐标要乘以外参矩阵得到，外参描述的是世界坐标到相机坐标之间的转换关系。

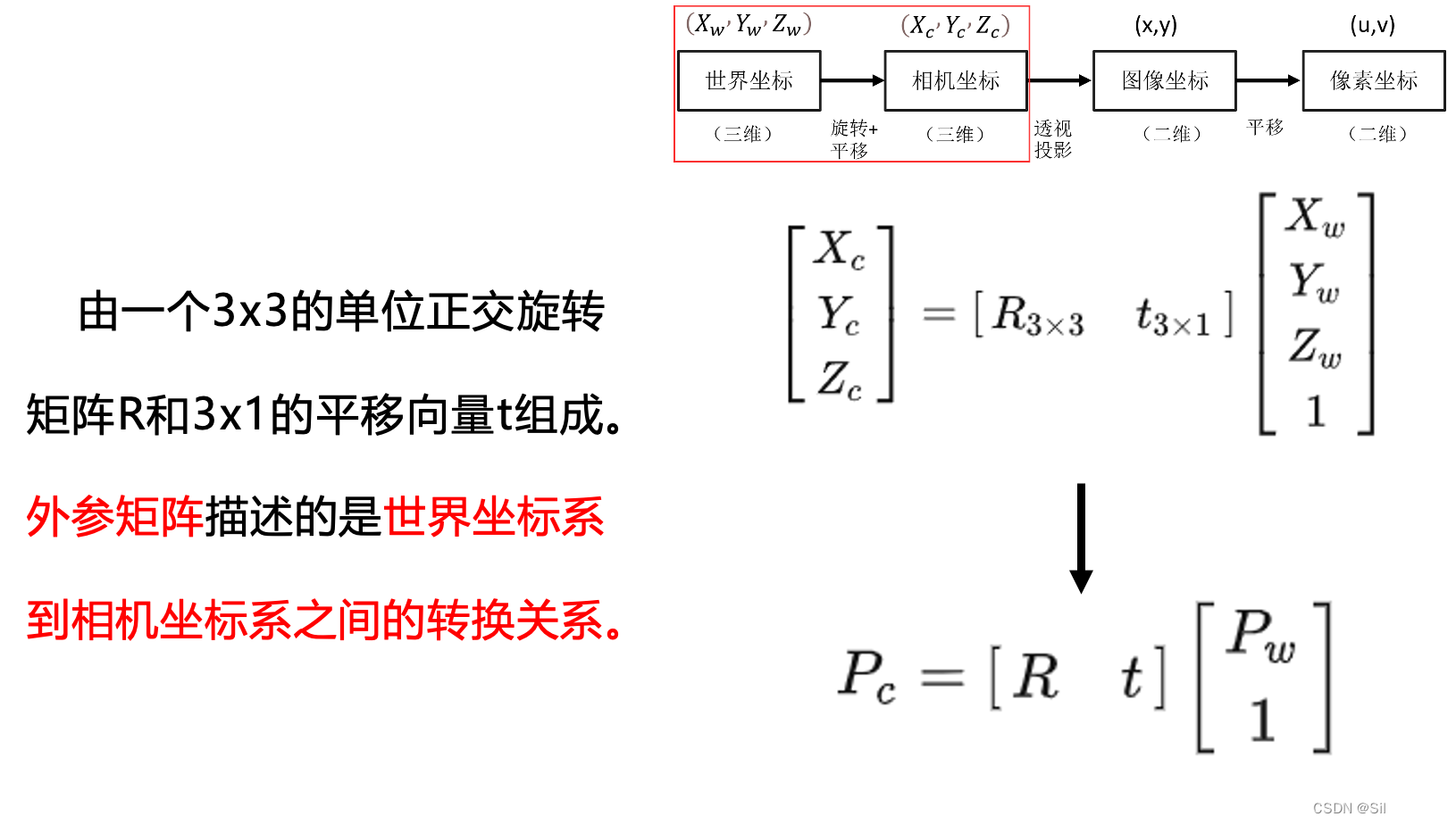
5、相机坐标->图像坐标 

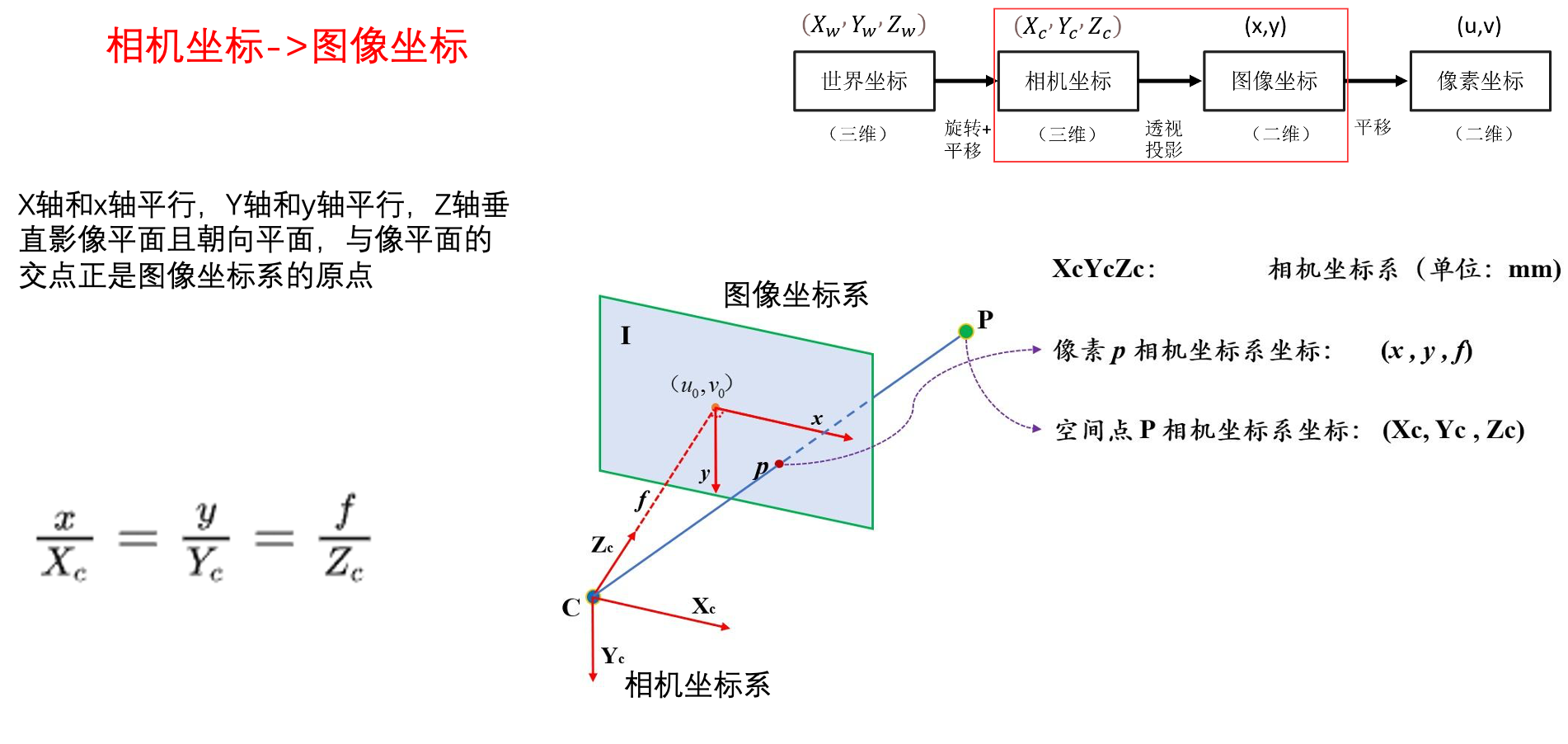
        三维到二维的转换，要先将它们的坐标都化为相机坐标系下的坐标，这里图像上的坐标化为相机坐标要借助焦距f（因为图像到相机坐标系的原点的垂直距离为f），故像素p在相机坐标系下的坐标为(x,y,f)，而空间点P在相机坐标系下的坐标为(X,Y,Z)。它们成比例关系。

         图像上任意像素点在相机坐标系下的坐标为(x,y,f)，（两个坐标系原点距离为焦距f），空间点的相机坐标系坐标为(X,Y,Z)，将线段CP和线段Cp投影到三个相机坐标轴，都是相似三角形，成比例的对应关系

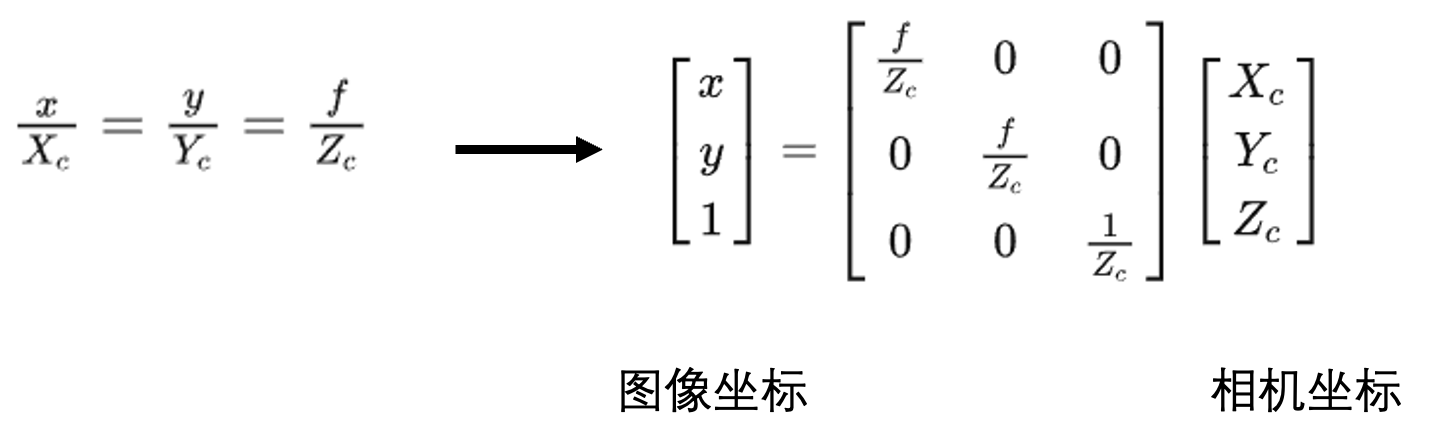
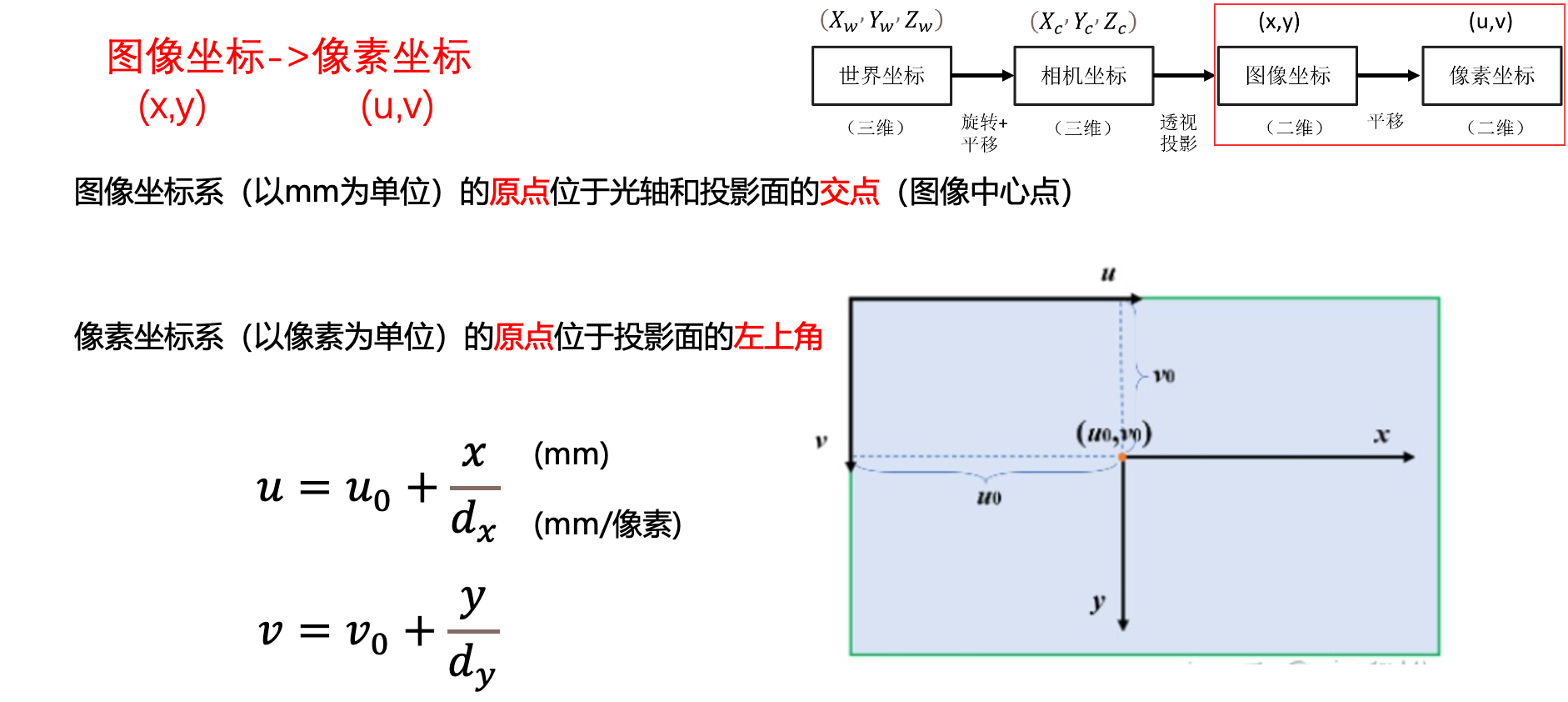
6、图像坐标->像素坐标

        图像坐标和像素坐标都是二维坐标，并且图像坐标和像素坐标的单位不一样，故它们之间的转换只需平移即可（平移的同时要进行单位换算）。

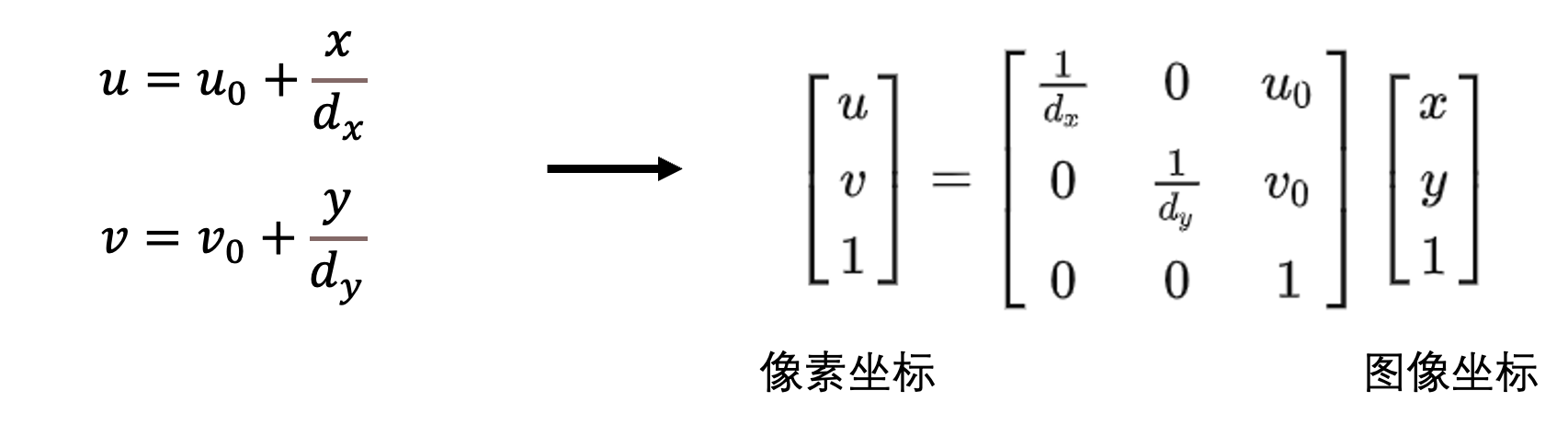
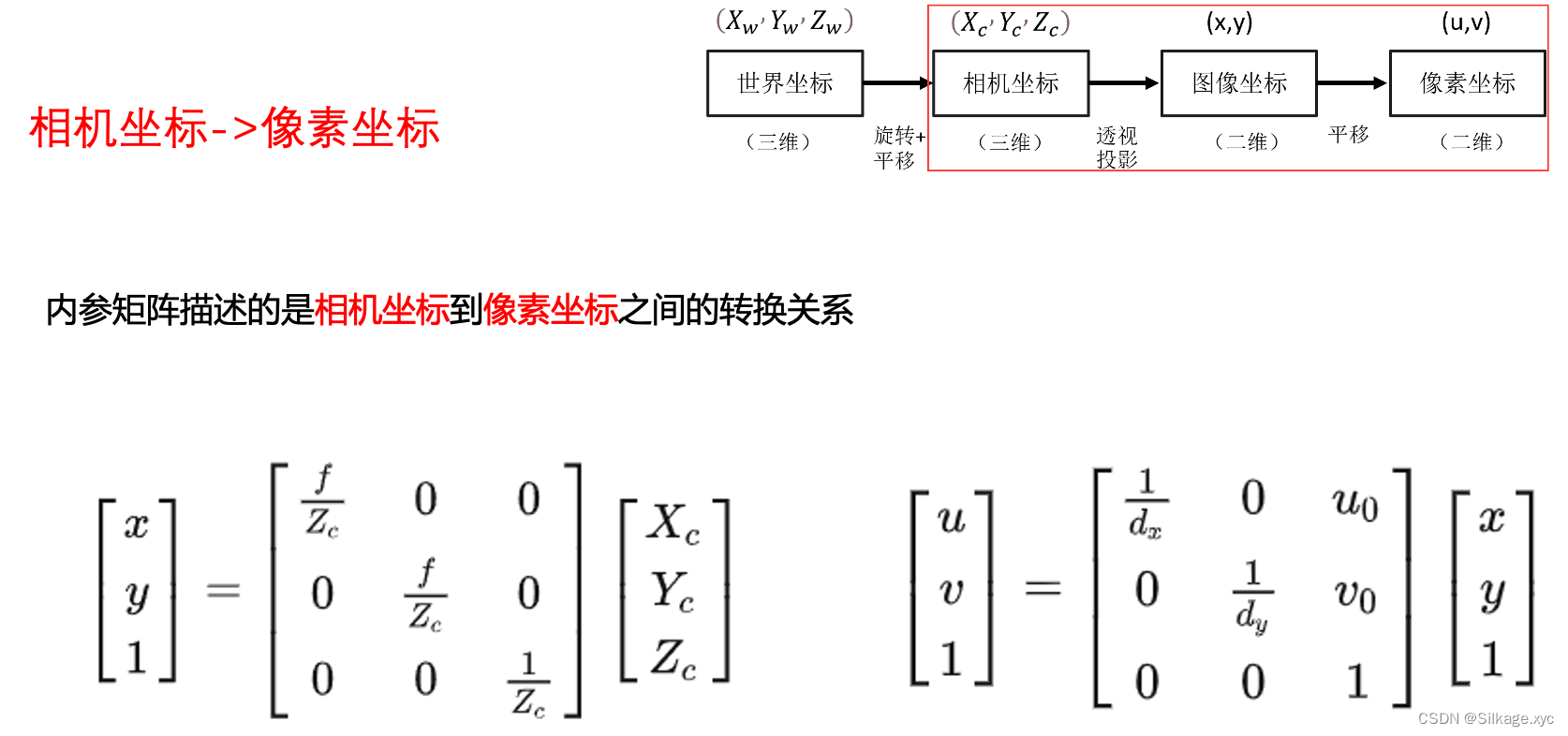
 7、内参

        相机坐标->像素坐标时需要使用内参矩阵，内参矩阵描述的是相机坐标到像素坐标之间的转换关系。

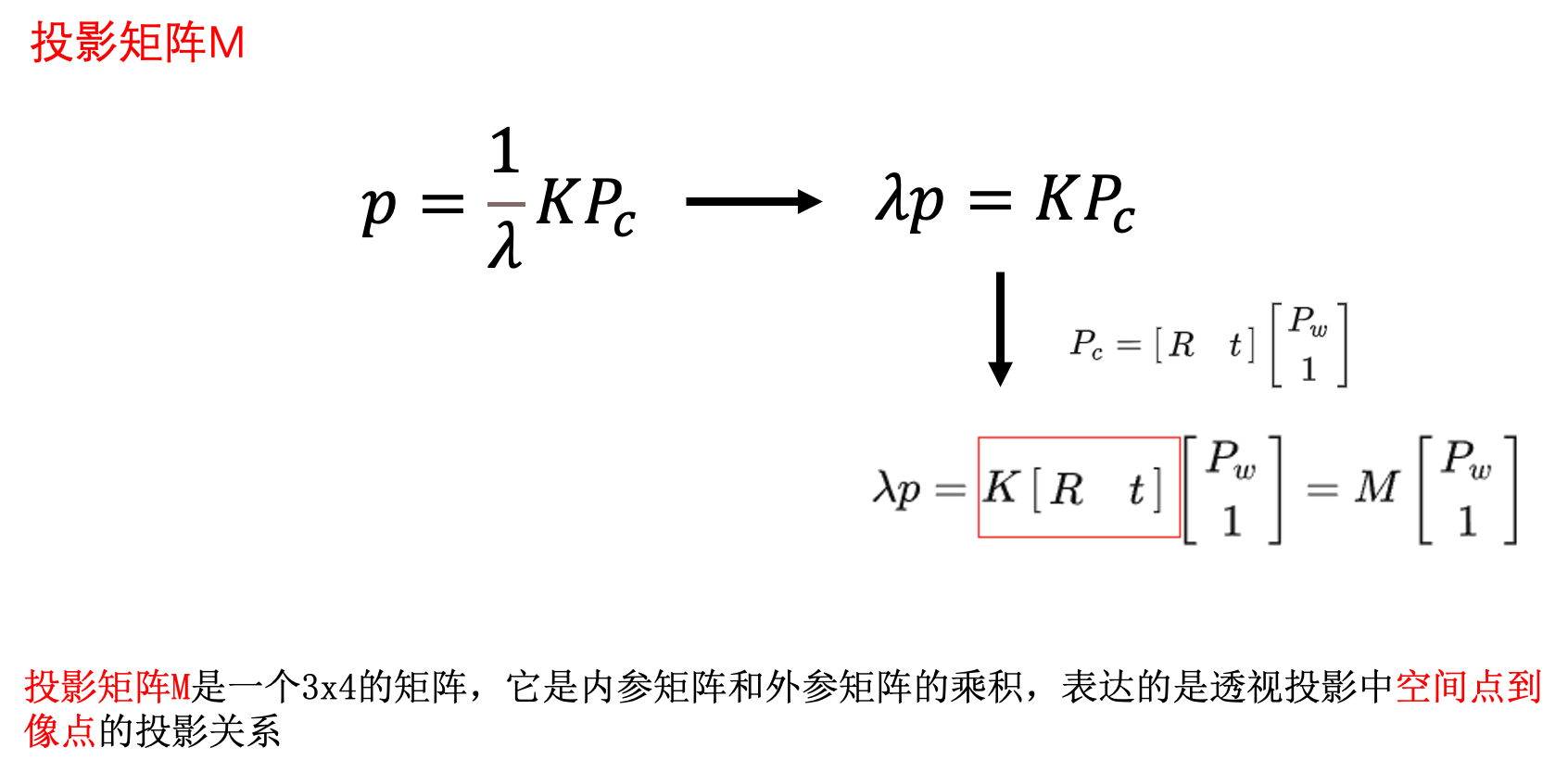
8、投影矩阵M

        投影矩阵M是一个3x4的矩阵，它是内参矩阵和外参矩阵的乘积，表达的是透视投影中空间点到像点的投影关系。