1018 Public Bike Management

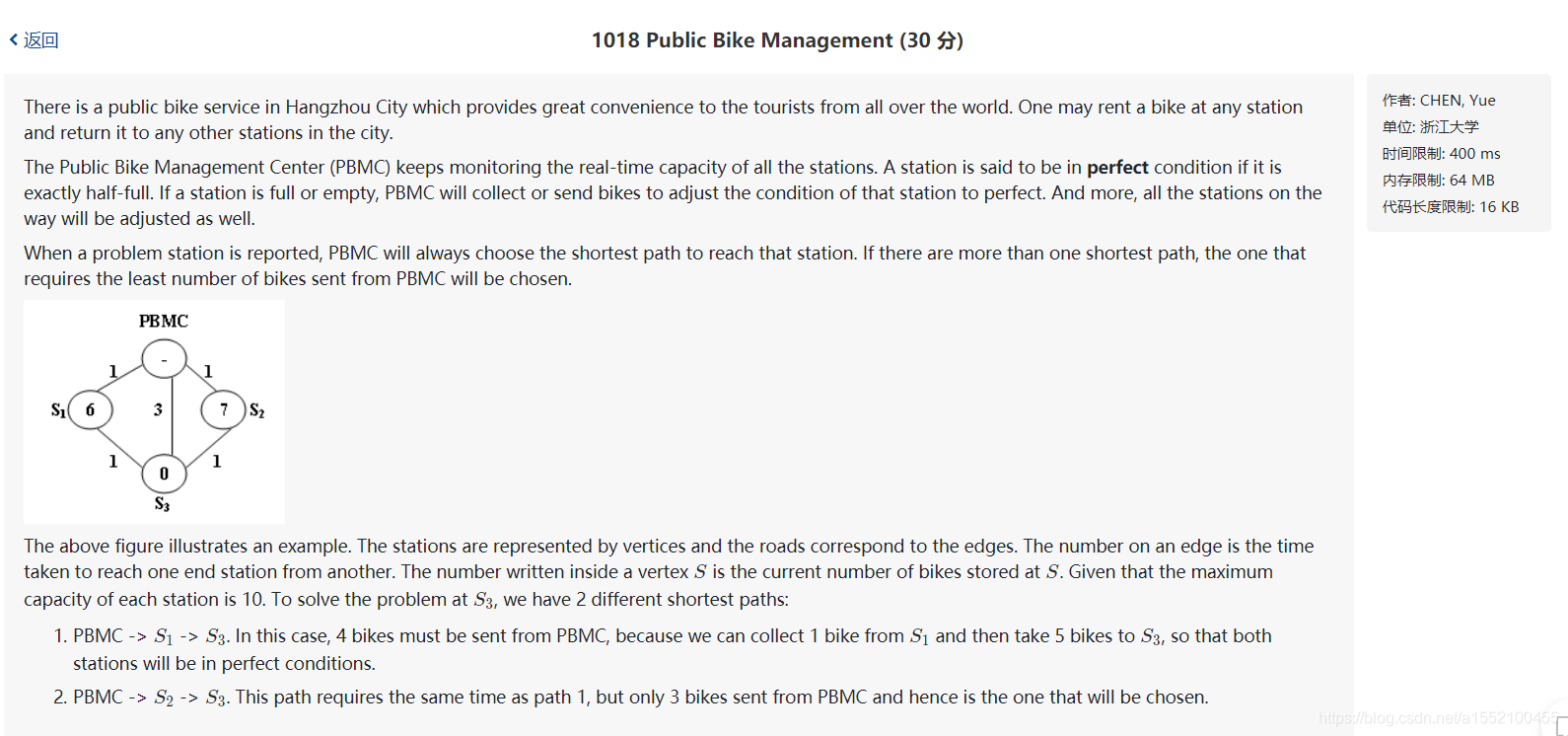
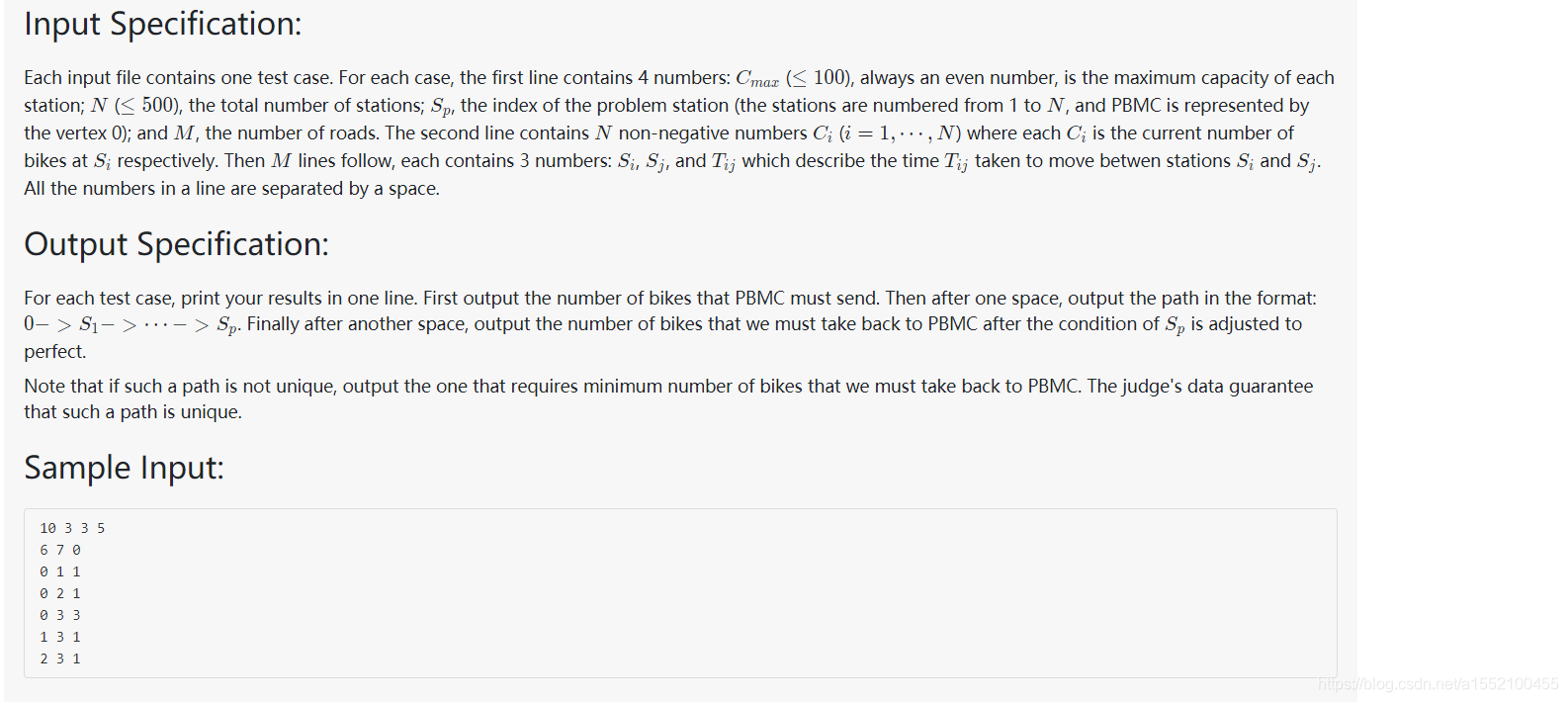
题目大意

一个车站里面自行车的数量恰好为c / 2，那么称处于完美状态。如果一个车站容量是满的或者空的，控制中心（处于结点0处）就会携带或者从路上收集一定数量的自行车前往该车站，一路上会让所有的车站沿途都达到完美。现在给出cmax，车站的数量n，问题车站sp，m条边，还有距离，求最短路径。如果最短路径有多个，求能带的最少的自行车数目的那条。如果还是有很多条不同的路，那么就选一条从车站带回的自行车数目最少的作为最终结果。

---

思路解析

一道最短路径的问题，首先存在多条路径，而且所有路径都要保存下来，所以path必然是一个二维数组。然后沿着path判断minSend和minBack。显然只有Dijkstra是不够的，需要加上深度优先，从每个路径的终点倒着遍历到控制中心，一路上统计back和send。每遍历完一条路径，要把这条路径记录下来，供输出使用。

---

示例代码

#include<iostream>
#include<vector>
#include<algorithm>
#define INF (~(0x1<<31))
using namespace std;
int c, n, sp, m, minBack = INF, minSend = INF;
int gra[501][501];
vector<vector<int>> path(501, vector<int>());//因为有多条路径，必须使用二维数组存储当前节点之前的多个pre节点
vector<int> tempath, finapath;//临时路径
vector<int> weight(501);//问题站点，角标为车站序列,元素为车站数目，正数表示需要送回的数量，负数表示需要补给的车辆
void dfs(int v) {
	tempath.push_back(v);
	if (v == 0) {//遍历到总部了
				 //从终点往起始点倒着统计
		int back = 0, send = 0;
		for (int i = tempath.size() - 1; i >= 0; i--) {
			int id = tempath[i];
			if (weight[id] > 0) {//表示需要送回
				back += weight[id];
			}
			else {//需要补给
				  //看看能否通过各站点匀一下
				if (back - abs(weight[id]) > 0) {//能匀
					back -= abs(weight[id]);//爽歪歪，直接不用往回送了
				}
				else {
					send += (abs(weight[id]) - back);
					back = 0;//都匀不过来了，更别提往回送了
				}
			}
		}
		if (send < minSend) {//统计最小值
			minSend = send;
			minBack = back;
			finapath = tempath;
		}
		else if (send == minSend && back < minBack) {
			minBack = back;
			finapath = tempath;
		}
		tempath.pop_back();//回溯 给兄弟节点留位置
		return;
	}
	for (int i = 0; i < path[v].size(); i++) {
		dfs(path[v][i]);
	}
	tempath.pop_back();//没有相连的节点了，要退回到上一步
}
int main() {
	scanf("%d%d%d%d", &c, &n, &sp, &m);
	int dist[501];
	fill(gra[0], gra[0] + 501 * 501, INF);
	fill(dist, dist + 501, INF);
	for (int i = 0; i < n; i++) {
		int temp;
		scanf("%d", &temp);
		weight[i + 1] = temp - c / 2;
	}
	for (int i = 0; i < m; i++) {
		int a, b, c;
		scanf("%d %d %d", &a, &b, &c);
		gra[a][b] = gra[b][a] = c;
	}
	vector<bool> visited(501, false);
	dist[0] = 0;
	for (int i = 0; i <= n; i++) {//不用初始化 上来就干
		int u, min = INF;
		for (int j = 0; j <= n; j++) {
			if (!visited[j] && dist[j] < min) {
				min = dist[j];
				u = j;
			}
		}
		visited[u] = true;
		for (int j = 0; j <= n; j++) {//更新最短路径
			if (!visited[j] && gra[u][j] != INF) {
				if (dist[u] + gra[u][j] < dist[j]) {//找到了新的最短路径
					path[j].clear();//之前储存的所有节点全部作废
					path[j].push_back(u);//新的前驱
					dist[j] = dist[u] + gra[u][j];
				}
				else if (dist[u] + gra[u][j] == dist[j]) {//路径长度相等 此时是多条路径
					path[j].push_back(u);
				}
			}
		}
	}
	dfs(sp);//从最后一个节点开始，个数就是序列
	printf("%d 0", minSend);//多输出一个0
	for (int i = finapath.size() - 2; i >= 0; i--) {
		printf("->%d", finapath[i]);
	}
	printf(" %d", minBack);
	return 0;
}