P9218 「TAOI-1」Apollo
题目描述
给出 n n n 个十进制小数 a 1 … a n a_1 \dots a_n a1…an。
对于一个 数 a a a,定义其精度 f ( a ) f(a) f(a) 表示最小的非负整数 k k k 使得 1 0 k × a 10^k\times a 10k×a 为整数;对于整数 a a a,定义 f ( a ) = 0 f(a) = 0 f(a)=0。对于两个十进制小数 a , b a, b a,b,定义 g ( a , b ) g(a, b) g(a,b) 为对于所有 数 c ∈ [ min ( a , b ) , max ( a , b ) ] c \in [\min(a,b), \max(a,b)] c∈[min(a,b),max(a,b)] 的 f ( c ) f(c) f(c) 的最小值。
对于所有 1 ≤ i ≤ n 1 \leq i \leq n 1≤i≤n,你需要求出 ∑ j = 1 n g ( a i , a j ) \sum\limits_{j=1}^ng(a_i, a_j) j=1∑ng(ai,aj) 的值并输出。
定义十进制小数是一个含有整数部分和小数部分的数,其小数部分不为 0 0 0。之所以描述得这么愚蠢是因为保证输入的每个数都有小数点,但是好像无论什么写法都会有人提出不满,真是抱歉了。
输入格式
第一行一个整数 n n n。
接下来 n n n 行,每行一个十进制小数 a i a_i ai。
输出格式
n n n 行,每行一个整数,分别表示 i = 1 … n i = 1 \dots n i=1…n 对应的答案。
输入输出样例 #1
输入 #1
5
11.4514
11.4778
11.1338
11.1236
11.4789
输出 #1
10
11
9
9
11
输入输出样例 #2
输入 #2
8
1.1145
1.114
1.1145
1.514
1.19198
1.1154
1.114
1.1145
输出 #2
24
21
24
10
18
22
21
24
说明/提示
数据范围
本题采用捆绑测试。
令 ∑ i = 1 n f ( a i ) = t \sum\limits_{i=1}^n f(a_i) = t i=1∑nf(ai)=t。
- Subtask 1(15 points): a i ≤ 10 a_i \leq 10 ai≤10, n ≤ 5 n \leq 5 n≤5, t ≤ 10 t \leq 10 t≤10。
- Subtask 2(15 points): a i ≤ 10 a_i \leq 10 ai≤10, n ≤ 100 n \leq 100 n≤100, t ≤ 1000 t \leq 1000 t≤1000。
- Subtask 3(20 points): n ≤ 1722 n \leq 1722 n≤1722。
- Subtask 4(15 points): a i ≤ 1 a_i \leq 1 ai≤1。
- Subtask 5(35 points):无特殊限制。
对于所有数据, 0 < a i < 1 0 9 0 \lt a_i \lt 10^9 0<ai<109, 1 ≤ n ≤ 1 0 5 1 \leq n \leq 10^5 1≤n≤105, 1 ≤ t ≤ 3 × 1 0 6 1 \leq t \leq 3 \times 10^6 1≤t≤3×106,保证 a i \bm{a_i} ai 没有后导 0 \color{black}\bm 0 0,不保证 a i \bm{a_i} ai 互不相同。
样例解释
以 i = 1 i = 1 i=1 为例:
- j = 1 j = 1 j=1:取 c = 11.4514 c = 11.4514 c=11.4514, f ( c ) = 4 f(c) = 4 f(c)=4;
- j = 2 j = 2 j=2:取 c = 11.46 c = 11.46 c=11.46, f ( c ) = 2 f(c) = 2 f(c)=2;
- j = 3 j = 3 j=3:取 c = 11.2 c = 11.2 c=11.2, f ( c ) = 1 f(c) = 1 f(c)=1;
- j = 4 j = 4 j=4:取 c = 11.3 c = 11.3 c=11.3, f ( c ) = 1 f(c) = 1 f(c)=1;
- j = 5 j = 5 j=5:取 c = 11.47 c = 11.47 c=11.47, f ( c ) = 2 f(c) = 2 f(c)=2。
故 ∑ j = 1 n g ( a 1 , a j ) = 4 + 2 + 1 + 1 + 2 = 10 \sum\limits_{j=1}^n g(a_1, a_j) = 4 + 2 + 1 + 1 + 2 = 10 j=1∑ng(a1,aj)=4+2+1+1+2=10。对于同一个 j j j,上文给出的所有 c c c,都可能有其它的不同的 c c c 满足 f ( c ) f(c) f(c) 同样最小。
题目分析
仔细阅读题目,可知题目要求的是对于每个 a i a_i ai 的 ∑ j = 1 n g ( a i , a j ) \sum\limits_{j=1}^ng(a_i,a_j) j=1∑ng(ai,aj) 。再结合 g ( a , b ) g(a,b) g(a,b) 的定义,可知,对于 a i a_i ai 来说,我们需要计算 a i a_i ai 与 a 1 ∼ a n a_1\sim a_n a1∼an 构成的 n n n 组数对的 g ( a i , a j ) g(a_i,a_j) g(ai,aj) 的总和。对于 g ( a , b ) g(a,b) g(a,b) 的值,则是 [ min ( a , b ) , max ( a , b ) ] [\min(a,b),\max(a,b)] [min(a,b),max(a,b)] 中的最小 f ( c ) f(c) f(c) 的值,当前 c ∈ [ min ( a , b ) , max ( a , b ) ] c\in [\min(a,b),\max(a,b)] c∈[min(a,b),max(a,b)]。对于 f ( c ) f(c) f(c) 的作用则是返回将小数 c c c 变成整数的乘 10 10 10 的次数,即 c c c 的小数部分的位数。题目描述的比较绕,需要耐心将公式之间的关系捋清楚。
接下来思考如何计算 g ( a , b ) g(a,b) g(a,b)。我们分情况进行讨论,为方便描述我们设 a ≤ b a\le b a≤b。
- 两个数的整数部分不同。
当整数部分不相同时,在 [ a , b ] [a,b] [a,b] 中一定可以存在一个整数 c c c ,当 c c c 为整数时, f ( c ) = 0 f(c)=0 f(c)=0。所以整数部分不相同, g ( a , b ) = 0 g(a,b)=0 g(a,b)=0。
-
两个数的整数部分相同。当整数部分相同时,考虑小数部分。可以分成三种情况:
-
小数部分完全不一样。
如 11.123 11.123 11.123 和 11.231 11.231 11.231 对应的 c = 11.2 c=11.2 c=11.2, f ( c ) = 1 f(c)=1 f(c)=1。也就是较小的数值保留1位小数再加 0.1 0.1 0.1 就好,这样乘 1 0 1 10^1 101 就能成为整数。
-
部分前缀相同。
如 11.12345 11.12345 11.12345 和 11.12388 11.12388 11.12388 对应的 c = 11.1235 c=11.1235 c=11.1235, f ( c ) = 4 f(c)=4 f(c)=4。也就是先找 a a a 和 b b b 的最大公共前缀,再往后一位,找一个在两者范围内的数字即可,若小数点后最大公共前缀长度为 k k k 则乘 1 0 k + 1 10^{k+1} 10k+1 就能成为整数。
-
较小的数字是较大数字的前缀。
如 11.123 11.123 11.123 和 11.123456 11.123456 11.123456 对应的 c = 11.123 c=11.123 c=11.123, f ( c ) = 3 f(c)=3 f(c)=3。也就是较小的那个数字的小数位数,若较小数字的小数位置为 k k k 则乘 1 0 k 10^k 10k 就能成为整数。
-
此时我们可以发现,问题是围绕着公共前缀展开的。对于小数的公共前缀,我们可以将小数视为字符串进行存储与使用,就将问题转换了字符串的公共前缀问题,这类问题使我们联想到字典树,可以考虑使用字典树解决它。
以样例2为例,讲解字典树解法思路。
8
1.1145
1.114
1.1145
1.514
1.19198
1.1154
1.114
1.1145
下图为建立好的字典树。
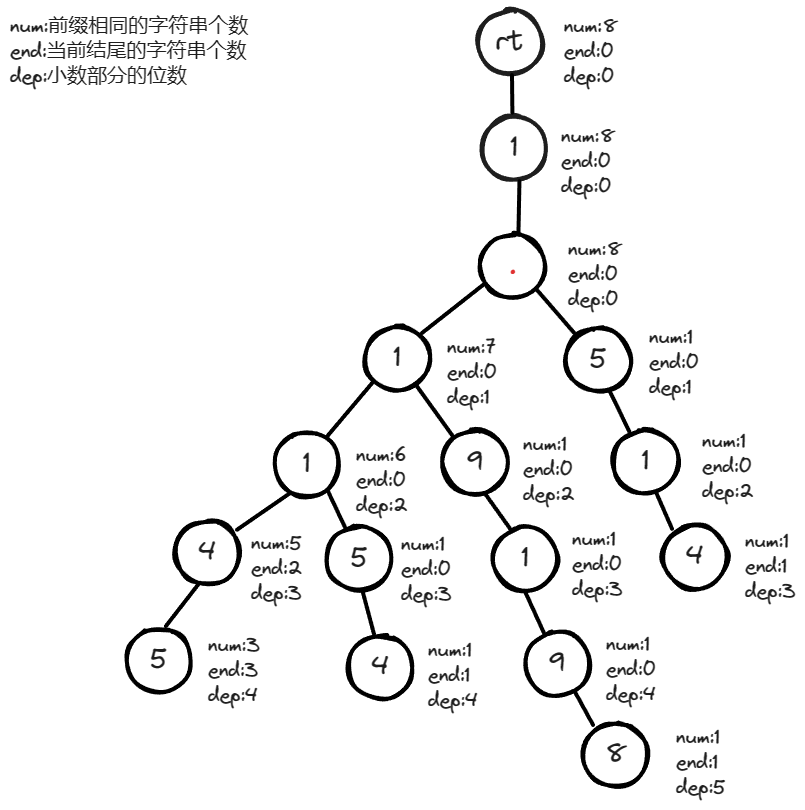
查找数值 1.1145 1.1145 1.1145 的答案过程。
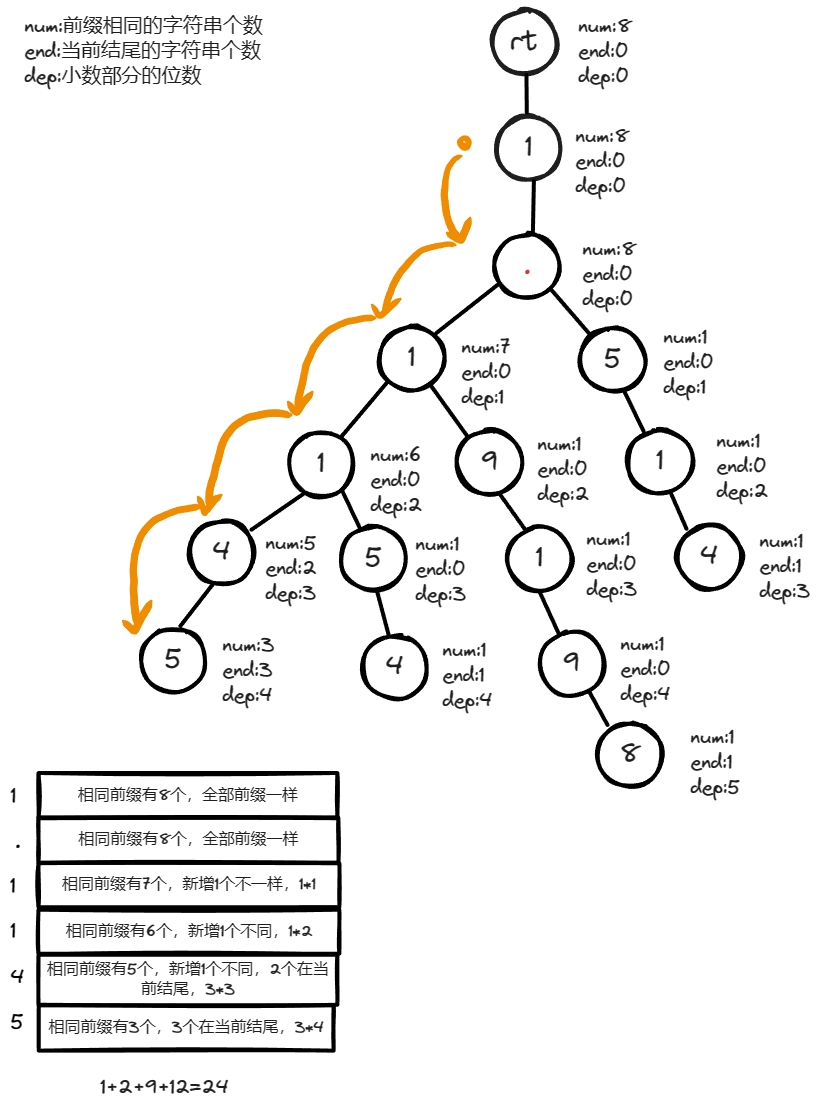
查找数值 1.114 1.114 1.114 的答案过程。
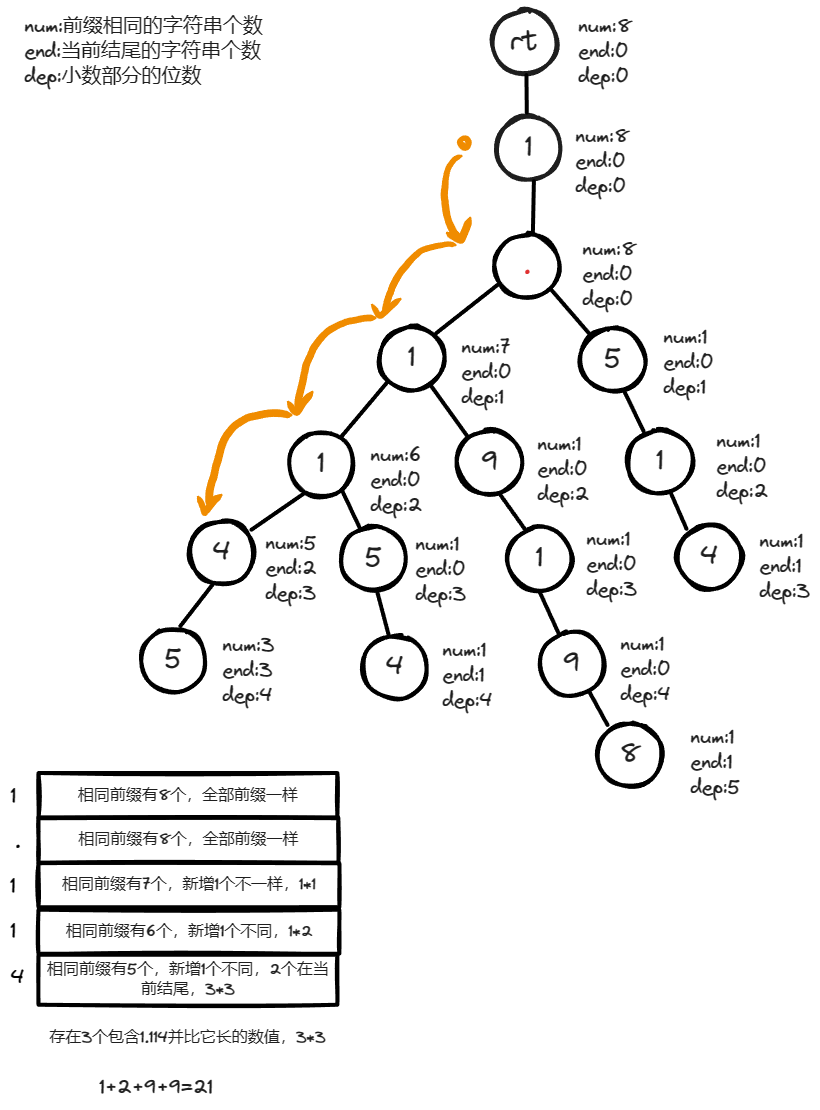
查找数值
1.514
1.514
1.514 的答案过程。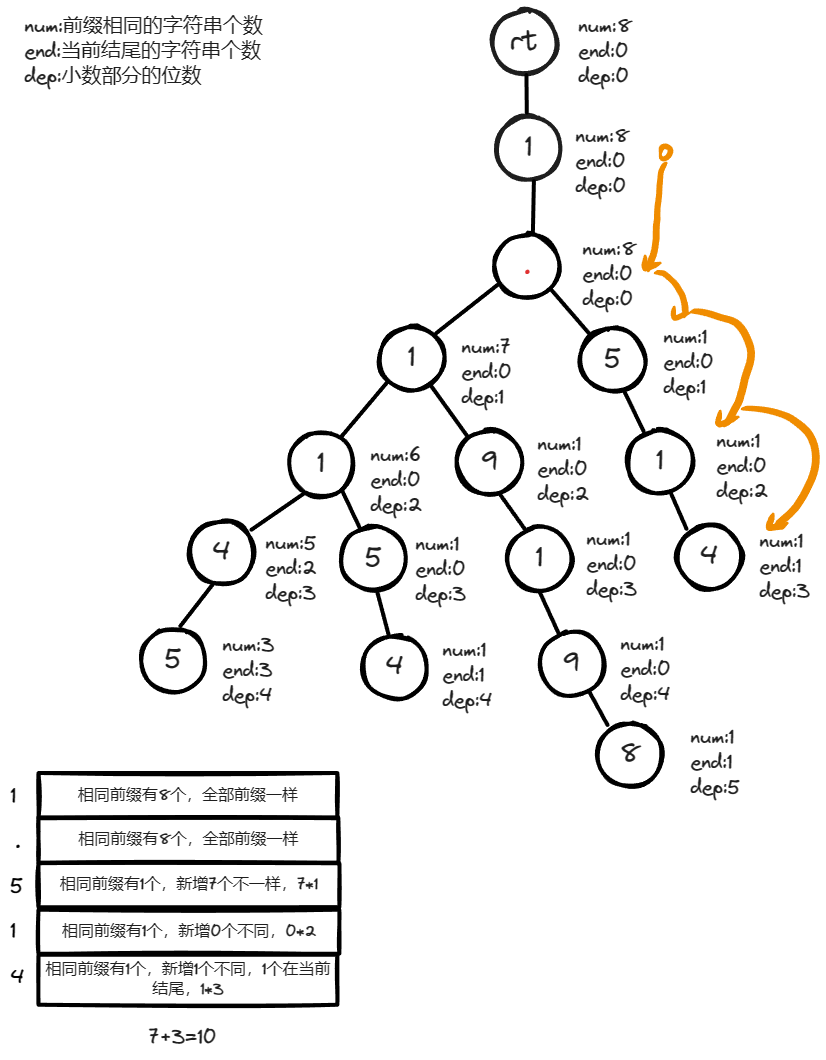
模拟过程中可发现,在遍历字典树的过程中,我们计算新增的不同前缀的元素个数与当前结尾的元素个数,它们成为整数的答案为当前小数位数。另外,在遍历结束后需要考虑和计算以当前数字为前缀且又比它长的数字个数,详细可查看寻找数值 1.114 1.114 1.114 的过程。
代码实现
#include <bits/stdc++.h>
using namespace std;
using i64 = long long;
const int N = 1e5 + 5;
const int M = 3e6 + 5;
int n, tot, zs;
string str[N];
struct node {
int son[11];
// 前缀相同的字符串个数、以该节点结尾的字符串个数、小数部分的位数
int num, end, dep;
} trie[M];
int toNum[256];
void init() {
for (int i = 0; i < 10; i++) {
toNum[i + '0'] = i;
}
toNum['.'] = 10;
}
void insert(string s) { // 字典树插入
int len = s.size();
int u = 0;
int dot = -1; // 小数点位置
trie[u].num++; // 记录字符串总数
for (int i = 0; i < len; i++) {
int ch = toNum[s[i]];
if (!trie[u].son[ch]) trie[u].son[ch] = ++tot;
u = trie[u].son[ch];
trie[u].num++;
if (ch == 10) dot = i; // 记录小数点的位置
if (dot != -1) trie[u].dep = i - dot; // 更新小数部分对应的位数
}
trie[u].end++;//记录该处结尾的数字个数
}
int findStr(string s) {
// 整数部分不一样,f(c)为0
// 整数部分相同时考虑小数部分的最大公共前缀
int len = s.size();
int sum = 0, re = trie[0].num; // re-剩余前缀相同的字符串数量
int u = 0;
for (int i = 0; i < len; i++) {
int ch = toNum[s[i]];
u = trie[u].son[ch];
// num=新增的前缀不同的字符串数量 + 以该节点结尾的字符串数量
int num = re - trie[u].num + trie[u].end;
sum += num * trie[u].dep; // 更新总和
re -= num;
}
// 处理前缀与s相同,但又比s长的字符串
sum += (trie[u].num - trie[u].end) * trie[u].dep;
return sum;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
init();
string s;
char c;
cin >> n;
for (int i = 1; i <= n; i++) {
cin >> str[i];
insert(str[i]);
}
for (int i = 1; i <= n; i++) {
cout << findStr(str[i]) << '\n';
}
return 0;
}





















 149
149

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








