动态规划——最长公共子序列

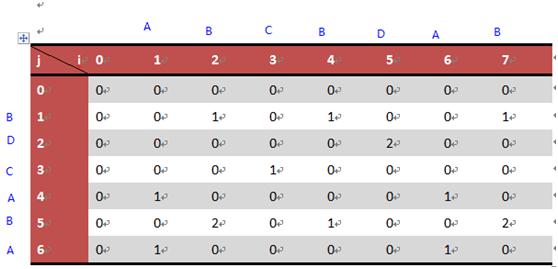
      两个序列的最长公共子序LCS(Longest Common Length)的每个字符可以不连续，如X=<A, B, C, B, D, A, B>，Y=<B, D, C, A, B, A>，那么它们的最长公共子序列为<B, C, B, A>。这是一个经典的动态规划问题，着手点还是找到最精髓的状态转移方程。假设X,Y两个序列的前i，j个位置的最大子序列已经找到为r[i][j](自底往上)，那么X[i] 与Y[j+1]的LCS就只要考虑一下两种情况：X[i] =Y[j+1] 和X[i] !=Y[j+1] ；若Xi=Yj ,那么最长公共序列为MaxLen(Xi-1 , Yj-1) + 1；若Xi !=Yj ,那么最长公共序列为MaxLen(Xi-1 ,Yj)和MaxLen(Xi ,Yj-1)中的最大值，具体如下：

根据下面的表格可以看出，每一列的数字最多增加1（当找到一个相同符号），一个字母只有当它前面的字母找到匹配时，它的增加才可能成为主路径。最后结果一定会累加到最后一个表格中

如果要寻找两个序列的最长公共子串，即连续相等的子序列，看起来有点麻烦，但只需将上面的状态方程X[i] !=Y[j]改为c[i,j]=0即可。

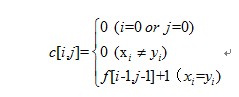
     这个图跟上面的图的区别就在于没有水平路径，只有斜对角线上相等的元素才能加1，其实就是要连续匹配的元素(i, j)与(i+1, j+1)才满足要求。

代码如下：

int LCS_dp(string a, string b, int l1, int l2)
{
	int r[100][100]={0};
	int len=0;
	int i,j;
	for(i=0; i<l1;i++)
	{
		for(j=0; j<l2; j++)
		{
			if(a[i] == b[j])
				r[i+1][j+1]=r[i][j]+1;
			else
				r[i+1][j+1]=max(r[i][j+1], r[i+1][j]);									
                        /*else 
				r[i+1][j+1]=0;	*/   //这个是求连续子串的状态方程，直接清零
			
			if(r[i+1][j+1] > len)  len=r[i+1][j+1];
		}
	}
	return len;																				
}