nyoj 1036-非洲小孩 (区间贪心)

最新推荐文章于 2019-04-10 19:57:00 发布

Suprit

最新推荐文章于 2019-04-10 19:57:00 发布

阅读量325

点赞数

CC 4.0 BY-SA版权

分类专栏： # 贪心

本文链接：https://blog.youkuaiyun.com/a1097304791/article/details/83386049

贪心专栏收录该内容

48 篇文章

订阅专栏

本文探讨了区间贪心问题中的区间选点问题，即如何选择最少的点覆盖所有给定区间，提出了两种解决策略：一是左端点排序后考虑右端点，二是右端点排序后考虑左端点，通过实例代码详细解析了两种算法的实现过程。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

http://nyoj.top/problem/1036

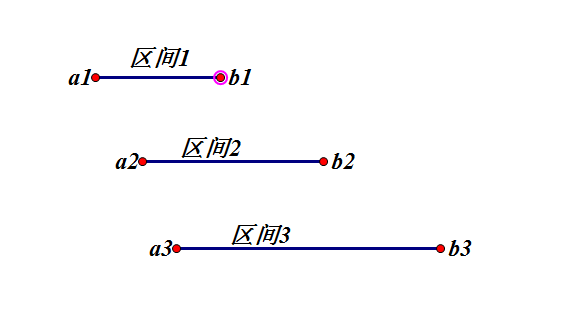
这是一道区间贪心问题中的区间选点问题, 即给定部分区间, 选得最少的点, 使得每个区间至少有一个点(含重叠)

应该来说有两种算法

一是左端点排序(<), 考虑右端点(<), 然后求交集的右边界, 没有交集就ans+1

//非洲的小孩 贪心
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
#include <string>
#include <vector>
#include <queue>
using namespace std;
#define ms(x, n) memset(x,n,sizeof(n));
typedef  long long LL;
const LL maxn = 110;
struct node{
    int b, e;
}t[maxn];
bool cmp(const node a, const node b)
{ //按开始时间升序排列, 如果相等按结束时间升序排列
    if(a.b==b.b) return a.e < b.e;
    return a.b < b.b;
}
int n;
int solve()
{
    sort(t+1, t+1+n, cmp);
    int ans = 1, range = t[1].e;
    for(int i = 2; i <= n; i++){
        if(t[i].b <= range) range = min(range, t[i].e);
        else range = t[i].e, ans++;
    }
    return ans;
}
int main()
{
    int h1,m1,h2,m2;
    while(cin >> n){
        ms(t, 0);
        for(int i = 1; i <= n; i++){
            scanf("%d:%d-%d:%d",&h1,&m1,&h2,&m2);
            t[i].b = h1*60+m1, t[i].e = h2*60+m2; //转化成分钟制
            if(t[i].b > t[i].e){ //考虑H1H1:M1M1晚于H2H2:M2M2的特殊情况
                swap(t[i].b, t[i].e);
            }
        }
        cout << solve() << endl;
    }
    return 0;
}

一种是右端点排序(<), 考虑左端点(>), 然后如果有交集就选可选区间的最后一个点, 没有交集就ans++

ç¤ºæå¾

//非洲的小孩 贪心
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
#include <string>
#include <vector>
#include <queue>
using namespace std;
#define ms(x, n) memset(x,n,sizeof(n));
typedef  long long LL;
const LL maxn = 110;
struct node{
    int b, e;
}t[maxn];
bool cmp(const node a, const node b)
{ //按开始时间升序排列, 如果相等按结束时间升序排列
    if(a.e==b.e) return a.b > b.b;
    return a.e < b.e;
}
int n;
int solve()
{
    sort(t+1, t+1+n, cmp);
    /*int ans = 1, range = t[1].e;
    for(int i = 2; i <= n; i++){
        if(t[i].b <= range) range = min(range, t[i].e);
        else range = t[i].e, ans++;
    }*/
    int ans = 0, cur = -10000;
    for(int i = 1; i <= n; i++)
        if(t[i].b > cur ) cur = t[i].e, ans++;
    return ans;
}
int main()
{
    int h1,m1,h2,m2;
    while(cin >> n){
        ms(t, 0);
        for(int i = 1; i <= n; i++){
            scanf("%d:%d-%d:%d",&h1,&m1,&h2,&m2);
            t[i].b = h1*60+m1, t[i].e = h2*60+m2; //转化成分钟制
            if(t[i].b > t[i].e){ //考虑H1H1:M1M1晚于H2H2:M2M2的特殊情况
                swap(t[i].b, t[i].e);
            }
        }
        cout << solve() << endl;
    }
    return 0;
}