母牛的故事 HDU - 2018 (递推 | 思维水题)

最新推荐文章于 2024-02-08 22:18:43 发布

Suprit

最新推荐文章于 2024-02-08 22:18:43 发布

阅读量1k

点赞数 1

CC 4.0 BY-SA版权

分类专栏： # 贪心 # 思维算法

本文链接：https://blog.youkuaiyun.com/a1097304791/article/details/83379232

思维算法同时被 2 个专栏收录

61 篇文章

订阅专栏

贪心

48 篇文章

订阅专栏

本文探讨了一道关于牛群数量增长的编程题目，通过分析题意找到了类似斐波那契数列的规律，即每年牛的数量等于前一年的数量加上前三年的数量，实现了递推算法的解决方案。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

https://vjudge.net/problem/HDU-2018

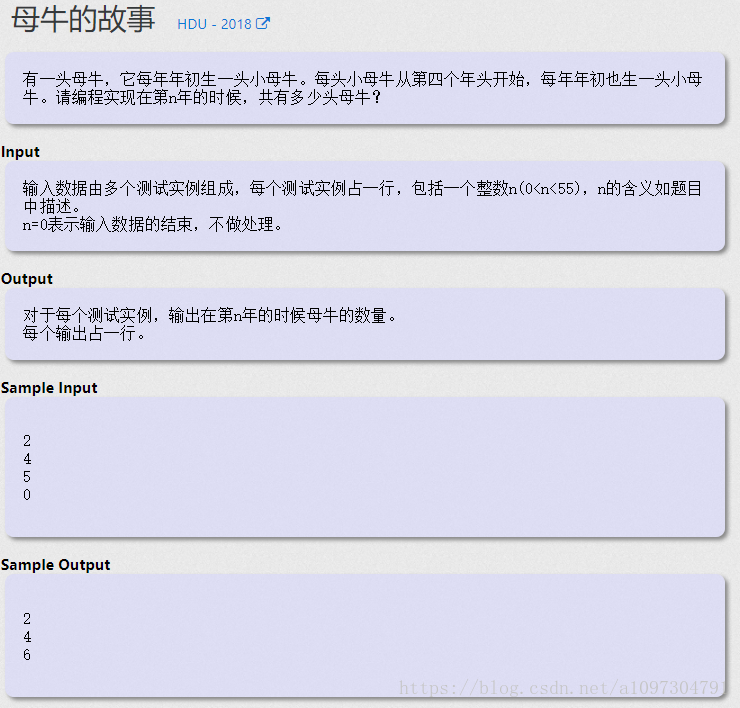
按理说这应该就是一道水题, 可最近实在对递推的理解有些生疏了, 考虑了很久一直在WA, 其实就是一个变种般的斐波那契数列

分析
　　根据题意，先列出前几年的牛头数，试着找找规律：

　　在列出这个序列的过程中，应当能找出规律。
　　以n=6为例，fn=9头牛可以分解为6+3，其中6是上一年（第5年）的牛，3是新生的牛（因为第3年有3头牛，这3头在第6年各生一头牛）。
　　我们可以得出这样一个公式：fn=fn-1+fn-3
　　再理解一下，fn-1是前一年的牛，第n年仍然在，fn-3是前三年那一年的牛，但换句话说也就是第n年具有生育能力的牛，也就是第n年能生下的小牛数。
　　编程序，求解这个公式就行了。
　　当然，第1-3年的数目，需要直接给出。
　　很像斐波那契数列，有不一样之处，道理、方法一样。其实，在编程之前，讲究先用这样的方式建模。

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;

const int maxn = 60;
int cows[maxn], n;
void solve(int m)
{
    memset(cows, 0, sizeof(cows));
    cows[1] = 1, cows[2] = 2, cows[3] = 3, cows[4] = 4;
    for(int i = 5; i <= m; i++)
        cows[i] = cows[i-1] + cows[i-3];
}
int main()
{
    solve(55);
    while(scanf("%d",&n) && n!=0)
        cout << cows[n] << endl;
    return 0;
}

参考: https://blog.youkuaiyun.com/sxhelijian/article/details/42609353