牛客练习赛32 ~ D ~ Where are you（kruskal + 边双联通）

题目链接

思路

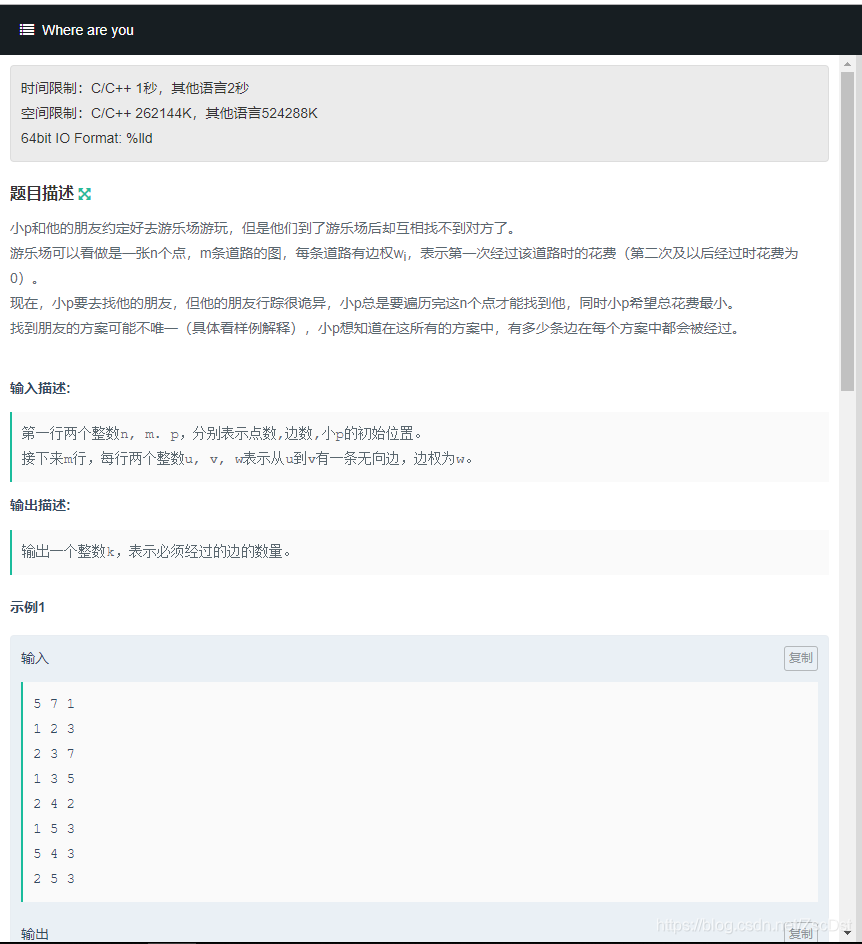
kruskal过程，我们按边权排序，然后依次加入，同时用并查集维护连通性。
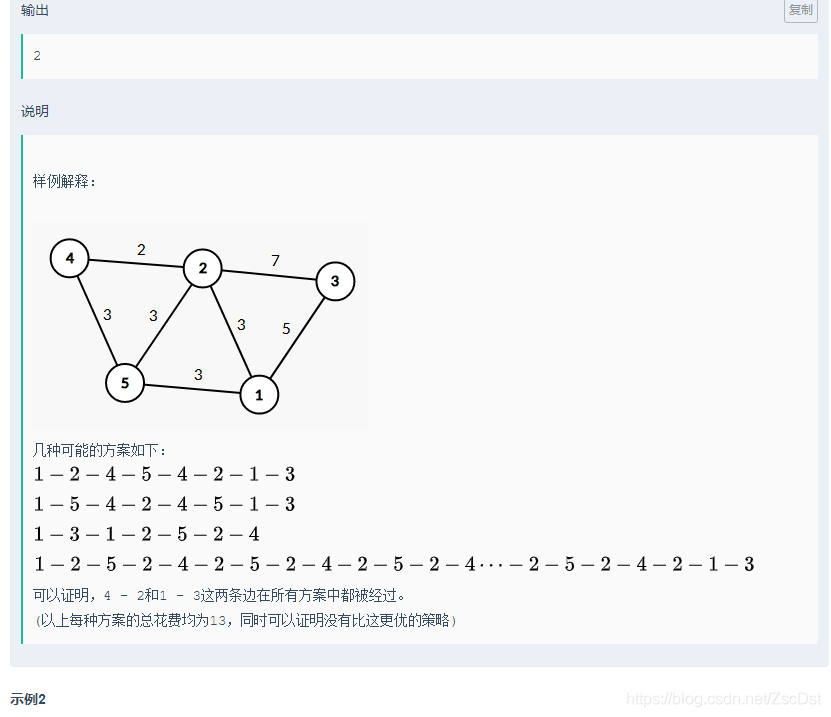
本题难以处理的其实是边权相同的边，我们把这些边一起考虑。假设此时最小生成树的这个森林中，我们把在一棵树（一个集合）看作一个点，以这些边权相同的边（如果这条边不太同一棵树中）建立新图，可以证明桥边一定必选。

#include <bits/stdc++.h>
using namespace std;
const int MAXN = 1e5 + 5;
const int MAXM = 1e5 + 5;
//边双连通分量
struct Edge
{
    int from, to;
    Edge(int u, int v) : from(u), to(v) {}
};
struct EdgeBCC//边双连通分量
{
    int n, m;
    int DFN[MAXN], LOW[MAXN], bccno[MAXN], dfs_clock, bcc_cnt;
    bool isbridge[MAXM];
    vector<Edge> edges;
    vector<int> G[MAXN], bridge;
    stack<int> S;

    void init(int n)
    {
        this->n = n, m = 0;
        edges.clear();
        for (int i = 0; i <= n; i++) G[i].clear();
    }

    void AddEdge (int from, int to)
    {
        edges.emplace_back(from, to);
        edges.emplace_back(to, from);
        m = edges.size();
        G[from].push_back(m - 2);
        G[to].push_back(m - 1);
    }

    void dfs(int u, int fa)
    {
        DFN[u] = LOW[u] = ++dfs_clock;
        S.push(u);
        for (auto id : G[u])
        {
            if ((id^1) == fa) continue;
            int v = edges[id].to;
            if (!DFN[v])
            {
                dfs(v, id);
                LOW[u] = min(LOW[u], LOW[v]);
                if (LOW[v] > DFN[u])//桥
                {
                    bridge.push_back(id);
                    isbridge[id] = isbridge[id^1] = true;
                }
            }
            else if (!bccno[v] && LOW[u] > DFN[v])
                LOW[u] = min(LOW[u], DFN[v]);
        }
        if (LOW[u] == DFN[u])
        {
            bcc_cnt++;
            while (1)
            {
                int x = S.top(); S.pop();
                bccno[x] = bcc_cnt;
                if (x == u) break;
            }
        }
    }

    void find_bcc()
    { // 注意点的编号从0开始, 连通分量的编号从1开始
        dfs_clock = bcc_cnt = 0;
        memset(DFN, 0, sizeof(DFN)), memset(bccno, 0, sizeof(bccno));
        bridge.clear(), memset(isbridge, 0, sizeof(isbridge));
        for (int i = 0; i < n; i++)
            if (!DFN[i]) dfs(i, -1);
    }

}EB;

struct EDGE
{
    int from, to, dist;       //起点,终点,边权
    EDGE () {}
    EDGE(int u, int v, int w) : from(u), to(v), dist(w) {}
};
struct Kruskal
{
    int n, m;            //点数,边数
    vector<EDGE> edges;  //边表
    int f[MAXN];         //并查集的父亲数组
    vector<int> res;     //生成树中的边的编号

    void init(int n)
    {
        this->n = n, m = 0;
        edges.clear(), res.clear();
        for (int i = 0; i <= n; i++) f[i] = i;
    }

    void AddEdge(int from, int to, int dist)
    {
        edges.push_back(EDGE(from, to, dist));
        m = edges.size();
    }

    int Find(int x) { return f[x] == x ? x : f[x] = Find(f[x]); } //并查集的Find

    int kruskal(int& x)
    {
        int ans = 0;
        sort(edges.begin(), edges.end(),
             [](const EDGE& a, const EDGE& b){ return a.dist < b.dist; });

        for (int i = 0; i < m; )
        {
            int j = i;
            while (j < m && edges[i].dist == edges[j].dist) j++;
            EB.init(n);
            for (int k = i; k < j; k++)
            {
                EDGE& e = edges[k];
                int root1 = Find(e.from), root2 = Find(e.to);
                if (root1 != root2)
                {
                    EB.AddEdge(root1, root2);
                }
            }
            EB.find_bcc();
            x += EB.bridge.size();
            for (int k = i; k < j; k++)
            {
                EDGE& e = edges[k];
                int root1 = Find(e.from), root2 = Find(e.to);
                if (root1 != root2)
                {
                    f[root1] = root2;
                    ans += e.dist;
                    res.push_back(k);
                }
            }
            i = j;
            if (res.size() == n-1) break;
        }
        return ans;
    }

}gao;

int main()
{
    int n, m, p; scanf("%d%d%d", &n, &m, &p);
    gao.init(n);
    while (m--)
    {
        int u, v, w; scanf("%d%d%d", &u, &v, &w);
        u--, v--;
        gao.AddEdge(u, v, w);
    }
    int ans = 0;
    gao.kruskal(ans);
    printf("%d\n", ans);
    return 0;
}
/*
5 7 1
1 2 3
2 3 7
1 3 5
2 4 2
1 5 3
5 4 3
2 5 3
*/