机器学习科普以及经典算法介绍

人工智能的了解

1. 原理
2. 适用范围：数据要是什么分布，此算法使用于哪些范围
3. 哪些应用
4. 相类似的其他方法

1. 什么是人工智能

人类智慧是人类的“隐性智慧”与“显性智慧”相互作用相互促进相辅相成的能力体系。其中，“隐性智慧”主要是指人类发现问题、定义问题、解决问题的能力，由目的、知识、直觉能力、抽象能力、想象能力、灵感能力、顿悟能力和艺术创造能力所支持，具有很强的内隐性，因而不容易被确切理解，更难以在机器上进行模拟；“显性智慧”主要是指人类在隐性智慧所设定工作框架内解决问题的能力，依赖于收集信息、生成知识和创生解决问题的策略并转换为行动等能力的支持，而人工智能目前只做到了解决问题的程度。

1. 人工智能的历史

1. 人工智能的目标

知识表示和推理：命题演算和归结，谓词演算和归结，可以进行一些公式或定理的推导。知识图谱

一个知识工程的底层技术架构

博弈和伦理/自动规划包括机器人的计划、动作和学习，状态空间搜索，敌对搜索，规划等内容。

机器学习这一研究领域是由AI的一个子目标发展而来，用来帮助机器和软件进行自我学习来解决遇到的问题。机器学习的方式包括：有监督学习、无监督学习、半监督学习和强化学习。其中的算法有：回归算法（最小二乘法、LR等），基于实例的算法（KNN、LVQ等），正则化方法（LASSO等），决策树算法（CART、C4.5、RF等），贝叶斯方法（朴素贝叶斯、BBN等），基于核的算法（SVM、LDA等），聚类算法（K-Means、DBSCAN、EM等），关联规则（Apriori、FP-Grouth），遗传算法，人工神经网络（PNN、BP等），深度学习（RBN、DBN、CNN、DNN、LSTM、GAN等），降维方法（PCA、PLS等），集成方法（Boosting、Bagging、AdaBoost、RF、GBDT等）  《机器学习知识表格》和《机器学习方法汇总》。《一文读懂深度学习》

自然语言处理是另一个由AI的一个子目标发展而来的研究领域，用来帮助机器与真人进行沟通交流。

计算机视觉是由AI的目标而兴起的一个领域，用来辨认和识别机器所能看到的物体。

机器人学也是脱胎于AI的目标，用来给一个机器赋予实际的形态以完成实际的动作。

1. 人工智能、机器学习、数据挖掘的关系

人工智能是一个很大的研究领域；机器学习是人工智能的一个目标，提供很多算法；而数据挖掘是偏向算法应用的部分。

机器学习：是这样的领域，赋予计算机学习的能力，但这种能力不是通过显著式编程获得的。

1. 显著式编程：有固定的规定输入和输出
2. 非显著式编程：我们规定了行为和收益函数后，让计算机自己去找最大化收益函数的行为。（能够通过数据和经验自己学习，完成人类交给的任务）

一个计算机程序被称为可以学习，是指它能够针对某个任务T和某个性能指标P，从经验E中学习。这种学习的特点是，它在T上的被P所衡量的性能，会随着经验E的增加而提高

 

1. 机器学习的分类

监督学习（Supervised Learning）：人为输入计算机训练样本以及加上对应的标签的行为。根据数据标签存在与否分为

1. 传统的监督学习（Traditional Supervised Learning）：都有对应的标签

• 支持向量机（Support Vector Machine）
• 人工神经网络（Neural Networks）
• 深度学习网络（Deep Neural Networks）

1. 非监督学习（Unsupervised Learning）：所有的训练数据都没有对应的标签（同一类的数据在标签中距离更近来分类）

• 聚类（Clustering）
• EM算法(Expectation-Maximization algorithm)
• 主成分分析(Principle Component Analysis)

1. 半监督学习（Semi-supervised Learning）:训练数据中一部分有标签，一部分没有标签（如何应用少量的标注数据和大量的未标注数据去训练一个更好的机器学习算法）

 

强化学习（Reinforcement Learning）：计算机通过与环境的互动逐渐强化自己的行为模式

机器学习算法过程

本质：在有限的已知数据以及复杂的高维特征空间中预测未知的样本

1. 特征提取(Feature Extraction)：通过训练样本获得的，对机器学习任务有帮助的多维度数据
2. 特征选择(Feature Selection)
3. 不同的场景下应该获得的机器学习算法：没有免费午餐定理：任何一个预测函数，如果在一些训练样本表现好，那么必然在另一些训练样本上表现不好，如果不对数据在特征空间的先验分布有一定的假设，那么所有算法的表现将是一样的。
4. 研究新的机器学习算法以便适应新的场景

 

机器学习十大经典算法

1. 线性回归(Linear Regression)

1.1概念：

一种通过属性的线性组合来进行预测的线性模型，最终的目的是找出一条直线来对数据进行拟合，使得预测值和真实值的误差最小。

1.2特点

优点：结果具有很好的可解释性（w直观表达了各属性在预测中的重要性，计算熵不复杂。

缺点：对非线性数据拟合不好。

适用数据类型：数值型和标称型数据

简单用途：可以用来进行房价收入等的预测。

1.3模型表达

建立数学模型前，我们先定义如下变量：

1. Xi表示输入数据(future)
2. Yi表示输出数据(target)
3. (Xi, Yi)表示一组训练数据(training example)
4. m表示训练数据的个数
5. n表示特征数量

回归分析属于监督学习（利用已有的数据X，和数据的标注Y，找到x和y之间的对应关系），而监督学习的目标便是根据给定的训练数据，可以得到函数方法。对于线性回归而言，

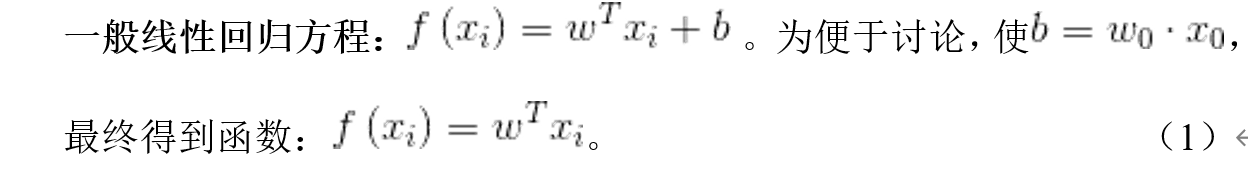
预测值和真实值之间的关系：对于每个样本，存在误差 ：

                                                                （2）

为了我们方便使用矩阵来表达，我们希望找出一组w，使得 无限接近于0，此处我们引入梯度下降算法解决问题。

1. 1. 梯度下降算法
2. 梯度下降算法的描述

实际生活中，有时我们也利用此算法，比如我们处在一座山的某处位置，但我们并不知道如何下山，于是走一步算一步，但每次都沿着最陡峭的地点下山，即沿着梯度的负方向。然而，并不是每次都达到山脚，也有可能到达山峰的某个局部最低点，即不一定得到全局最优解，也有可能是局部最优解。在此问题中，因为求解的函数是凸函数，所以得到的解一定是全局最优解。

1. 梯度下降算法的相关概念

1. 步长(Learning Rate)：决定沿着梯度负方向前进的长度
2. 特征(Feature)：即上述描述的Xi, Yi
3. 假设函数(Hypothesis Function)：在监督学习中，为了拟合输入样本，而使用f(xi)
4. 损失函数(Loss Function):为了评估模型拟合的好坏。损失函数越小，意味着拟合的程度越好，对应的模型参数即为最优参数。

1. 梯度下降算法的求解过程

2. 

（小tips：引入似然函数是为了根据样本估计参数值。

对于极大似然估计采取的步骤：写出似然函数；如果无法直接求导的话，对似然函数取对数，将乘法转化为加法，简化计算；求导数，令导数为0，得到似然方程；解似然方程，得到的参数即为所求）                           

          （6）

1. 求损失函数：

   （7）（最小二乘法）

（小tips：为什么要让损失函数越小越好：似然函数表示样本成为真实的概率，似然函数越大越好，也就是损失函数越小越好。其实就是(预测值-真实值)的平法和的平均值，换句话说就是点到直线距离和最小。）

1. 求权重参数w：求偏导：

                  

1. 线性回归模型

1. 1. 实际应用
2. 描述

从给定的房屋基本信息以及房屋销售信息等，建立一个回归模型预测房屋的销售价格。  测试数据主要包括3000条记录，13个字段，跟训练数据的不同是测试数据并不包括房屋销售价格。我们所要求的就是通过由训练数据所建立的模型以及所给的测试数据，得出测试数据相应的房屋销售价格预测值。

数据字段说明：

第一列“销售日期”：2014年5月到2015年5月房屋出售时的日期

第二列“销售价格”：房屋交易价格，单位为美元，是目标预测值

第三列“卧室数”：房屋中的卧室数目

第四列“浴室数”：房屋中的浴室数目

第五列“房屋面积”：房屋里的生活面积

第六列“停车面积”：停车坪的面积

第七列“楼层数”：房屋的楼层数

第八列“房屋评分”：King County房屋评分系统对房屋的总体评分

第九列“建筑面积”：除了地下室之外的房屋建筑面积

第十列“地下室面积”：地下室的面积

第十一列“建筑年份”：房屋建成的年份

第十二列“修复年份”：房屋上次修复的年份

第十三列"纬度"：房屋所在纬度 第十四列“经度”：房屋所在经度

1. 数据处理

 

1. 代码
2. 
   from __future__ import print_function
   
   # 导入相关python库
   import os
   import numpy as np
   import pandas as pd
   
   # 设定随机数种子
   np.random.seed(36)
   
   # 使用matplotlib库画图
   import matplotlib
   import seaborn
   import matplotlib.pyplot as plot
   
   from sklearn import datasets
   
   # 读取数据
   housing = pd.read_csv('kc_train.csv')
   target = pd.read_csv('kc_train2.csv')  # 销售价格
   t = pd.read_csv('kc_test.csv')  # 测试数据
   
   # 数据预处理
   housing.info()  # 查看是否有缺失值
   
   # 特征缩放
   from sklearn.preprocessing import MinMaxScaler
   
   minmax_scaler = MinMaxScaler()
   minmax_scaler.fit(housing)  # 进行内部拟合，内部参数会发生变化
   scaler_housing = minmax_scaler.transform(housing)
   scaler_housing = pd.DataFrame(scaler_housing, columns=housing.columns)
   
   mm = MinMaxScaler()
   mm.fit(t)
   scaler_t = mm.transform(t)
   scaler_t = pd.DataFrame(scaler_t, columns=t.columns)
   
   # 选择基于梯度下降的线性回归模型
   from sklearn.linear_model import LinearRegression
   
   LR_reg = LinearRegression()
   # 进行拟合
   LR_reg.fit(scaler_housing, target)
   
   # 使用均方误差用于评价模型好坏
   from sklearn.metrics import mean_squared_error
   
   preds = LR_reg.predict(scaler_housing)  # 输入数据进行预测得到结果
   mse = mean_squared_error(preds, target)  # 使用均方误差来评价模型好坏，可以输出mse进行查看评价值
   
   # 绘图进行比较
   plot.figure(figsize=(10, 7))  # 画布大小
   num = 100
   x = np.arange(1, num + 1)  # 取100个点进行比较
   plot.plot(x, target[:num], label='target')  # 目标取值
   plot.plot(x, preds[:num], label='preds')  # 预测取值
   plot.legend(loc='upper right')  # 线条显示位置
   plot.show()
   
   # 输出测试数据
   result = LR_reg.predict(scaler_t)
   df_result = pd.DataFrame(result)
   df_result.to_csv("result.csv")

   

3. 逻辑回归（Logistic Regression）

2.1 概念

一种广义线性回归，即在线性回归的基础上，我们将假设值和概率结合得到分类器，从而达到分类的效果。常用于分类。具体公式如

其中，(2)被称作sigmoid函数，我们可以看到，Logistic Regression算法是将线性函数的结果映射到了sigmoid函数中。接下来引入sigmoid函数。

2.2 sigmoid 函数

1. 概念

作为激活函数用于隐层神经元输出，取值范围为(0,1)，可以用来做二分类。Sigmoid作为激活函数有以下优缺点：

优点：平滑、易于求导。

缺点：激活函数计算量大，反向传播求误差梯度时，求导涉及除法；反向传播时，很容易就会出现梯度消失的情况，从而无法完成深层网络的训练。

1. 性质
   1. 1. 函数连续且单调递增
      2. 函数关于（0,0.5）对称
      3. x∈(−∞,∞)时y∈(0,1)
2. 代码

#plot sigmoid function

import numpy as np

import matplotlib.pyplot as plt



##sigmoid function

x=np.arange(-5,5,0.1)

y=1/(1+np.exp(-x))



#plot

plt.figure()

plt.plot(x,y,color='red',linewidth='2')

ax=plt.gca()

ax.spines['right'].set_color('none')

ax.spines['top'].set_color('none')

ax.xaxis.set_ticks_position('bottom')

ax.spines['bottom'].set_position(('data',0))

ax.yaxis.set_ticks_position('left')

ax.spines['left'].set_position(('data',0))

plt.xlabel('independent variable')

plt.ylabel('dependent variable')

plt.show()

2.3 原理推导

将sigmoid函数看成样本数据的概率密度函数。根据2.1，接下来需要做的就是怎样去估计参数 θ。

1. 根据条件概率，即hθ(x)结果取1/0的概率,可得

 

1. 极大似然估计

1. 梯度下降算法求θ

首先乘上-1/m，所以J（θ）最小时θ为最佳参数

算法复杂度为O(kn2)，n为特征数量，当求得一组θ时我们便能得到逻辑回归函数

1. 1. 回归实现

import numpy as np

import matplotlib.pyplot as plt

from matplotlib.colors import ListedColormap

from sklearn import datasets

from sklearn.model_selection import train_test_split

from sklearn.linear_model import LogisticRegression

from sklearn.preprocessing import StandardScaler



def plot_decision_regions(X, y, classifier, test_idx=None, resolution=0.02):

    # setup marker generator and color map

    markers = ('s', 'x', 'o', '^', 'v')

    colors = ('red', 'blue', 'lightgreen', 'cyan', 'gray')

    cmap = ListedColormap(colors[:len(np.unique(y))])

    # plot the decision surface

    x1_min, x1_max = X[:, 0].min() - 1, X[:, 0].max() + 1

    x2_min, x2_max = X[:, 1].min() - 1, X[:, 1].max() + 1

    xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, resolution), np.arange(x2_min, x2_max, resolution))

    Z = classifier.predict(np.array([xx1.ravel(), xx2.ravel()]).T)

    Z = Z.reshape(xx1.shape)

    plt.contourf(xx1, xx2, Z, alpha=0.4, cmap=cmap)

    plt.xlim(xx1.min(), xx1.max())

    plt.ylim(xx2.min(), xx2.max())

    # plot class samples

    for idx, cl in enumerate(np.unique(y)):

        plt.scatter(x=X[y == cl, 0], y=X[y == cl, 1],alpha=0.8, c=cmap(idx),marker=markers[idx], label=cl)

    # highlight test samples

    if test_idx:

        X_test, y_test = X[test_idx, :], y[test_idx]

        plt.scatter(X_test[:, 0], X_test[:, 1], c='blue', alpha=1.0, linewidth=1, marker='o', s=55, label='test set')



iris = datasets.load_iris()

X = iris.data[:, [2, 3]]

y = iris.target

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)

#为了追求机器学习的最佳性能，我们将特征缩放

sc = StandardScaler()

sc.fit(X_train)#估算每个特征的平均值和标准差

X_train_std=sc.transform(X_train)#用同样的参数来标准化测试集，使得测试集和训练集之间有可比性

X_test_std=sc.transform(X_test)

X_combined_std = np.vstack((X_train_std, X_test_std))

y_combined = np.hstack((y_train, y_test))



#训练感知机模型

lr = LogisticRegression(C=1000.0,random_state=0)#迭代次数为1000次,random_state设置随机种子，每次迭代都有相同的训练集顺序

lr.fit(X_train_std, y_train)

lr.predict_proba(X_test_std)



#绘图

plot_decision_regions(X_combined_std, y_combined, classifier=lr, test_idx=range(105,150))

plt.xlabel('petal length [standardized]')

plt.ylabel('petal width [standardized]')

plt.legend(loc='upper left')

plt.show()

2.5 逻辑回归和线性回归的区别

线性回归用来做预测,LR用来做分类。

线性回归是来拟合函数,LR是来预测函数。

线性回归用最小二乘法来计算参数。LR用最大似然估计来计算参数。

线性回归更容易受到异常值的影响,而LR对异常值有较好的稳定性。

 

1. 朴素贝叶斯（Naive Bayes）

3.1 概念

能够根据数据加先验概率来估计后验概率，在垃圾邮件分类、文本分类、信用等级评定等多分类问题中得到广泛应用。对于多数的分类算法，比如决策树、KNN等，他们都是判别方法，也就是直接学习得到特征输出Y和特征X之间的关系。但朴素贝叶斯和多数分类算法都不同，朴素贝叶斯是生成算法，也就是先找出特征输出Y和特征X的联合分布P(X,Y) ，然后用P(Y|X)=P(X,Y)P(X)得出

 

奥卡姆剃刀：实际生活中，越常见的越好

3.2特点

训练容易，推理难

1. 优点

1. 具有稳定的分类效率。
2. 对缺失数据不敏感，算法也比较简单。
3. 对小规模数据表现良好，能处理多分类任务，适合增量式训练。尤其是数据量超出内存后，我们可以一批批的去增量训练。
4. 简单易懂、学习效率高，在某些领域的分类问题中能够与决策树相媲美

1. 缺点

1. 对输入数据的表达形式比较敏感，需针对不同类型数据采用不同模型。
2. 由于我们是使用数据加先验概率预测后验概率，所以分类决策存在一定的错误率。
3. 假设各特征之间相互独立，但实际生活中往往不成立，因此对特征个数比较多或特征之间相关性比较大的数据来说，分类效果可能不是太好。
4. 以自变量之间的独立性和连续变量的正态性假设为前提，会导致算法精度在一定程度上受到影响。

3.3统计知识回顾

1. 

   

3.4朴素贝叶斯模型

假设我们已经有部分数据，并且能从数据中得到先验概率，那么如何得到后验概率P(Yk|X)呢？下面我们通过构建朴素贝叶斯分类模型来解决后验概率问题，假设分类模型数据有m个样本，每个样本有n个特征，特征输出有K个类别，定义为C1,C2,…,Ck

从样本中学到朴素贝叶斯的先验分布概率：P(Y=Ck)(k=1,2,…,K)

得到条件概率分布：P(X|Y=Ck)=P(X1=x(1),X2=x(2),...,Xn=x(n)|Y=Ck)

结合贝叶斯公式得X和Y的联合分布P(X,Y=Ck)

P(X,Y=Ck)=P(Y=Ck)P(X|Y=Ck)                             (1)

=P(Y=Ck)P(X1=x(1),X2=x(2),...,Xn=x(n)|Y=Ck)                      (2)

上式中P(Y=Ck)可以通过极大似然法求出，得到的P(Y=Ck)就是类别Ck在训练集里面出现的频数。但是P(X1=x(1),X2=x(2),...,Xn=x(n)|Y=Ck)很难求出，因此朴素贝叶斯模型做一个大胆的假设，即X的n个维度之间相互独立，这样就可以得出

P(X1=x(1),X2=x(2),...,Xn=x(n)|Y=Ck)

=P(X1=x(1)|Y=Ck)P(X2=x(2)|Y=Ck),...,P(Xn=x(n)|Y=Ck)

这样我们便得到X和Y的联合分布，最后的问题是给定测试集

 

3.5朴素贝叶斯推断

 

3.6朴素贝叶斯参数估计

3.7 算法流程

假设训练集有m个样本n个维度，训练样本有K个特征输出类别，分别为C1,C2,…,CK，每个特征输出类别的样本个数为m1,m2,…,mK。第K个类别中，如果是离散特征，则特征Xj各个类别取值为mjl，其中l的取值为1,2,…,Sj，Sj为特征j不同的取值数

从上面计算可以看出，朴素贝叶斯没有复杂的求导和矩阵运算，因此效率很高。但朴素贝叶斯假设数据特征之间相互独立，如果数据特征之间关联性比较强的话，我们尽量不要使用朴素贝叶斯算法，考虑其他分类方法比较好。

 

3.8应用

1. 描述：利用sklearn自带的iris数据集进行训练，选取70%的数据当作训练集，30%的数据当作测试集。因iris数据集为连续值，所以采用GaussianNB模型，训练后模型得分为0.933333333333

from sklearn.naive_bayes import GaussianNB
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split

#load data
iris=load_iris()
X=iris.data
y=iris.target
X_train,X_test,y_train,y_test=train_test_split(X,y,test_size=0.3,random_state=1)

mnb=GaussianNB()
mnb.fit(X_train,y_train)

print(mnb.predict(X_test))
# [0 1 1 0 2 2 2 0 0 2 1 0 2 1 1 0 1 1 0 0 1 1 2 0 2 1 0 0 1 2 1 2 1 2 2 0 1
#  0 1 2 2 0 1 2 1]
print(y_test)
# [0 1 1 0 2 1 2 0 0 2 1 0 2 1 1 0 1 1 0 0 1 1 1 0 2 1 0 0 1 2 1 2 1 2 2 0 1
#  0 1 2 2 0 2 2 1]
print(mnb.score(X_test,y_test))
# 0.933333333333

 

1. 支持向量机（Support Vector Machine）

线性可分（Linear Separable）

线

 

问题描述

支持向量：擦到样本点的线

间隔（Margin）：支持向量间的距离

2号线是使间隔最大的一条线，且在上下两个平行线的中间

最优分类直线（基于二维空间）：

• 该直线分开了两类
• 有最大化间隔
• 处于间隔的中间，到所有支持向量的距离相等

在多维中，直线变为超平面，适用。

优化问题

假设训练样本集是线性可分的，SVM找出最大化间隔的超平面

1也可为任意一个整数。应为还在同一个平面

线性不可分的情况

支持向量机引入松弛变量，参数C增加对最终结果有什么影响？

参数C决定支持向量机的损失函数支持向量机引入松弛变量我认为是因为在实际情况中，训练样本存在这样的情况：某些样本点无法被正确地划分，但是我们没必要硬是将其全部划分，模型应该有一点的容忍度。对于参数C我同意同学“mooc_userwu”的看法，即：参数C表示对误差的容忍度，C越大表示越不能容忍误差，当C非常大时则容易过拟合，从而降低模型的泛化能力，C非常小则容易欠拟合从而无法在训练集上取得比较好的结果，C过大过小都会降低模型泛化能力。

不存在ω和b满足上面N个限制条件

此刻需要适当的放松限制条件。

基本思路：对于每一个训练样本及标签（xi，yi），设置松弛变量δi，同时加入新的限制，δi，不会无限变大

C是人为设定的参数，被称为算法的超参数。

在应用过程中，我们不断变化c1的值来测试算法的识别率，最终选取超参数c。（SVM超参数很少，但是人工神经网络和卷积神经网络超参数就很多）

参数C可以平衡松弛变量带来的影响。比如说当C取得很大的时候，要想让w最小，松弛变量就应该足够的小才行假如不是线性的呢？

1. 对方程组进行求解，最后检查下得到的解是否确实为一个最小值

4.7规则化不可分的参数

在原对偶式子中加入离群点权重C，问题转化为maxαW(α)

4.8求解W(α)的最优值

利用SMO优化算法求解 W(α)的最优值，

1. 选择两个要改变的α值αi，αj ​，
2. 保持除了αi，αj之外的所有参数固定。
3. 相对于这两个参数使 ω取最优，且同时满足所有约束条件，最后确定选取的这两个αi，αj的值
4. 一直重复步骤1) ~ 3)，直至所有参数α求解完成。

4.9实现

from sklearn import svm
import numpy as np
import matplotlib.pyplot as plt

np.random.seed(0)
x=np.r_[np.random.randn(20,2)-[2,2],np.random.randn(20,2)+[2,2]]#正态分布产生数字20行2列
y=[0]*20+[1]*20#20个class0,20个class1
clf=svm.SVC(kernel='linear')#使用线性核
clf.fit(x,y)
w=clf.coef_[0]#获取w
a=-w[0]/w[1]#斜率

#画图
xx=np.linspace(-5,5)
yy=a*xx-(clf.intercept_[0])/w[1]
b=clf.support_vectors_[0]
yy_down=a*xx+(b[1]-a*b[0])
b=clf.support_vectors_[-1]
yy_up=a*xx+(b[1]-a*b[0])
plt.figure(figsize=(8,4))
plt.plot(xx,yy)
plt.plot(xx,yy_down)
plt.plot(xx,yy_up)
plt.scatter(clf.support_vectors_[:,0],clf.support_vectors_[:,1],s=80)
plt.scatter(x[:,0],x[:,1],c=y,cmap=plt.cm.Paired)
plt.axis('tight')
plt.show()

1. EM

9.1 原理

要解决的问题 　

我们经常会从样本观察数据中，找出样本的模型参数。 最常用的方法就是极大化模型分布的对数似然函数。  　　　　但是在一些情况下，我们得到的观察数据有未观察到的隐含数据，此时我们未知的有隐含数据和模型参数， EM算法解决这个的思路是使用启发式的迭代方法，E步估计隐含变量，M步估计其他参数，接着基于观察数据和猜测的隐含数据一起来极大化对数似然,以此类推，不断的迭代下去，直到模型分布参数基本无变化，算法收敛，找到合适的模型参数。

用于估计含有隐变量的概率模型参数的极大似然估计，或者极大后验概率估计。当概率模型既含有观测值，又含有隐变量或潜在变量时，就可以使用EM算法来求解概率模型的参数。当概率模型只含有观测值时，直接使用极大似然估计法，或者贝叶斯估计法估计模型参数就可以了。

基本思想是：首先根据己经给出的观测数据，估计出模型参数的值；然后再依据上一步估计出的参数值估计缺失数据的值，再根据估计出的缺失数据加上之前己经观测到的数据重新再对参数值进行估计，然后反复迭代，直至最后收敛，迭代结束。

一个最直观了解EM算法思路的是：k-means算法是EM算法思想的体现，E步骤为聚类过程，M步骤为更新类簇中心。GMM（高斯混合模型）也是EM算法的一个应用，

 

ps：图片太多，转载不了，有需要的请网盘自取链接：https://pan.baidu.com/s/1KL5vuCqNM8rCH3MqX-mzTQ 
提取码：00n0