动态规划-----爬楼梯

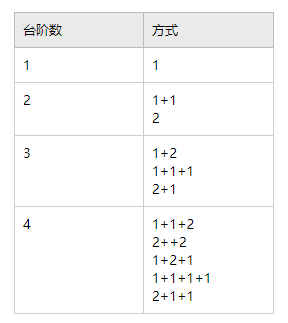
题目描述：共有n个台阶，每次只能走1，2个，完成走完n个台阶共有多少中方式

 解析：第n个台阶走几步取决于 走到n-1和n-2的方式 ，因为走完n-1还剩1阶台阶，走完n-2还剩2个台阶，所以都只需要再走1步即可，所以是 count(n) = count(n-1)+count(n-2);

 

private static int stepMethods(int n) {
        if (n == 1) {
            return 1;
        } else if (n == 2) {
            return 2;
        } else {
            return stepMethods(n - 1) + stepMethods(n - 2);
        }
    }

拓展：若每次可以走1，2，...，m个台阶，则count(n) = count(n-1)+count(n-2)+...+count(m);