并查集总结_并查集怎么去记录这个数的根有多少个孩子-优快云博客

本文链接：https://blog.youkuaiyun.com/ZhuRanCheng/article/details/118945763

本文详细介绍了并查集的基本概念、实现方法，包括初始化、查询、合并操作，以及优化策略如路径压缩和按秩合并。还涵盖了带权并查集和种类并查集的应用，通过实例分析了银河英雄传说、团伙和食物链问题。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

并查集

一、并查集

1. 定义

并查集 (union - findset) 是一种表示不相交集合的数据结构，常用于处理不相交集合的合并与查询问题；

每个集合通过代表来区分，代表是集合中的某个成员，能够起到唯一标识该集合的作用；

选择哪一个元素作为代表是无关紧要的，主要为在进行查找操作时，得到的答案一致；

则并查集主要用于动态维护许多具有传递性的关系；

2. 实现方法

并查集的实现方法为使用有根树来表示集合，树中的每个节点都表示集合的一个元素，每棵树的根节点作为该集合的代表；

使用 $f a t h er$ 数组表示 $i$ 节点的父亲节点，则可通过 $f a t h er$ 数组来表示出整棵树，及整个并查集，具体操作如下；

二、基本操作

1. 初始化

思路

共有 $n$ 个元素，进行初始化，初始化时节点的父节点即为本身，即自己代表自己；

代码

void FirstSet(int n) {
	for (int i = 1; i <= n; i++) {
		father[i] = i;
	}
	return;
}

2. 查询

思路

查询操作为递归查询，查询某个结点在哪一个集合中时，需沿着其父结点，递归向上；

由于所属集合代表指向的仍然是其本身，所以 father[x] == x 作为递归查询出口；

代码

int FindSet(int x) {
	if (father[x] == x) return x;
	return FindSet(father[x]); 
}

3. 合并

思路

在进行集合合并时，只需将两个集合的代表进行连接即可，即一个代表作为另一个代表的父节点；

则剩下的节点根节点均会在遍历时根据其父节点遍历到新的根节点；

代码

void UnionSet(int x, int y) {
	father[FindSet(x)] = FindSet(y);
	return;
}

四、优化

1. 路径压缩

说明

对于一个集合中的结点，由于只需知道它的根结点是谁，不必知道各结点之间的关系，又由于在查询过程中，离根节点越近查询时间越快，所以希望每个元素到根结点的路径尽可能短，即可极大提高了查询效率;

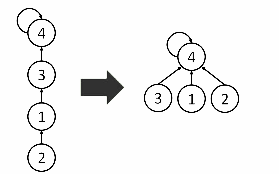
路径压缩优化即为在操作时，把沿途的每个父节点都设为根节点即可，下一次在查询时，可节约许多时间；

代码

int FindSet(int x) {
	if (father[x] == x) return x;
	return father[x] = FindSet(father[x]);
}

2. 按秩合并

说明

由于路径压缩只在查询时进行，每一次查询也只压缩一条路径，所以在并查集的最终结构也可能比较复杂时，查询效率仍不高；

则可使用按秩合并即将深度低的集合往深度大的集合上合并；

可使用 $r ank 1$ 数组记录根节点对应的树的深度，若不为根节点，其 $r ank 1$ 值相当于以其作为根节点的子树的深度；

初始化时，将所有 $r ank 1$ (秩) 设为 1 ;

合并时比较两个根的结点，把 $r ank 1$ 较小者往较大者上合并即可；

代码

void FirstSet(int n) {
	for (int i = 1; i <= n; i++) {
		father[i] = i, rank1[i] = 1;
	}
	return;
}
void UnionSet(int x, int y) {
	int a = FindSet(x), b = FindSet(y);
    if (a == b) return;
    if (rank1[a] <= rank1[b]) father[a] = b;
    else father[b] = a;
    if (rank1[a] == rank1[b]) rank1[b]++;
    return;
}

五、带权并查集

1. 说明

并查集实际为森林，则可以在树中每条边上记录一个权值，用于维护该节点与其祖先节点的关系，则每次在路径压缩时可同时更新维护的权值，可利用路径压缩过程来统计某个节点到树根上的一些信息，这即为带权并查集；

2. 例题

[NOI2002] 银河英雄传说

题意

有两种指令，一种为将 $i$ 所在集合接到 $j$ 的末尾，另一种即为查询 $i$ 与 $j$ 之间相隔元素的数量并输出；

思路

由于需要合并以及查询元素之间的元素相隔数量，所以可以使用带权并查集；

则可维护 $d i s$ 数组表示 $i$ 到其根节点的距离；

查询答案

即先判断查询节点 $x$ 与 $y$ 是否在同一集合中，若不在，输出 -1 ;

则 $x$ 与 $y$ 之间的元素数量即为 $x$ 到根节点的距离减去 $y$ 到根节点的距离再 - 1，即 $d i s [x] - d i s [y] - 1$ ；

但由于不知道 $d i s [x]$ 与 $d i s [y]$ 的大小关系，所以加绝对值；

又由于当 x == y 时，最终答案应为 0 ，所以还要判断；

if (findset(x) != findset(y)) printf("-1\n");
else if (x == y) printf("0\n");
else printf("%d\n", abs(dis[x] - dis[y]) - 1);

查询祖先

查询祖先时，沿着祖先遍历到根节点时更新 $d i s$ 数组；

由于其根节点在合并时接在了另一个集合后，则当前节点的原 $d i s$ 值加上其父节点的 $d i s$ 值，即为新的 $d i s$ 值；

int findset(int x) {
	if (father[x] == x) return x;
	int y = findset(father[x]);
	dis[x] += dis[father[x]];
	return father[x] = y;
}

合并

由于 $x$ 接在了 $y$ 下面，所以 $d i s [y]$ 应该加上 $x$ 所在集合的元素个数，所以还需数组 $s i ze$ 维护 $i$ 的根节点所在集合的元素个数；

则由于 $x$ 接在了 $y$ 下，所以 $b$ 的根节点所在集合的元素个数应加上 $a$ 的根节点所在集合的元素个数；

void unionset(int x, int y) {
	int a = findset(x), b = findset(y);
	if (a == b) return;
	father[a] = b;
	dis[a] = size[b];
	size[b] += size[a];
	return;
}

初始化

将每个节点父节点设为自己，元素个数设为 1 ， $d i s$ 数组设为 0 ；

void firstset(int n) {
	for (int i = 1; i <= n; i++) {
		father[i] = i, size[i] = 1, dis[i] = 0;
	}
	return;
}

代码

#include <cstdio>
#include <algorithm>
#define MAXN 30005
using namespace std;
int n, father[MAXN], dis[MAXN], size[MAXN];
void firstset(int n) {
	for (int i = 1; i <= n; i++) {
		father[i] = i, size[i] = 1, dis[i] = 0;
	}
	return;
}
int findset(int x) {
	if (father[x] == x) return x;
	int y = findset(father[x]);
	dis[x] += dis[father[x]];
	return father[x] = y;
}
void unionset(int x, int y) {
	int a = findset(x), b = findset(y);
	if (a == b) return;
	father[a] = b;
	dis[a] = size[b];
	size[b] += size[a];
	return;
}
int main() {
	firstset(30000);
	scanf("%d", &n);
	for (int i = 1; i <= n; i++) {
		char c;
		int x, y;
		scanf("\n%c %d %d", &c, &x, &y);
		if (c == 'M') {
			unionset(x, y);
		} else {
			if (findset(x) != findset(y)) printf("-1\n");
			else if (x == y) printf("0\n");
			else printf("%d\n", abs(dis[x] - dis[y]) - 1);
		}
	}
	return 0;
}

六、种类并查集

1. 说明

一般的并查集，维护的是具有连通性、传递性的关系，但有时需要维护两种相矛盾的关系，则可再开几个维护矛盾关系的并查集；

则可多开几个维护不同关系的并查集元素；

合并时，一定将最后合并完后的根结点设在实点上，否则无法遍历；

2. 例题

[BOI2003]团伙

题目描述

在某城市里住着n个人，任何两个认识的人不是朋友就是敌人，而且满足：

朋友的朋友是的朋友；
敌人的敌人是的朋友；

所有是朋友的人组成一个团伙。告诉你关于这n个人的m条信息，即某两个人是朋友，或者某两个人是敌人，请你编写一个程序，计算出这个城市最多可能有多少个团伙？

思路

因为题目中有两种关系，敌人与朋友，利用种类并查集，将空间开到原数组的两倍；

$\sim n$ 实点表示 $i, j$ 的朋友关系，虚点表示 $i, j$ 的敌人关系;

初始化

初始化的时候，将实点与虚点均设为 $f a t h er [i] = i$ ；

void firstset(int n) {
	for (int i = 1; i <= n * 2; i++) {
		father[i] = i;
	}
	return;
}

合并

合并时，朋友合并 $x, y$ 即可，敌人合并先合并 $y + n, x$ 表示 $x$ 为 $y$ 的敌人，再合并 $x + n, y$ 表示 $x$ 为 $y$ 的敌人，注意，一定要将虚点的并查集接入的实点上，才可合并完后遍历不同祖先的个数；

void unionset(int x, int y) {
	father[findset(x)] = findset(y);
	return;
}
if (f == 'F') {
    unionset(x, y);
} else {
    unionset(x + n, y);
    unionset(y + n, x);
}

计算答案

即遍历每个实点，判断为集合根节点的节点的个数即可；

for (int i = 1; i <= n; i++) {
    if (findset(i) == i) {
        ans++;
    }
}

代码

#include <cstdio>
#include <algorithm>
#define MAXN 1005
using namespace std;
int n, m, father[MAXN * 2], ans;
void firstset(int n) {
	for (int i = 1; i <= n * 2; i++) {
		father[i] = i;
	}
	return;
}
int findset(int x) {
	if (father[x] == x) return x;
	return father[x] = findset(father[x]);
}
void unionset(int x, int y) {
	father[findset(x)] = findset(y);
	return;
}
int main() {
	scanf("%d %d", &n, &m);
	firstset(n);
	for (int i = 1; i <= m; i++) {
		int x, y;
		char f;
		scanf("\n%c %d %d", &f, &x, &y);
		if (f == 'F') {
			unionset(x, y);
		} else {
			unionset(x + n, y);
			unionset(y + n, x);
		}
	}
	for (int i = 1; i <= n; i++) {
		if (findset(i) == i) {
			ans++;
		}
	}
	printf("%d", ans);
	return 0;
}

[NOI2001] 食物链

题目

三类动物 A,B,C，这三类动物的食物链构成了有趣的环形。A 吃 B，B 吃 C，C 吃 A。

现有 N 个动物，以 1 － N 编号。每个动物都是 A,B,C 中的一种，但是我们并不知道它到底是哪一种。

有人用两种说法对这 N 个动物所构成的食物链关系进行描述：

第一种说法是 1 X Y，表示 X 和 Y 是同类。
第二种说法是2 X Y，表示 X 吃 Y 。

此人对 N 个动物，用上述两种说法，一句接一句地说出 K 句话，这 K 句话有的是真的，有的是假的。当一句话满足下列三条之一时，这句话就是假话，否则就是真话。

当前的话与前面的某些真的话冲突，就是假话
当前的话中 X 或 Y 比 N 大，就是假话
当前的话表示 X 吃 X，就是假话

你的任务是根据给定的 N 和 K 句话，输出假话的总数。

分析

由于题目中有 3 类动物，又由于三类动物的关系为相矛盾的，所以想到种类并查集；

将并查集扩展 3 倍，分别表示与同类，捕食的与天敌；

则可将并查集开为如下，

$\sim n$	$\sim n * 2$	$\sim n * 3$
$x_{self}$	$x_{eat}$	$x_{enemy}$
同类	捕食的	天敌

则对于判断 $x$ 与 $y$ 同类的操作，如下，

若 $x_{self}$ 与 $y_{eat}$ 在同一集合，则说明 $y$ 吃 $x$ ，则说法错误；
若 $x_{eat}$ 与 $y_{self}$ 在同一集合，则说明 $x$ 吃 $y$ ，则说法错误；
否则，则说法正确， $x$ 与 $y$ 同类，则修改并查集，
1. 将 $x_{self}$ 与 $y_{self}$ 放入同一集合；
2. 将 $x_{eat}$ 与 $y_{eat}$ 放入同一集合；
3. 将 $x_{enemy}$ 与 $y_{enemy}$ 放入同一集合；

对于判断 $x$ 吃 $y$ 的操作，如下，

若 $x_{self}$ 与 $y_{self}$ 在同一集合，则说明 $x$ 与 $y$ 同类，说法错误；
若 $x_{enemy}$ 与 $y_{self}$ 在同一集合，则说明 $y$ 吃 $x$ ，则说法错误；
若 $x_{self}$ 与 $y_{eat}$ 在同一集合，则说明 $y$ 吃 $x$ ，则说法错误；
否则，则说法正确， $x$ 吃 $y$ ，则修改并查集，
1. 将 $x_{self}$ 与 $y_{enemy}$ 放入同一集合；
2. 将 $x_{eat}$ 与 $y_{self}$ 放入同一集合；
3. 将 $x_{enemy}$ 与 $y_{eat}$ 放入同一集合；

则通过上述方法维护并查集并判断答案正误即可；

代码

#include <cstdio>
#include <algorithm>
#define MAXN 50005
using namespace std;
int n, k, ans, father[MAXN * 3];
void firstset(int n) {
	for (int i = 1; i <= n * 3; i++) {
		father[i] = i;
	}
	return;
}
int findset(int x) {
	if (father[x] == x) return x;
	return father[x] = findset(father[x]);
}
void unionset(int x, int y) {
	father[findset(x)] = findset(y);
	return;
}
int main() {
	scanf("%d %d", &n, &k);
	firstset(n);
	for (int i = 1; i <= k; i++) {
		int d, x, y;
		scanf("%d %d %d", &d, &x, &y);
		if (x > n || y > n) {
			ans++;
			continue;
		}
		if (d == 1) {
			if ((findset(x + n) == findset(y)) || (findset(x) == findset(y + n))) {
				ans++;
			} else {
				unionset(x, y);
				unionset(x + n, y + n);
				unionset(x + 2 * n, y + 2 * n);
			}
		} else {
			if (((findset(x) == findset(y)) || (findset(x + 2 * n) == findset(y)) || (findset(x) == findset(y + n)))) {
				ans++;
			} else {
				unionset(x, y + 2 * n);
				unionset(x + n, y);
				unionset(x + 2 * n, y + n);
			}
		}
	}
	printf("%d", ans);
	return 0;
}