【力扣算法】37-解数独

题目

编写一个程序，通过已填充的空格来解决数独问题。

一个数独的解法需遵循如下规则：

1. 数字 1-9 在每一行只能出现一次。
2. 数字 1-9 在每一列只能出现一次。
3. 数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。

空白格用 '.' 表示。

一个数独。

答案被标成红色。

Note:

• 给定的数独序列只包含数字 1-9 和字符 '.' 。
• 你可以假设给定的数独只有唯一解。
• 给定数独永远是 9x9 形式的。

题解

方法 0：蛮力法

首先的想法是通过蛮力法来生成所有可能用1 到 9填充空白格的解， 并且检查合法从而保留解。这意味着共有 $9^{81}$ 个操作需要进行。 其中 99 是可行的数字个数，81 是需要填充的格子数目。 因此我们必须考虑进一步优化。

---

方法 1：回溯法

使用的概念

了解两个编程概念会对接下来的分析有帮助。

第一个叫做 约束编程。

基本的意思是在放置每个数字时都设置约束。在数独上放置一个数字后立即 排除当前 行， 列 和 子方块 对该数字的使用。这会传播 约束条件 并有利于减少需要考虑组合的个数。

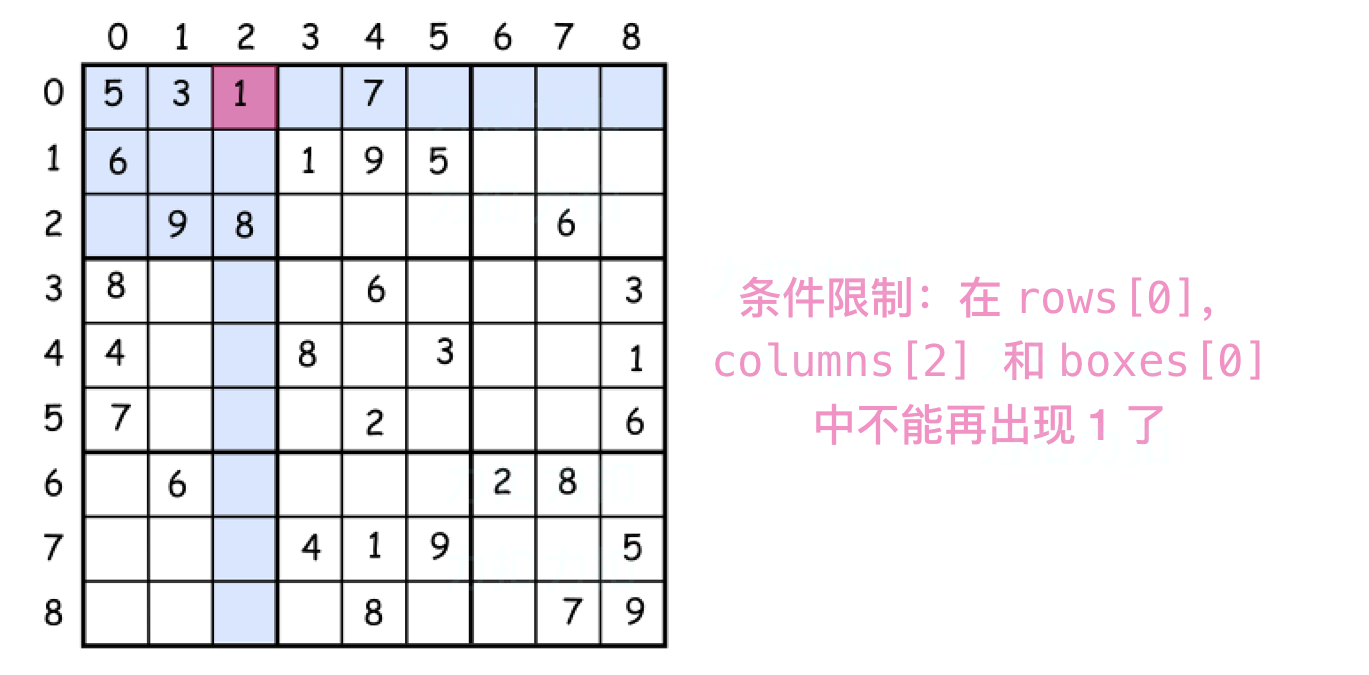
第二个叫做 回溯。

让我们想象一下已经成功放置了几个数字 在数独上。 但是该组合不是最优的并且不能继续放置数字了。该怎么办？ 回溯。 意思是回退，来改变之前放置的数字并且继续尝试。如果还是不行，再次 回溯。

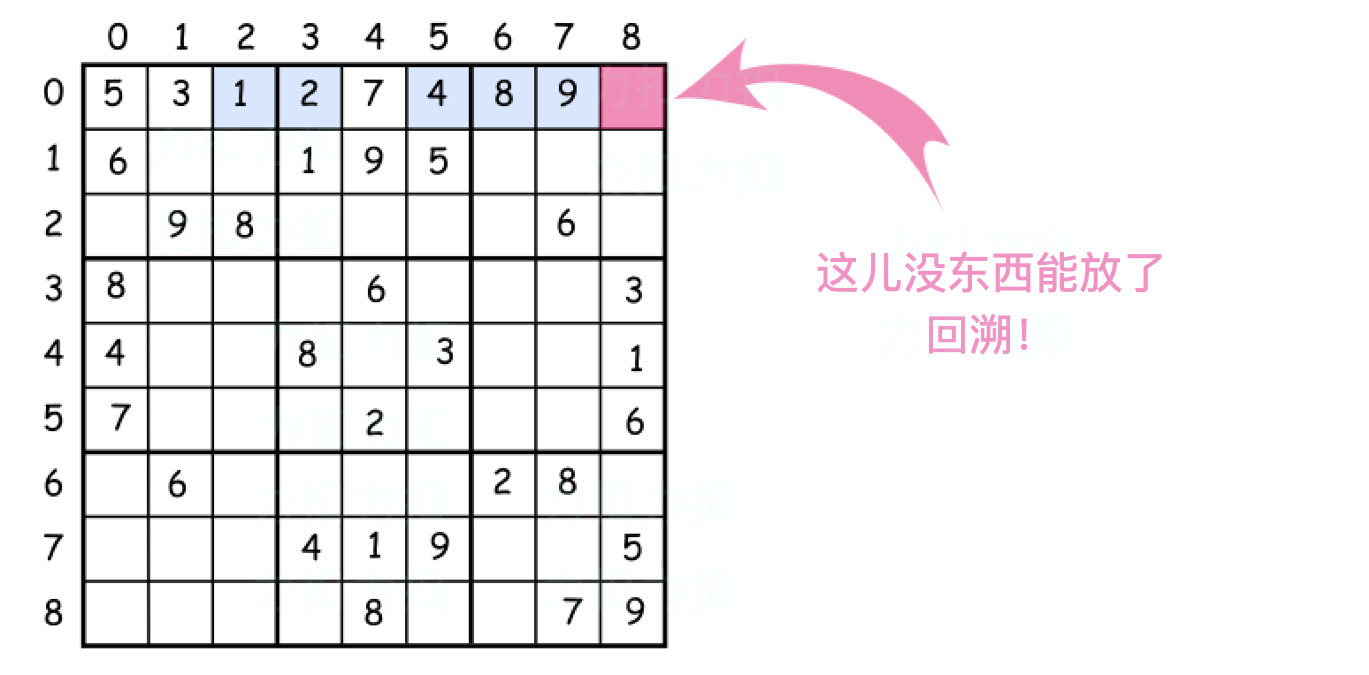
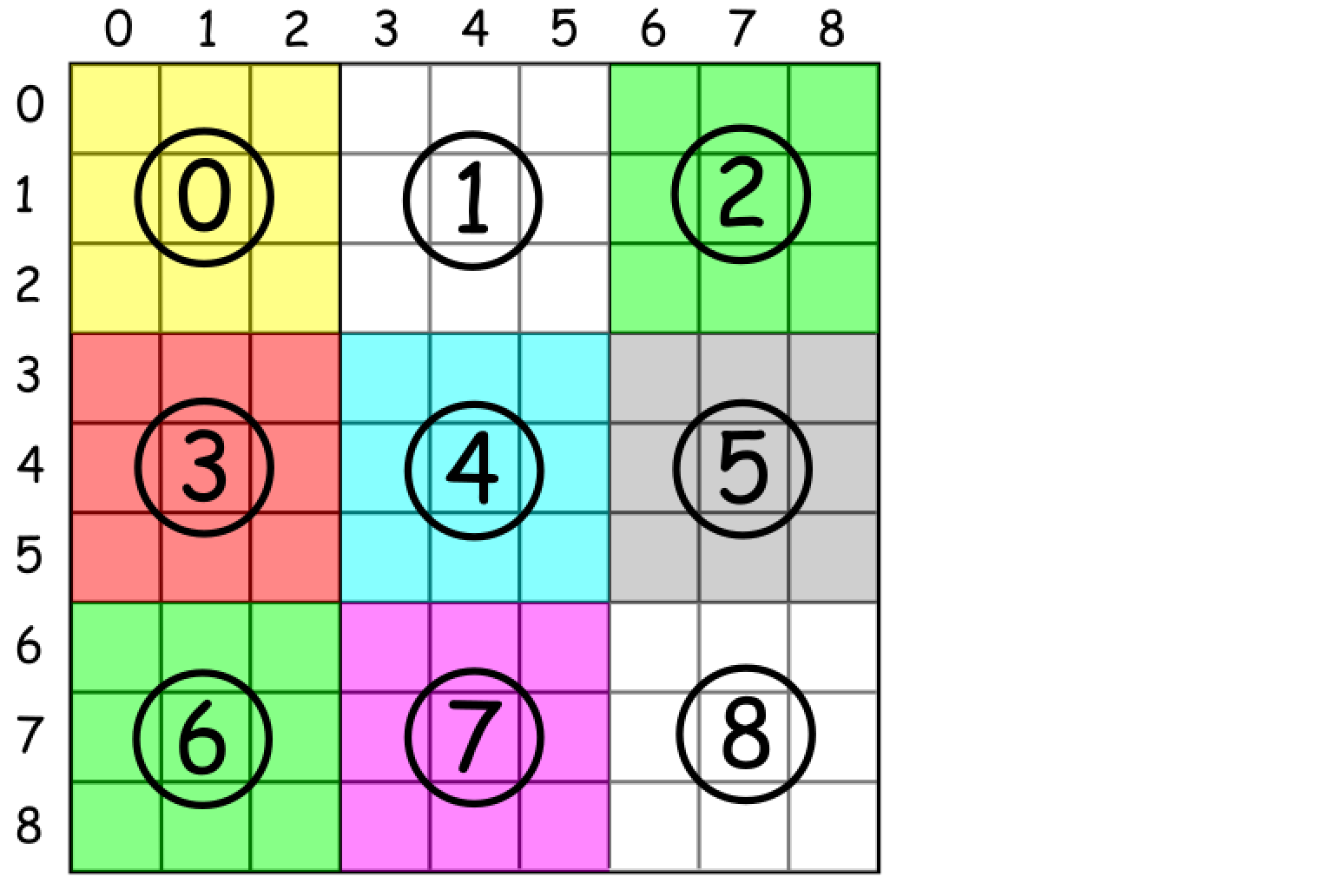
如何枚举子方块

一种枚举子方块的提示是：

使用 方块索引= (行 / 3) * 3 + 列 / 3 其中 / 表示整数除法。

算法

现在准备好写回溯函数了 backtrack(row = 0, col = 0)。

• 从最左上角的方格开始 row = 0, col = 0。直到到达一个空方格。
• 从1 到 9 迭代循环数组，尝试放置数字 d 进入 (row, col) 的格子。
  • 如果数字 d 还没有出现在当前行，列和子方块中：
    • 将 d 放入 (row, col) 格子中。
    • 记录下 d 已经出现在当前行，列和子方块中。
    • 如果这是最后一个格子row == 8, col == 8：
      • 意味着已经找出了数独的解。
    • 否则
      • 放置接下来的数字。
    • 如果数独的解还没找到： 将最后的数从 (row, col) 移除。

代码

• Java

class Solution {
  // box size
  int n = 3;
  // row size
  int N = n * n;

  int [][] rows = new int[N][N + 1];
  int [][] columns = new int[N][N + 1];
  int [][] boxes = new int[N][N + 1];

  char[][] board;

  boolean sudokuSolved = false;

  public boolean couldPlace(int d, int row, int col) {
    /*
    Check if one could place a number d in (row, col) cell
    */
    int idx = (row / n ) * n + col / n;
    return rows[row][d] + columns[col][d] + boxes[idx][d] == 0;
  }

  public void placeNumber(int d, int row, int col) {
    /*
    Place a number d in (row, col) cell
    */
    int idx = (row / n ) * n + col / n;

    rows[row][d]++;
    columns[col][d]++;
    boxes[idx][d]++;
    board[row][col] = (char)(d + '0');
  }

  public void removeNumber(int d, int row, int col) {
    /*
    Remove a number which didn't lead to a solution
    */
    int idx = (row / n ) * n + col / n;
    rows[row][d]--;
    columns[col][d]--;
    boxes[idx][d]--;
    board[row][col] = '.';
  }

  public void placeNextNumbers(int row, int col) {
    /*
    Call backtrack function in recursion
    to continue to place numbers
    till the moment we have a solution
    */
    // if we're in the last cell
    // that means we have the solution
    if ((col == N - 1) && (row == N - 1)) {
      sudokuSolved = true;
    }
    // if not yet
    else {
      // if we're in the end of the row
      // go to the next row
      if (col == N - 1) backtrack(row + 1, 0);
        // go to the next column
      else backtrack(row, col + 1);
    }
  }

  public void backtrack(int row, int col) {
    /*
    Backtracking
    */
    // if the cell is empty
    if (board[row][col] == '.') {
      // iterate over all numbers from 1 to 9
      for (int d = 1; d < 10; d++) {
        if (couldPlace(d, row, col)) {
          placeNumber(d, row, col);
          placeNextNumbers(row, col);
          // if sudoku is solved, there is no need to backtrack
          // since the single unique solution is promised
          if (!sudokuSolved) removeNumber(d, row, col);
        }
      }
    }
    else placeNextNumbers(row, col);
  }

  public void solveSudoku(char[][] board) {
    this.board = board;

    // init rows, columns and boxes
    for (int i = 0; i < N; i++) {
      for (int j = 0; j < N; j++) {
        char num = board[i][j];
        if (num != '.') {
          int d = Character.getNumericValue(num);
          placeNumber(d, i, j);
        }
      }
    }
    backtrack(0, 0);
  }
}

复杂性分析

• 这里的时间复杂性是常数由于数独的大小是固定的，因此没有 N 变量来衡量。 但是我们可以计算需要操作的次数：$(9!{)}^9$。 我们考虑一行，即不多于 99 个格子需要填。 第一个格子的数字不会多于 99 种情况， 两个格子不会多于 $9\times 8$ 种情况， 三个格子不会多于 $9\times 8\times 7$ 种情况等等。 总之一行可能的情况不会多于 9! 种可能， 所有行不会多于 $(9!{)}^9$ 种情况。比较一下：
  • 9⁸¹ = 196627050475552913618075908526912116283103450944214766927315415537966391196809 为蛮力法，
  • 而 $(9!{)}^9$ = 109110688415571316480344899355894085582848000000000 为回溯法， 即数字的操作次数减少了 $10^{27}$ 倍！
• 空间复杂性：数独大小固定，空间用来存储数独，行，列和子方块的结构，每个有 81 个元素。

感想

自己的思路本来是想用可以直接确定的情况来给回溯法剪枝的，但是自己的剪枝写的还是不咋地，只能剪一次。按道理是每一次attempt都要重新剪一下的，但是自己嫌麻烦就没写了。所以最后实现的总思路是，先把能直接确定的格子填满，然后再调用回溯法去试。最后得到的效率不怎么样。

执行用时 : 15 ms, 在Sudoku Solver的Java提交中击败了39.47% 的用户

内存消耗 : 35.4 MB, 在Sudoku Solver的Java提交中击败了71.06% 的用户

class Solution {
    boolean[][] row = new boolean[9][9];
    boolean[][] col = new boolean[9][9];
    boolean[][] box = new boolean[9][9];
    HashSet<Integer>[][] possible = new HashSet[9][9];
    int count = 0;

    public void solveSudoku(char[][] board) {

        for (int i = 0; i < 9; i++) {
            for (int j = 0; j < 9; j++) {
                possible[i][j] = new HashSet<Integer>();
                Collections.addAll(possible[i][j], 0, 1, 2, 3, 4, 5, 6, 7, 8);
            }
        }
        for (int i = 0; i < 9; i++) {
            for (int j = 0; j < 9; j++) {
                if (board[i][j] == '.') continue;
                int num = board[i][j] - '1';

                row[i][num] = col[j][num] = box[i / 3 * 3 + j / 3][num] = true;

                for (int k = 0; k < 9; k++) {
                    possible[i][k].remove(num);
                    possible[k][j].remove(num);
                }
                for (int k1 = i - i % 3; k1 < i - i % 3 + 3; k1++) {
                    for (int k2 = j - j % 3; k2 < j - j % 3 + 3; k2++) {
                        possible[k1][k2].remove(num);
                    }
                }
                count++;
                possible[i][j].clear();
            }
        }
        solveSudokuDefinite(board);
    }

    private boolean solveSudokuDefinite(char[][] board) {
        while (count < 81) {
            int check = count;
            for (int i = 0; i < 9; i++) {
                for (int j = 0; j < 9; j++) {
                    if (possible[i][j].size() == 1 && board[i][j] == '.') {
                        int num = -1;
                        for (int integ : possible[i][j]) num = integ;

                        row[i][num] = col[j][num] = box[i / 3 * 3 + j / 3][num] = true;

                        board[i][j] = (char) (num + '1');
                        for (int k = 0; k < 9; k++) {
                            possible[i][k].remove(num);
                            possible[k][j].remove(num);
                        }
                        for (int k1 = i - i % 3; k1 < i - i % 3 + 3; k1++) {
                            for (int k2 = j - j % 3; k2 < j - j % 3 + 3; k2++) {
                                possible[k1][k2].remove(num);
                            }
                        }
                        count++;
                        possible[i][j].clear();
                    }
                }
            }

            if (check == count) {
                solveSudokuAttempt(board);
                break;
            }

        }
        return true;
    }

    private boolean solveSudokuAttempt(char[][] board) {
        if(count==81) return true;
        int x=0;
        int y=0;
        loop:
        for (x = 0; x < 9; x++) {
            for (y = 0; y < 9; y++) {
                if (board[x][y] == '.') break loop;
            }
        }
        if(x==9||y==9) return false;
        for (int integ : possible[x][y]) {
            int num = integ;
            boolean rowbackup = row[x][num];
            boolean colbackup = col[y][num];
            boolean boxbackup = box[x / 3 * 3 + y / 3][num];
            if(rowbackup|colbackup|boxbackup) continue;
            board[x][y] = (char) (num + '1');
            count++;
            row[x][num] = col[y][num] = box[x / 3 * 3 + y / 3][num] = true;

            if (solveSudokuAttempt(board)) return true;
            else {
                count--;
                board[x][y] = '.';
                row[x][num] = rowbackup;
                col[y][num] = colbackup;
                box[x / 3 * 3 + y / 3][num] = boxbackup;
            }
        }
        return false;
    }
}