DETR-二分图匹配 & 匈牙利算法

原创 已于 2022-10-24 14:48:31 修改 · 4.6k 阅读 · 22 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#1024程序员节 #目标检测 #算法 #计算机视觉

于 2022-10-24 10:50:49 首次发布
DETR通过将目标检测转化为二分图匹配问题，利用匈牙利算法找到最佳框匹配，降低了复杂度。线性_sum_assignment函数用于计算最小成本匹配，其中cost_matrix包含了分类和定位loss。这种方法避免了NMS后处理，直接得到一对一匹配，简化了目标检测模型的训练和部署。

文章目录

前言

DETR提出了基于Query的端到端目标检测算法，把目标检测看成了一个集合预测问题，大大简化了模型的训练和部署。(详见DETR的学习与分析)其中，DETR模型实现的创新点之一就是基于集合的目标函数，那么具体来说这个目标函数是如何设计的呢？二分图匹配、匈牙利算法、一对一匹配都是什么意思？

1. 二分图匹配问题

DETR模型最后的输出是一个固定的集合，即不论输入图片中包含多少目标，最后都会输出N个框（一般N远大于图片中的目标数目）。问题来了，一张图片中Ground Truth（真值）的bounding box（边界框）可能只有几个，那么如何匹配预测框与Ground Truth框呢？
作者将这个问题转化为了二分图匹配的问题。
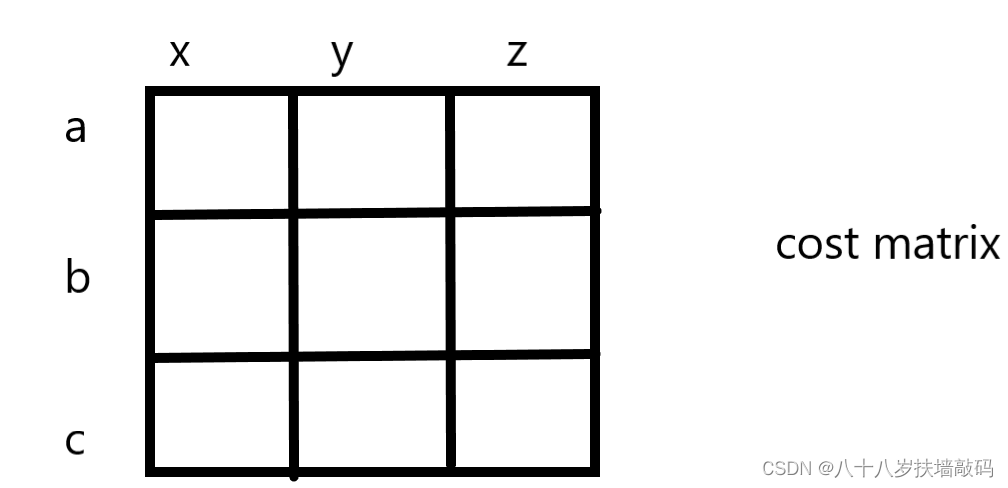
例子：有abc三个工人，去干xyz三种工作，由于每个工人各有所长，所以完成每种工作的开销不同，如何分配工人做这三种工作，可以使开销最小？
最优二分图匹配即最后可以找到一个唯一的解，能够给每个人对应分配最擅长的工作，使得开销最小。
在这里插入图片描述

2.匈牙利算法

对于上述问题，可以直接暴力穷举，遍历所有可能，找出其中最小开支，但是算法的复杂度会很高。而匈牙利算法则是可以用较低的复杂度解决

最低0.47元/天 解锁文章
东方采菊
关注
【人工智能专栏】二分图匹配与匈牙利算法，出现在 **DETR** 的目标检测匹配上
热情、奔放、快乐编程！
07-31 223
二分图匹配与匈牙利算法，出现在的目标检测匹配上。二分图又称作二部图，是图论中的一种特殊模型。设GVE是一个无向图。如顶点集V可分割为两个互不相交的子集，并且图中每条边依附的两个顶点都分属两个不同的子集。则称图G为二分图。我们将上边顶点集合称为VX​集合，下边顶点结合称为VY​给定一个二分图G，在G的一个子图M中，M的边集E中的任意两条边都不依附于同一个顶点，则称M是一个匹配。如下，在子图中两条边都不依附同一个顶点，因此它是G。
DETR二分图匹配
teletubbies的博客
03-26 1051
即遍历所有预测框，将预测框和所有真实框计算loss，然后将loss放入cost matrix，有了loss，我们便可以使用Linear sum assignment（匈牙利算法）得到最优解。我们知道这100个框中哪几个框和ground truth框是对应的，接下来，我们可以算真正的目标函数，然后用这个loss做梯度回传。例如我们有三个工人abc，我们需要完成三个工作xyz，因为每个工人有各自的长处短处，所以，完成工作所需要的时间和工钱也不一样。其包含两部分，一个是分类损失，一个是框的准确率损失。
【计算机视觉 | 目标检测】术语理解7：二值匹配（Binary Matching），DETR中的Object query的理解，匈牙利算法，DETR中的二分图匹配
wzk4869的博客
06-29 7513
【计算机视觉 | 目标检测】术语理解7：二值匹配（Binary Matching），DETR中的Object query的理解，匈牙利算法，DETR中的二分图匹配
DETR中的匈牙利算法：结合图文例子详解
最新发布
weixin_44115575的博客
09-25 1392
摘要：本文系统介绍了匈牙利算法在DETR目标检测器中的关键应用。首先阐述了DETR需要匹配机制的原因：通过固定数量的预测框与真实目标建立最优对应，替代传统NMS后处理。详细解析了匈牙利算法的核心原理，包括行减、列减、最小覆盖线等矩阵操作步骤，并通过示例图解说明匹配过程。特别指出DETR中未匹配的预测会被自动归类为"noobject"，实现端到端训练。最后总结了该算法对DETR架构的重要意义及其在各改进模型中的持续应用价值。
通过公式和源码解析 DETR 中的损失函数 & 匈牙利算法（二分图匹配）
热门推荐
Flying Bulldog 的博客
07-26 1万+
DETR在单次通过解码器时推断一个固定大小的有N个预测的集合，其中N被设置为显著大于图像中典型的物体数量。所有真实框中的每一个框和所有预测框进行匹配，损失值最小的预测框为该真实框的最佳匹配框，当所有真实框遍历完毕后，得到所有唯一匹配的框。完成最优分配，假设有六位老师和六种课程，通过匈牙利算法进行匹配后，每一位老师都会分到不同的一个课程。匹配成功之后，对预测框的分数、类别、中心点坐标和宽高进行损失值的计算。之间的匹配成本并不依赖于预测，这意味着在这种情况下，成本是一个常数。表示有N个预测的集合。...
DETR代码学习（五）之匈牙利匹配
pengxiang1998的博客
04-04 9552
匈牙利匹配先前在损失函数那块已经介绍过，但讲述了并不清晰，而且准确来说，匈牙利匹配所用的cost值与损失函数并没有关系，因此今天我们来看一下匈牙利匹配这块的代码与其原理。前面已经说过，DETR将目标检测看作集合预测问题，在最后的预测值与真实值匹配过程，其实可以看做是一个二分图匹配问题，该问题的解决方法便是匈牙利算法。
二分图匹配(匈牙利算法)
退役的熬夜选手
09-11 370
二分图匹配 有两个集合A,B 现在知道A中的某些元素可以和B中的某些元素连接(同一个元素可能可以连接多个元素) 现要求最大的匹配数(最多有多少对Ax和Bx可以完成匹配) #include<iostream> #include<cstring> #include<cstdio> using namespace std; const int maxn = 1005;...
匈牙利算法详解 - DETR中的应用
ningaiiiii的博客
03-11 1495
匈牙利算法详解 - DETR中的应用
DETR学习分享：匈牙利Hungarian算法介绍
钱多多先森
06-30 1万+
match.py部分完整代码，如下： # Copyright (c) Facebook, Inc. and its affiliates. All Rights Reserved """ Modules to compute the matching cost and solve the corresponding LSAP. """ import torch from scipy.optimize import linear_sum_assignment from torch import nn ..
DINO-DETR匈牙利匹配与加噪过程学习记录
pengxiang1998的博客
06-17 1556
今天再来回顾一下DINO中匈牙利匹配与损失函数部分，该部分大致与DETR相似，却又略有不同。为了查看数据方便，博主将num_query改为20，max_select值也为20。
DETR中的匈牙利算法的意义
weixin_52056073的博客
12-09 1396
在 DETR 中，匈牙利算法的主要作用是解决目标匹配问题，即将模型的预测框与真实框进行最优匹配，基于此计算损失并进行反向传播。匈牙利算法通过最小化代价矩阵中的总代价，确保每个预测框与对应的真实框进行匹配，并基于匹配结果计算分类损失和回归损失，从而引导网络学习更精确的目标检测任务。C_%7Bij%7D。
DETR纯代码分享（十）matcher.py(models)匈牙利匹配算法
sinat_41942180的博客
10-09 2317
匈牙利匹配算法
DETR | 基于匈牙利算法的样本分配策略
Clichong
06-19 1万+
如有错误，恳请指出。前不久，沐神对DETR进行了讲解，其实之前也对DETR进行了介绍，见：论文阅读笔记 | 目标检测算法——DETR。现对DETR的核心内容进行重温，也就是其所提出的目标检测的end-to-end框架，输入的是一张图像，输出的直接是最后的预测标注结果，不再需要后处理（nms非极大值抑制）。为什么希望end-to-end，是因为nms对于模型的调参比较复杂。而且因为不是所有的硬件都支持这nms，所有即使训练好了模型，部署起来也比较困难。DETR既不需要proposal，也不需要anchor，直
DETR匈牙利匹配bipartite matching loss的思考：未匹配的预测框仅计算分类损失
Hali_Botebie的博客
06-16 1181
关于DETR中的流程图DETR最后一张图片，真值有2个bounding box（框，简称：bbox），DETR中会固定预测出100个bbox框（预测的结果包含框的位置、大小以及框中目标具体类别）。推理时相对简单：100个bbox集合在推理阶段通过0.7的阈值进行区分。大于阈值认为是前景图，也就是那几只海鸟，小于阈值bbox是no object 背景图。训练时的计算比较复杂，设计到匹配问题，真值有2个bbox，但是预测了100个bbox，怎样建模和计算这100个bbox和真值的loss？
匈牙利算法在DETR中应用
weixin_42581846的博客
01-06 264
匈牙利算法是一种用于在图中寻找最大匹配的算法。在DETR (End-to-End Object Detection with Transformers)中，匈牙利算法被用来将图像中的对象与边框匹配，从而帮助定位图像中的对象。DETR是一种基于Transformer架构的端到端目标检测模型，它使用图卷积网络来生成图像中对象的边框，然后使用匈牙利算法来匹配图像中的对象。这样，DETR可以在一张图像中识...
一文读懂DETR中的匈牙利算法
2501_90323865的博客
05-30 246
匈牙利算法被认为是解决分配问题的高效方法，该问题涉及在给定成本的情况下，为一组任务找到最佳的分配给一组执行者的方案。其流程从构建成本矩阵开始，矩阵中的每个元素代表将一个工作者分配去完成一项任务的成本。接着进行行约简，即从每行的所有元素中减去该行的最小元素；然后进行列约简，对列执行类似的操作。之后，目标是用最少数量的水平和垂直直线覆盖矩阵中的所有零元素。通过检查覆盖直线的数量是否等于矩阵的大小来判断最优性：若相等，则存在最优分配；
DETR匈牙利匹配损失：端到端目标检测的核心实现与优化指南
燃灯工作室
02-20 664
工业落地时优先选择Deformable DETR变体，在保持精度的同时显著提升推理速度。关注查询初始化策略对特定场景的适配性，可通过可视化匹配过程诊断模型行为。将预测结果与真实标签一一对应，消除传统NMS后处理，实现真正的端到端检测。：λ_cls=2, λ_L1=5, λ_giou=2（COCO数据集）
完美匹配-匈牙利算法
salmonwilliam的博客
05-16 528
https://blog.youkuaiyun.com/lady_killer9/article/details/103586834
采用二分图匹配损失（匈牙利算法）
08-09
### 二分图匹配与损失计算 二分图匹配是一种经典的图论问题，其目标是在一个二分图中找到一组边，使得每条边连接图的两个不同部分中的顶点，并且没有两个边共享同一个顶点。匈牙利算法是一种用于解决二分图最大匹配问题的经典算法。在任务分配或目标跟踪等应用中，二分图匹配可以用于将预测结果与真实值进行最优匹配，从而计算损失函数以指导模型训练。 ### 匈牙利算法的基本原理 匈牙利算法的核心思想是通过寻找增广路径来增加匹配的大小。算法的基本流程如下： 1. **初始化**：从一个空匹配开始。 2. **寻找增广路径**：对于每个未匹配的顶点，尝试找到一条增广路径，即一条从该顶点出发的路径，其边交替出现在匹配中和不在匹配中，并且终点是一个未匹配的顶点。 3. **更新匹配**：一旦找到增广路径，就将路径上的匹配边和非匹配边互换，从而增加匹配的数量。 4. **重复步骤2和3**，直到不能再找到增广路径为止。 通过这种方式，匈牙利算法能够在多项式时间内找到二分图的最大匹配。 ### 匈牙利算法在损失计算中的应用 在DETR（Detection Transformer）模型中，匈牙利算法被用于解决预测框和真实框之间的最优匹配问题。DETR是一种基于Transformer的目标检测模型，它直接输出一组预测框，并通过匈牙利算法找到这些预测框与真实框之间的最佳匹配。这种匹配方式确保了每个预测框只与一个真实框配对，并且整体匹配是最优的。 损失计算通常包括两个部分：分类损失和位置损失。分类损失衡量预测类别与真实类别的差异，而位置损失衡量预测框与真实框之间的几何差异。由于预测框和真实框之间存在一一对应的关系，因此可以使用匈牙利算法来确定这种对应关系。 ### 实现基于匈牙利算法的损失计算 以下是一个简单的Python代码示例，展示了如何使用匈牙利算法来计算二分图匹配的损失： ```python import numpy as np from scipy.optimize import linear_sum_assignment def compute_loss(predictions, targets): """ 计算基于匈牙利算法的二分图匹配损失。 参数: predictions (np.ndarray): 预测框，形状为 (num_predictions, 4) targets (np.ndarray): 真实框，形状为 (num_targets, 4) 返回: float: 总损失值 """ # 计算预测框与真实框之间的距离矩阵 cost_matrix = np.zeros((len(predictions), len(targets))) for i, pred in enumerate(predictions): for j, target in enumerate(targets): # 使用欧氏距离作为成本 cost_matrix[i, j] = np.linalg.norm(pred - target) # 使用匈牙利算法找到最优匹配 row_ind, col_ind = linear_sum_assignment(cost_matrix) # 计算总损失 total_loss = cost_matrix[row_ind, col_ind].sum() return total_loss # 示例数据 predictions = np.array([[1.0, 2.0, 3.0, 4.0], [2.0, 3.0, 4.0, 5.0], [3.0, 4.0, 5.0, 6.0]]) targets = np.array([[1.1, 2.1, 3.1, 4.1], [2.2, 3.2, 4.2, 5.2]]) loss = compute_loss(predictions, targets) print(f"Total Loss: {loss}") ``` ### 任务分配与目标跟踪中的应用 在任务分配问题中，匈牙利算法可以用于将任务分配给不同的执行者，使得总成本最小。在目标跟踪中，匈牙利算法可以用于将当前帧中的检测结果与前一帧中的跟踪目标进行匹配，从而实现目标的连续跟踪。 ### 总结 匈牙利算法是一种高效的二分图匹配算法，广泛应用于任务分配、目标跟踪等领域。通过将预测结果与真实值进行最优匹配，匈牙利算法可以帮助计算损失函数，从而指导模型的训练过程。在实际应用中，可以通过计算预测框与真实框之间的距离矩阵，并使用匈牙利算法找到最优匹配，进而计算损失值。
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值