C++递推

最新推荐文章于 2024-11-01 12:56:39 发布

Zcy_2010

最新推荐文章于 2024-11-01 12:56:39 发布

阅读量489

点赞数 9

CC 4.0 BY-SA版权

文章标签： c++

本文链接：https://blog.youkuaiyun.com/Zcy_2010/article/details/136437790

第一题、

#include<bits/stdc++.h>
using namespace std;
int main()
{
	int a[110]={0};
	int b[110]={0};
	int c[110]={0};
	a[1]=0;
	b[1]=1;
	c[1]=0;
	int n;
	cin>>n;
	for(int i=2;i<=n;i++)
	{
		a[i]=a[i-1]+c[i-1];
		b[i]=a[i];
		c[i]=b[i-1];
	}
	cout<<a[n]+b[n]+c[n]<<endl;
	return 0;
}

第二题、

#include<bits/stdc++.h>
using namespace std;
int main()
{
	int a[20]={0};
	a[10]=1;
	for(int i=9;i>=1;i--)
	{
		a[i]=(a[i+1]+1)*2;
	}
	cout<<a[1]<<endl;
	return 0;
}

第三题、

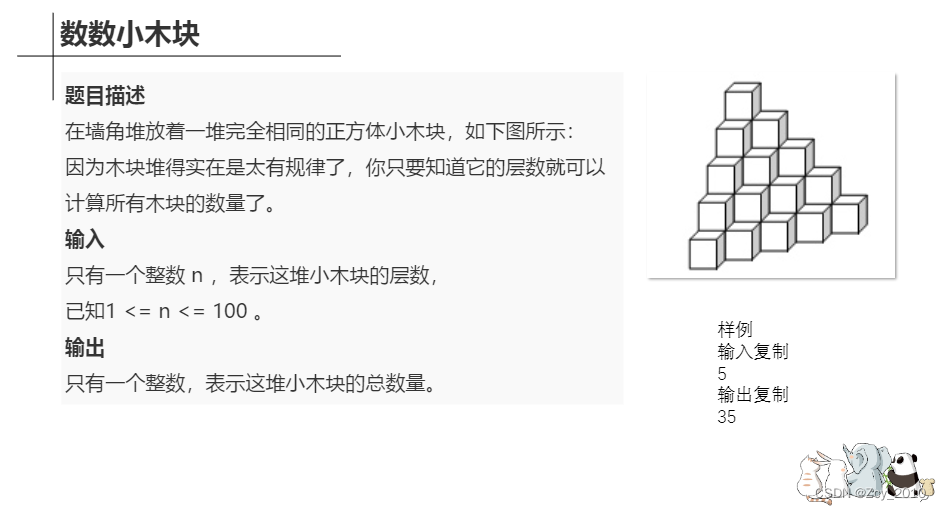
#include<bits/stdc++.h>
using namespace std;
int main()
{
    int a[110]={0};
	int b[110]={0};
	a[1]=1;
	b[1]=a[1];
	int n;
	cin>>n;
	for(int i=2;i<=n;i++)
	{
		a[i]=a[i-1]+i;
		b[i]=b[i-1]+a[i];
	}
	cout<<b[n]<<endl;
	return 0;
}

第四题、

#include<bits/stdc++.h>
using namespace std;
int main()
{
	long long a[1100]={0};
	a[1]=1;
	a[2]=2;
	int n;
	cin>>n;
	for(int i=3;i<=n;i++)
	{
		a[i]=a[i-1]*2+a[i-2];
	}
	cout<<a[n]<<endl;
	return 0;
}

第五题、

#include<bits/stdc++.h>
using namespace std;
int main()
{
	int a[100]={0};
	a[1]=1;
	a[2]=2;
	a[3]=4;
	for(int i=4;i<=30;i++)
	{
		a[i]=a[i-1]+a[i-2]+a[i-3];
	}
	while(true)
	{
		int n;
		cin>>n;
		if(n==0)
		{
			break;
		}
		else
		{
			cout<<a[n]<<endl;
		}
	}
	return 0;
}

第六题、

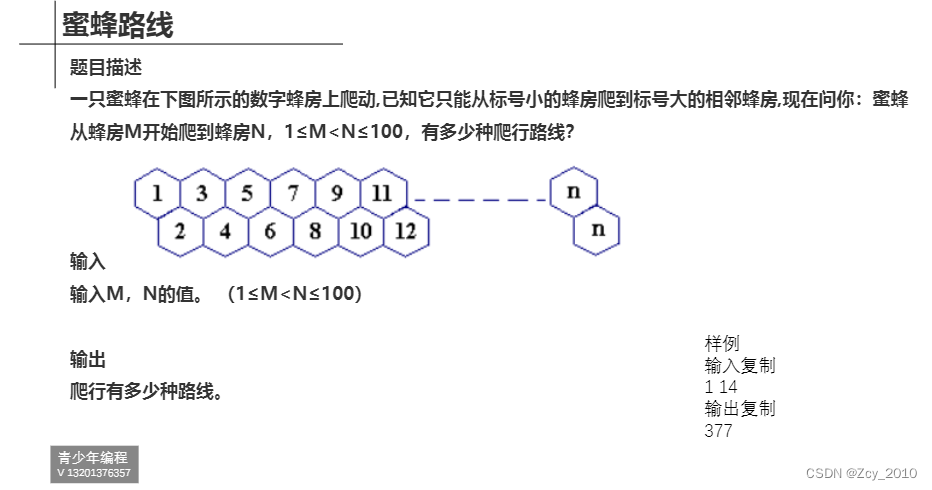
#include<bits/stdc++.h>
using namespace std;
int main()
{
	int a[110]={0};
	a[1]=1;
	a[2]=1;
	int M,N;
	cin>>M>>N;
	for(int i=3;i<=N-M+1;i++)
	{
		a[i]=a[i-1]+a[i-2];
	}
	cout<<a[N-M+1]<<endl;
	return 0;
}

第七题、

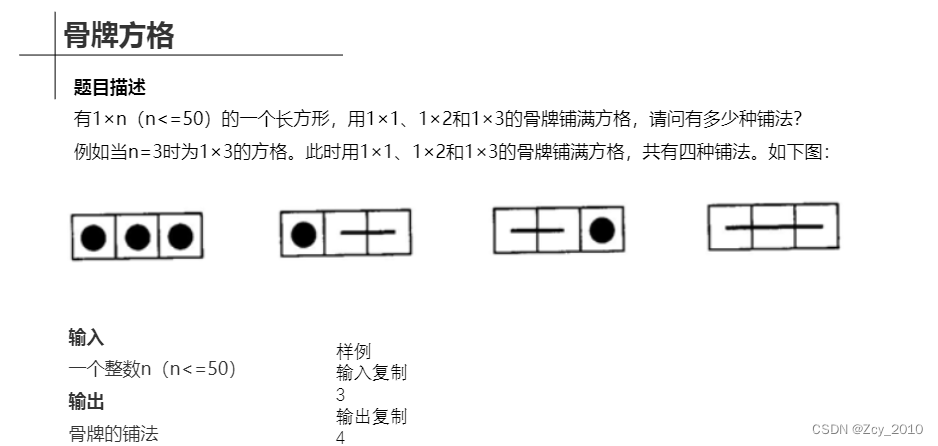
#include<bits/stdc++.h>
using namespace std;
int main()
{
	int a[60]={0};
	a[1]=1;
	a[2]=2;
	a[3]=4;
	int n;
	cin>>n;
	for(int i=4;i<=n;i++)
	{
		a[i]=a[i-1]+a[i-2]+a[i-3];
	}
	cout<<a[n]<<endl;
	return 0;
}