本文探讨了一种优化的编程解法，通过四维动态规划策略，解决了2021年6月2日的Luogu竞赛题目，涉及矩阵路径问题与最大和路径选择。首先介绍了错误的深度优先搜索思路，然后详细解析了二维DP的局限并转向三维dp，成功找到了两次取数路径使和最大。最后，展示了如何通过三维状态转移方程求解传纸条问题，最大化路径上的好感度总和。
2021.06.02两次矩阵取数+传纸条
(题目来源：https://www.luogu.com.cn/problem/P1004 )
题目描述
设有 N ×\times× N 的方格图 (N≤9N \le 9N≤9)，我们将其中的某些方格中填入正整数，而其他的方格中则放入数字 0。如下图所示（见样例）:
A
0 0 0 0 0 0 0 0
0 0 13 0 0 6 0 0
0 0 0 0 7 0 0 0
0 0 0 14 0 0 0 0
0 21 0 0 0 4 0 0
0 0 15 0 0 0 0 0
0 14 0 0 0 0 0 0
0 0 0 0 0 0 0 0
B
某人从图的左上角的 A 点出发，可以向下行走，也可以向右走，直到到达右下角的 B 点。在走过的路上，他可以取走方格中的数（取走后的方格中将变为数字 0）。
此人从 A 点到 B 点共走两次，试找出 2 条这样的路径，使得取得的数之和为最大。
输入格式
输入的第一行为一个整数 N（表示 N×NN \times NN×N 的方格图），接下来的每行有三个整数，前两个表示位置，第三个数为该位置上所放的数。一行单独的 0 表示输入结束。
输出格式
只需输出一个整数，表示 2 条路径上取得的最大的和。
样例输入
8
2 3 13
2 6 6
3 5 7
4 4 14
5 2 21
5 6 4
6 3 15
7 2 14
0 0 0
样例输出
67
思路
【错误】思路：两次dp
-
一开始考虑深度优先搜索，但是由于复杂度达到2^81 * 2^81次，所以放弃。
-
考虑两次dp，每次都取最优。
-
由于第一次dp影响第二次，所以开辟一个容器存储第一次遍历到最优时的所有点坐标。
-
由于每次找dp都只和当前上一行元素和当前左边元素有关，所以开辟容器只需要开辟一个一维数组。（其实dp矩阵也是如此），说明如下：
-
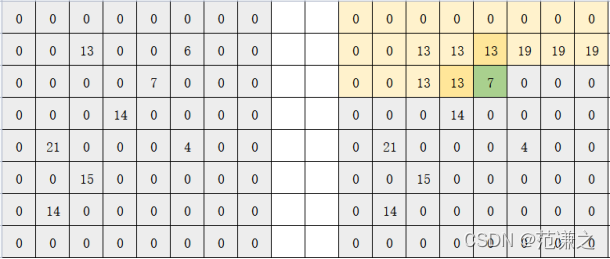
该方法仅对于部分数据可以通过，
代码
class Solution{
int res = 0;
List<String> dic = new ArrayList<String>();
String s;
void test() {
//dp[i][j] = map[i][j]+Max( dp[i-1][j], dp[i][j-1] )
//记录状态，dp[i]对应的走过哪些点( List(x,y) )
Scanner cin = new Scanner(System.in);
int n = cin.nextInt();
int[][] map = new int[n+1][n+1];
int[][] dp = new int[n+1][n+1];
HashSet<List<Integer>>[] ps = new HashSet[n+1];
for(int i = 0; i < ps.length; i++) {
ps[i] = new HashSet<List<Integer>>();
}
while(true) {
int i = cin.nextInt();
int j = cin.nextInt();
int v = cin.nextInt();
if(i==0&&j==0) break;
map[i][j] = v;
}
int res = 0;
for(int i = 1; i <= n; i++) {
for(int j = 1; j <= n; j++) {
if(dp[i][j-1] >= dp[i-1][j]) { //如果左边 >= 上面，采用左边的容器
ps[j] = new HashSet<List<Integer>>(ps[j-1]);
dp[i][j] = map[i][j] + dp[i][j-1];
} else {
ps[j] = new HashSet<List<Integer>>(ps[j]);
dp[i][j] = map[i][j] + dp[i-1][j];
}
if(map[i][j] != 0) {//如果本位置价值大于0，一定装入容器
List<Integer> lis = new ArrayList<Integer>();
lis.add(i); lis.add(j);
ps[j].add(lis);
}
}
}
res += dp[n][n];
for(List<Integer> lis: ps[n])
map[lis.get(0)][lis.get(1)] = 0;
for(int i = 1; i <= n; i++)
for(int j = 1; j <= n; j++)
dp[i][j] = Math.max(dp[i-1][j], dp[i][j-1])+map[i][j];
res += dp[n][n];
System.out.println(res);
}
}
【正确】思路1：四维dp
- 定义状态:
dp[i][j][k][l]: 第一次走到(i,j)位置，第二次到(k,l)位置。 - 状态转移：
对于状态dp[i][j][k][l]，有四种可能的到达方法：
（1）第一次从(i,j-1)往右 && 第二次从(k,l-1)往右
（2）第一次从(i-1,j)往下 && 第二次从(k-1,l)往下
（3）第一次从(i,j-1)往右 && 第二次从(k-1,l)往下
（4）第一次从(i-1,j)往下 && 第二次从(k,l-1)往右
由于两次走到同一个方格的价值只能取一次，所以添加判断，当(i,j) == (k,l)
代码
class Solution{
int res = 0;
List<String> dic = new ArrayList<String>();
String s;
void test() {
Scanner cin = new Scanner(System.in);
int n = cin.nextInt();
int[][] map = new int[n+1][n+1];
//定义状态：dp[i][j][k][l] 为第一次走到(i,j)，第二次走到(k,l)处的最佳策略
int[][][][] dp = new int[n+1][n+1][n+1][n+1];
while(true) {
int i = cin.nextInt();
int j = cin.nextInt();
int v = cin.nextInt();
if(i==0&&j==0) break;
map[i][j] = v;
}
//前言：置零操作体现在dp状态中，而非在矩阵map中。
for(int i = 1; i <= n; i++) {
for(int j = 1; j <= n; j++) {
for(int k = 1; k <= n; k++) {
for(int l = 1; l <= n; l++) {
//没有将走过的路径置0操作，是因为：
//对于dp[i][j-1][k][l-1],dp[i][j-1][k-1][l],dp[i-1][j][k][l-1], dp[i][j-1][k-1][l]
//这四个状态，在其前面遍历过程中，如果走到统一个方格，已经减了value值，所以相当于置零操作。
dp[i][j][k][l] = Math.max(Math.max(dp[i][j-1][k][l-1], dp[i][j-1][k-1][l]),
Math.max(dp[i-1][j][k][l-1], dp[i-1][j][k-1][l]))+map[i][j]+map[k][l];
if(i==k&&j==l) dp[i][j][k][l] -= map[i][j]; //
}
}
}
}
System.out.println(dp[n][n][n][n]);
}
}
代码
传纸条
(题目来源：https://www.luogu.com.cn/problem/P1006 )
题目描述
小渊和小轩是好朋友也是同班同学，他们在一起总有谈不完的话题。一次素质拓展活动中，班上同学安排坐成一个 m 行 n 列的矩阵，而小渊和小轩被安排在矩阵对角线的两端，因此，他们就无法直接交谈了。幸运的是，他们可以通过传纸条来进行交流。纸条要经由许多同学传到对方手里，小渊坐在矩阵的左上角，坐标 (1,1)，小轩坐在矩阵的右下角，坐标 (m,n)。从小渊传到小轩的纸条只可以向下或者向右传递，从小轩传给小渊的纸条只可以向上或者向左传递。
在活动进行中，小渊希望给小轩传递一张纸条，同时希望小轩给他回复。班里每个同学都可以帮他们传递，但只会帮他们一次，也就是说如果此人在小渊递给小轩纸条的时候帮忙，那么在小轩递给小渊的时候就不会再帮忙。反之亦然。
还有一件事情需要注意，全班每个同学愿意帮忙的好感度有高有低（注意：小渊和小轩的好心程度没有定义，输入时用 0 表示），可以用一个 [0,100] 内的自然数来表示，数越大表示越好心。小渊和小轩希望尽可能找好心程度高的同学来帮忙传纸条，即找到来回两条传递路径，使得这两条路径上同学的好心程度之和最大。现在，请你帮助小渊和小轩找到这样的两条路径。
输入格式
第一行有两个用空格隔开的整数 m 和 n，表示班里有 m 行 n 列。
接下来的 m 行是一个 m×nm \times nm×n 的矩阵，矩阵中第 i 行 j 列的整数表示坐在第 i 行 j 列的学生的好心程度。每行的 nn 个整数之间用空格隔开。
输出格式
输出文件共一行一个整数，表示来回两条路上参与传递纸条的学生的好心程度之和的最大值。
样例输入
3 3
0 3 9
2 8 5
5 7 0
样例输出
34
数据规模和约定
对于 30% 的数据，1≤m,n≤10；
对于 100% 的数据满足：1≤m,n≤50。
【优化】思路2：三维dp
1.换一种思路看本题，如果不看成走两次，而是看成两个人同时走，效果是一样的。但是，这种思路为i,j,k,l添加了限定规则，即i+jk+lstep（因为两个人只能向下和向右） 。
2.可以重新定义状态：
dp[s][i][j]:此时走了s步，一个人走到了(i,s-i)，另一个走到了(j,s-j)
3.状态转移方程：
仍是由下图得出：
dp[s][i][j] = Max{ dp[s-1][i-1][j-1], dp[s-1][i-1][j], dp[s-1][i][j-1], dp[s-1][i][j] }
代码
class Solution{
int res = 0;
List<String> dic = new ArrayList<String>();
String s;
int maxEle(int i,int j, int k, int l) {
return Math.max(Math.max(i, l), Math.max(j, k));
}
void test() {
Scanner cin = new Scanner(System.in);
int m = cin.nextInt();
int n = cin.nextInt();
int[][] map = new int[m+1][n+1];
//定义状态：dp[s][i][j]：步数s，行数i，j
int[][][] dp = new int[n+m+1][m+1][m+1];
for(int i = 1; i <= m; i++) for(int j = 1; j <= n; j++) map[i][j] = cin.nextInt();
for(int s = 1; s <= m+n-1; s++)
for(int i = 1; i <= Math.min(s, m); i++) //所在的行数不可能超过步数
for(int j = 1; j <= Math.min(s, m); j++) {
if(s+1-i>n||s+1-j>n) continue; //如果纵坐标越界
dp[s][i][j] = maxEle(dp[s-1][i-1][j-1], dp[s-1][i-1][j], dp[s-1][i][j-1], dp[s-1][i][j])
+map[i][s+1-i]+map[j][s+1-j];
if(i==j) dp[s][i][j] -= map[i][s+1-i];
}
System.out.println(dp[m+n-1][m][m]);
}
}
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
