地震资料处理——（六）地震水平叠加

水平叠加处理

假设一个共中心点道集有三个地震道，经过速度分析和动校正以后，水平叠加以后有效波会得到增强，随机干扰得到相对的削弱：

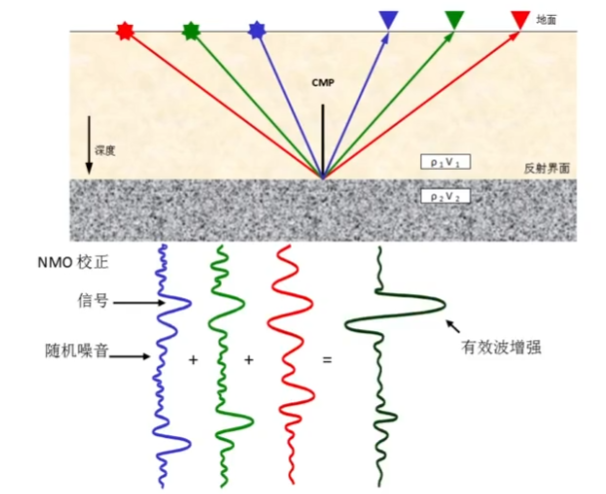
动校正后浅层会有畸变，畸变切除后就可以水平叠加：

共中心点道集经过动校正后叠加起来，每一个共中心点道集叠加以后就变成了一道：

把水平叠加以后的道紧凑的排列起来，横轴是测线方向的地面坐标，纵轴是反射波的双程旅行时：

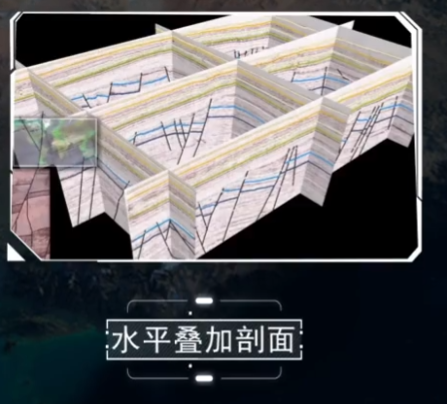
每一个共中心点道集都这么处理，直到把一条侧线上所有的共中心点都处理完，最终可以得到比较真实反应地下地层形态的水平叠加剖面：

水平叠加处理提高信噪比的证明：
设水平叠加后的总输出$F(t)$为动校正后隔道地震波$f(t-\delta t_k)$的叠加，隔道地震波的波形没有变化，隔道只存在剩余时差$\delta t_k$，其中$k=1，2，3\cdots ,n$，$n$为地震多次覆盖的次数。那么水平叠加后的频谱$F(\omega )$等于无剩余时差$f(t)$的频谱$f(\omega )$与$K(\omega )$相乘，在频率域中，水平叠加后的输出相当于做了一次滤波，滤波器为$K(\omega )$：

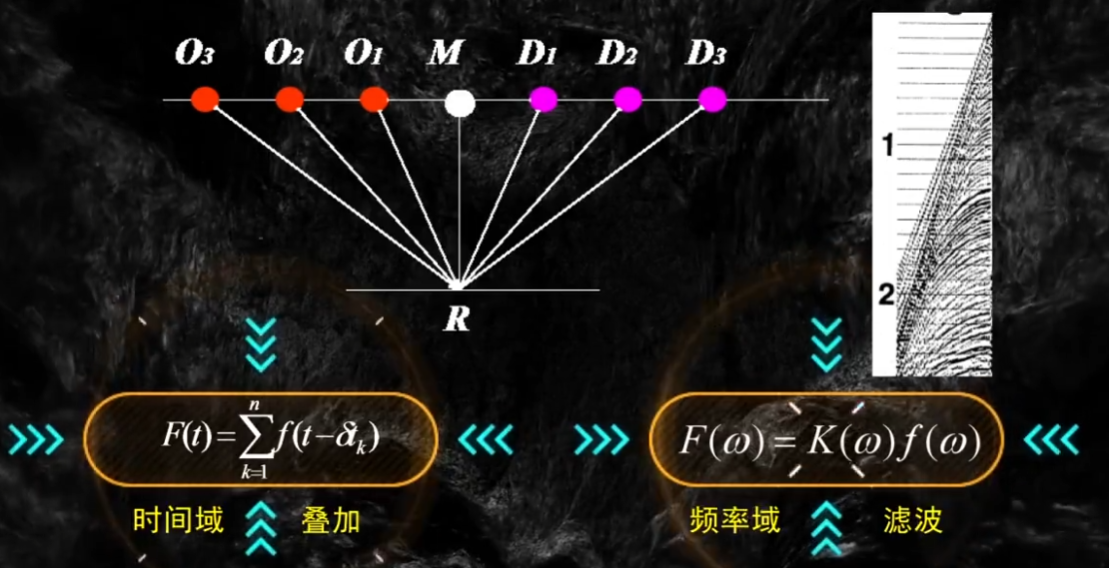
根据傅里叶变换的时延定律，可以得到滤波器$K(\omega )$的指数求和的表达式，这个滤波器就称为叠加特性函数，叠加特性的振幅特性函数也可以用正弦、余弦特性函数表示：

对叠加特性函数进行归一化处理得到$P(\omega )$，分析$P(\omega )$可以得到：一次反射波经过动校正以后，不存在剩余时差$\delta t_k=0$，叠加特性函数的值为1，这样有效波就得到加强；多次波这样的干扰波在用一次波进行动校正以后，还存在剩余时差$\delta t_k$，叠加特性的值是小于1的，干扰波就相对得到压制：

将剩余时差$\delta t_k$除以地震波的周期，可以得到一个与多次覆盖系统相关的量${\alpha }_k$，已知多次覆盖系统观测参数，就可以得到多次叠加振幅特性曲线$P({\alpha }_k)$，只要合理设计地震野外观测系统参数，就可以让一次反射波在通放带通过，让存在剩余时差的干扰波在压制带被压制：

从多次叠加的频率特性曲线上，可以看到，在设计野外观测系统的时候，不能让通放带太窄：

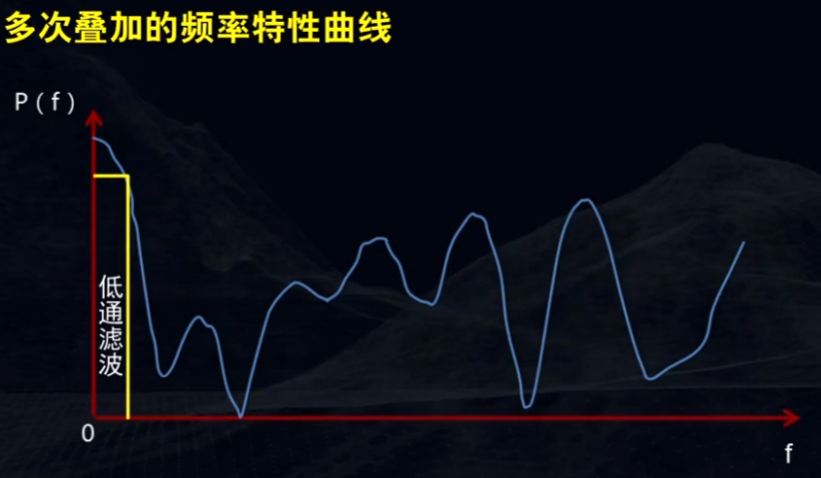
多次覆盖、水平叠加，尽管提高了信噪比，但是由于水平叠加后，频带整体变窄，地震分辨率相对变低了。

水平叠加的统计效应与检波器组合法在数学上遵循同样的原理。当道集内各道炮检距的差值不大于相关半径时，则各道的随机干扰就是互不相关的。n次覆盖后，随机干扰值增强了$\sqrt{n}$倍，而有效波则增强了n倍。所以多次叠加对随机干扰的压制效果优于检波器组合法。

影响水平叠加处理的因素

地震道间距、偏移距和覆盖次数对水平叠加效果也有一定的影响。
随着道间距$\Delta x$的增大，通放带变窄变陡，压制带向左移，有利于压制与一次波相近的多次波这样的干扰波，但$\Delta x$也不应过大，太大会使一次波也受到压制；$\Delta x$过小，则干扰波也处于通放带，不利于压制多次波这样的干扰波：

偏移距不宜过大，太大会使某些规则干扰波进入二次极值区，影响压制干扰波的效果，也会显示浅层的有效波：

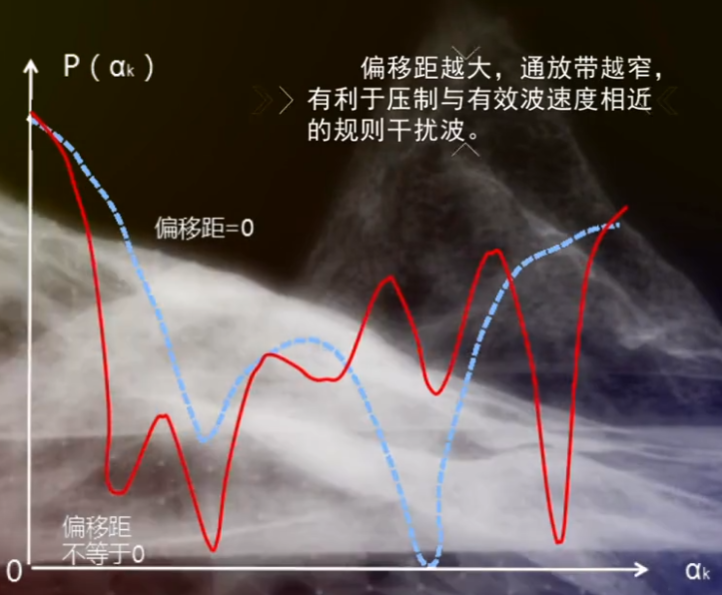
覆盖次数过大，对一些尚存一定时差的有效波不利：

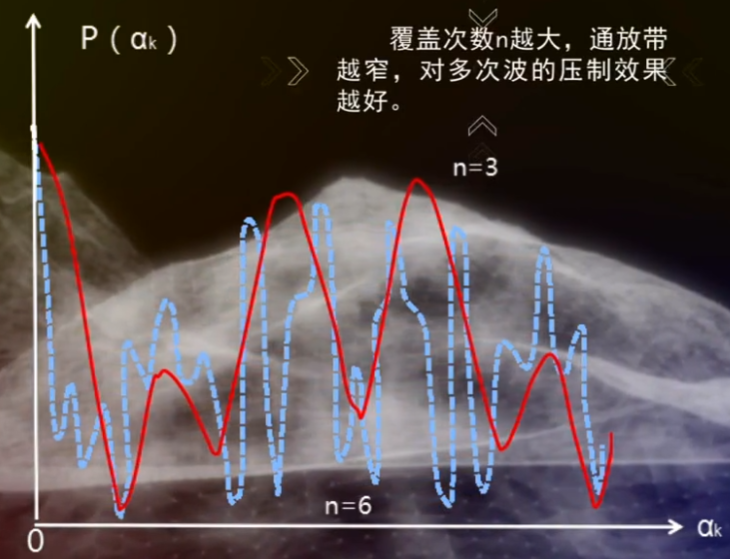
覆盖次数的提高，有利于对地下构造的清晰成像：

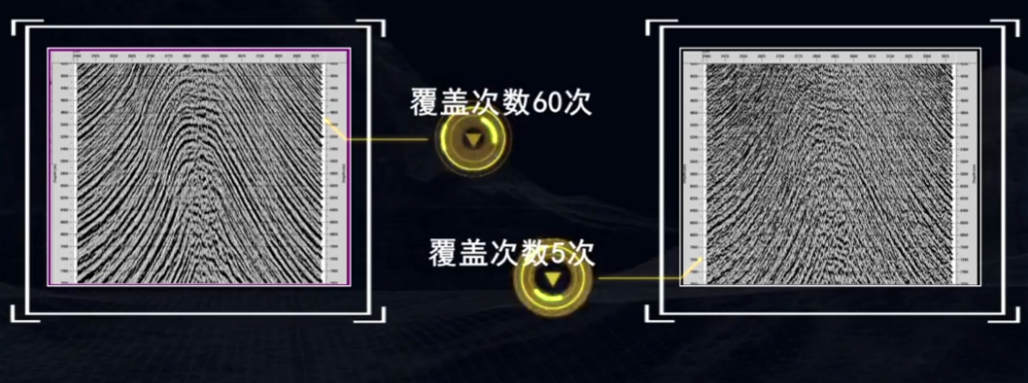
动校正速度对水平叠加效果的影响：


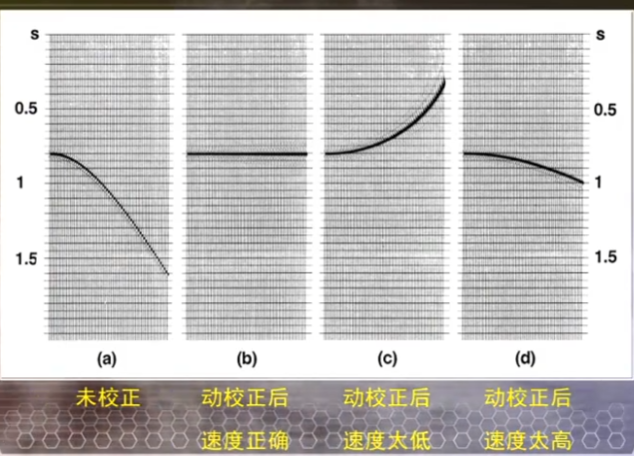
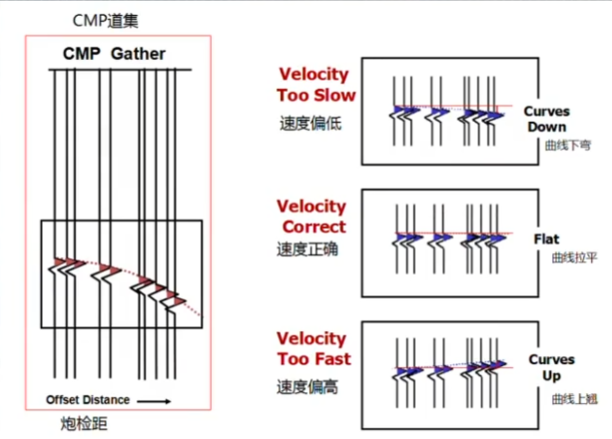
地层倾角对水平叠加效果的影响：


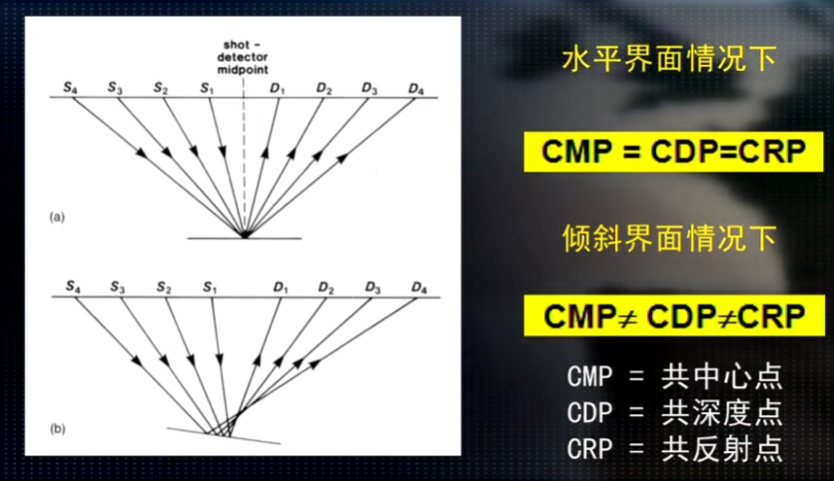
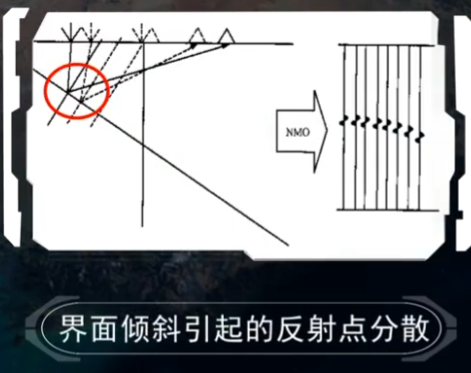
必须进行叠前部分偏移处理：

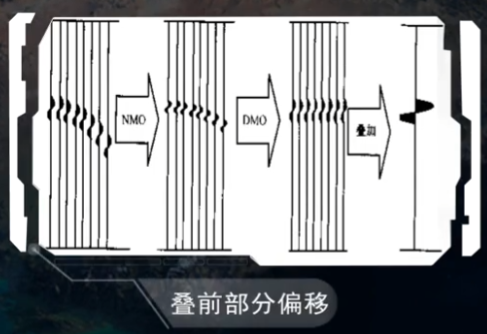
但是DMO校正后反射点的位置与真正的反射点的位置还有一定的偏差，必须应用更好的叠后和叠前偏移的方法让反射点真正的归位：

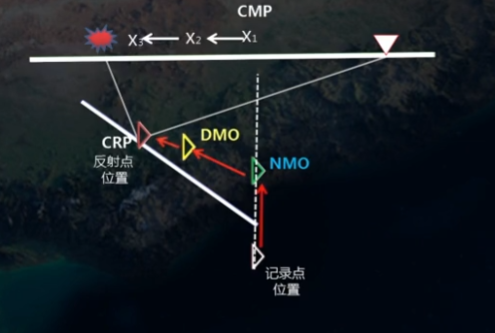
在地下构造复杂，速度横向变化剧烈的情况下，反射波的时距曲线本身就不是双曲线，特别是在三维地震勘探中，反射波的旅行时还与炮检方位角有关，因此无论采用什么动校正速度，可能都不能把时距曲线校成直线，这就会严重影响水平叠加的效果和成像精度。因此，可以采用叠前偏移叠加的其它一些新的方法来取代水平叠加处理。
常规的水平叠加剖面是对共中心点道集内的全波炮检距进行NMO校正后叠加，全炮检距水平叠加剖面不利于储存预测和油气检测。

因此在常规水平叠加基础上，有人提出了角度叠加（或称为部分角度叠加）：

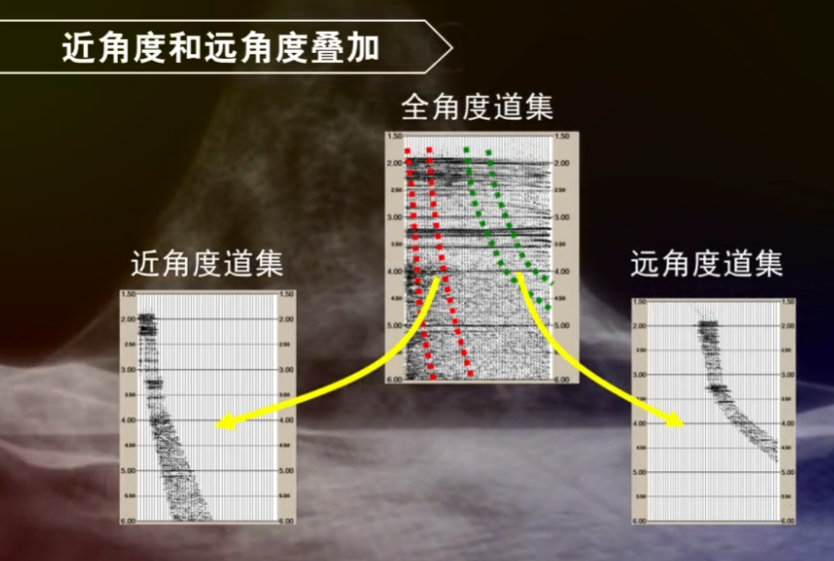
在部分角度叠加剖面上，可以解释出全叠加剖面上没有的地质或含油气的特征。