【动态规划dp问题】——leetcode关于买卖股票的最佳时期系列问题

UnRuins

已于 2024-12-10 18:41:02 修改

阅读量832

点赞数 20

CC 4.0 BY-SA版权

分类专栏：算法题文章标签：动态规划 leetcode 算法

于 2024-12-10 18:39:48 首次发布

本文链接：https://blog.youkuaiyun.com/ZWW_zhangww/article/details/144379846

算法题专栏收录该内容

17 篇文章

订阅专栏

文章目录

买卖股票的最佳时期
买卖股票的最佳时期2
买卖股票的最佳时期含冷冻期
买卖股票的最佳时期含手续费
买卖股票的最佳时期3
买卖股票的最佳时期4

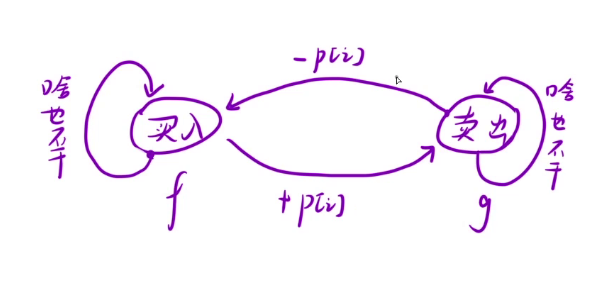
所有的关于只有买入和卖出的问题，都可以通过下面这张图片进行书写dp状态转移方程！如果含有冷冻期也是如此加上冷冻期即可！

在这里插入图片描述

买卖股票的最佳时期

问题: 只能进行一次买卖，求最大利润。
思路:
记录历史最低点 min_price。
遍历数组，计算当前价格与 min_price 的差值作为潜在利润，更新最大利润 max_profit。
时间复杂度
O(n)。
在这里插入图片描述

class Solution 
{
public:
    int maxProfit(vector<int>& prices) 
    {
        int n = prices.size();
        if (n == 0) return 0; // 如果没有价格数据，返回0

        int minPrice = INT_MAX; // 记录历史最低价格
        int maxProfit = 0; // 最大利润

        for (int i = 0; i < n; i++) 
        {
            // 更新历史最低价格
            minPrice = min(minPrice, prices[i]);
            // 计算当前利润并更新最大利润
            maxProfit = max(maxProfit, prices[i] - minPrice);
        }

        return maxProfit; // 返回最终结果
    }
};

买卖股票的最佳时期2

问题: 可以进行无限次买卖，但不能同时进行多笔交易（必须先卖出再买入）。
思路:
只需关注所有上升区间的利润。
遍历数组，累计每次 prices[𝑖+1]>prices[𝑖]的差值。
时间复杂度 O(n)。

在这里插入图片描述

class Solution 
{
public:
    int maxProfit(vector<int>& prices) 
    {
        // 获取股票价格数组的长度
        int n = prices.size();
        // 如果价格数组为空，则直接返回0（没有利润可赚）
        if (n == 0) return 0;

        // 初始化两个变量：f 和 g
        // f 表示持有股票时的最大利润
        // g 表示不持有股票时的最大利润
        int f = 0, g = 0;

        // 将初始状态设置为买入第一天的股票
        // 买入股票时的利润是负的，f 初始化为 -prices[0]
        f = -prices[0];

        // 遍历价格数组，从第二天开始
        for(int i = 1; i < n; i++)
        {
            // 计算持有股票的新最大利润
            // 1. 如果继续持有之前的股票，利润保持不变 (f)
            // 2. 如果在当前价格买入股票，利润为 g - prices[i]
            int newf = max(f, g - prices[i]);

            // 计算不持有股票的新最大利润
            // 1. 如果继续保持不持有状态，利润保持不变 (g)
            // 2. 如果在当前价格卖出股票，利润为 f + prices[i]
            int newg = max(g, f + prices[i]);

            // 更新 f 和 g 为计算得到的新值
            f = newf;
            g = newg;
        }

        // 最终返回不持有股票的最大利润，因为卖出后才算利润
        return g;
    }    
};

可以进行无限次交易，但卖出后需要一天冷却。
思路:
定义状态：
dp[i][0]: 第 𝑖 天持有股票的最大利润。
dp[i][1]: 第 𝑖 天不持有股票，且处于冷却期的最大利润。
dp[i][2]: 第 𝑖 天不持有股票，且不处于冷却期的最大利润。
状态转移：
dp[i][0] = max(dp[i-1][0], dp[i-1][2] - prices[i])
dp[i][1] = dp[i-1][0] + prices[i]
dp[i][2] = max(dp[i-1][2], dp[i-1][1])
最终结果为 max(dp[n−1][1],dp[n−1][2])。
时间复杂度 O(n)，空间复杂度可优化为 O(1)。
在这里插入图片描述

class Solution
{
public:
    int maxProfit(vector<int>& prices)
    {
        int n = prices.size(); // 获取价格数组的大小
        vector<vector<int>> dp(n, vector<int>(3)); // 定义一个二维动态规划数组 dp，其中 dp[i][j] 表示第 i 天的状态 j 所能获得的最大利润
        dp[0][0] = -prices[0]; // 初始化第 0 天的买入状态，表示第 0 天买入股票的成本（负值）
        dp[0][1] = 0;          // 初始化第 0 天的冷冻期状态（不操作），利润为 0
        dp[0][2] = 0;          // 初始化第 0 天的卖出状态，利润为 0

        for (int i = 1; i < n; i++) // 从第 1 天开始遍历每一天
        {
            // 状态 0: 买入股票，可能是从前一天的买入状态保持不变，或者从冷冻期状态转变为买入状态
            dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i]);
            
            // 状态 1: 冷冻期，可能是从前一天的冷冻期状态保持不变，或者从卖出状态转变为冷冻期状态
            dp[i][1] = max(dp[i - 1][1], dp[i - 1][2]);
            
            // 状态 2: 卖出股票，必须是从前一天的买入状态转变为卖出状态
            dp[i][2] = dp[i - 1][0] + prices[i];
        }

        // 最后一天的最大利润，可能是冷冻期或卖出状态的最大值
        return max(dp[n - 1][1], dp[n - 1][2]);
    }
};

买卖股票的最佳时期含手续费

问题: 无限次交易，每次交易需支付手续费。
思路:
定义状态：
f[i]: 第 𝑖 天持有股票的最大利润。
g[i]: 第 𝑖 天不持有股票的最大利润。
状态转移：
f[i] = max(f[i-1], g[i-1] - prices[i])
g[i] = max(g[i-1], f[i-1] + prices[i] - fee)
时间复杂度 O(n)，空间复杂度可优化为 O(1)。
在这里插入图片描述

class Solution 
{
public:
    int maxProfit(vector<int>& prices, int fee) 
    {
        // 获取价格数组的长度
        int n = prices.size();

        // 定义两个动态规划数组：
        // f[i] 表示第 i 天持有股票时的最大利润
        // g[i] 表示第 i 天不持有股票时的最大利润
        vector<int> f(n);
        auto g = f;

        // 第一天持有股票的利润为 -prices[0]
        f[0] = -prices[0];

        // 遍历每一天，从第二天开始
        for(int i = 1; i < n; i++)
        {
            // 状态转移方程：
            // 第 i 天持有股票：
            // 1. 继承前一天持有股票的状态 (f[i-1])
            // 2. 前一天不持有股票，并在第 i 天买入 (g[i-1] - prices[i])
            f[i] = max(f[i - 1], g[i - 1] - prices[i]);

            // 第 i 天不持有股票：
            // 1. 继承前一天不持有股票的状态 (g[i-1])
            // 2. 前一天持有股票，并在第 i 天卖出 (f[i-1] - fee + prices[i])
            g[i] = max(g[i - 1], f[i - 1] - fee + prices[i]);
        }

        // 最终返回最后一天不持有股票时的最大利润
        return g[n - 1];
    }
};

买卖股票的最佳时期3

问题: 最多进行两次交易，求最大利润。
思路:
定义状态：f[i][j]: 第 𝑖 天，进行了 𝑗 次交易，并且持有股票的最大利润。
g[i][j]: 第 𝑖 天，进行了 𝑗 次交易，并且不持有股票的最大利润。
状态转移：
f[i][j] = max(f[i-1][j], g[i-1][j] - prices[i])
g[i][j] = max(g[i-1][j], f[i-1][j-1] + prices[i])
( j≥1)
初始条件：
f[0][0] = -prices[0]
g[0][0] = 0
时间复杂度 O(n)，空间复杂度 O(n)，可优化为 O(1)。
在这里插入图片描述

class Solution 
{
public:
    // 定义一个大数值 INF 用于初始化，表示无效状态
    const int INF = 0x3f3f3f3f;

    int maxProfit(vector<int>& prices) 
    {
        // 获取价格数组长度
        int n = prices.size();

        // 如果价格数组为空，直接返回 0（没有利润可赚）
        if(n == 0) return 0;

        // 定义两个二维动态规划数组
        // f[i][j] 表示第 i 天、已经进行了 j 次交易、并且当前持有股票的最大利润
        // g[i][j] 表示第 i 天、已经进行了 j 次交易、并且当前不持有股票的最大利润
        vector<vector<int>> f(n, vector<int>(3, -INF));
        auto g = f;

        // 初始化第 0 天状态
        // f[0][0]: 第一天买入股票
        f[0][0] = -prices[0];
        // g[0][0]: 第一天不操作（没有进行任何交易）
        g[0][0] = 0;

        // 遍历每一天
        for(int i = 1; i < n; i++)
        {
            // 遍历交易次数 j (最多 2 次)
            for(int j = 0; j < 3; j++)
            {
                // 持有股票的状态：
                // 1. 保持前一天的持有状态 (f[i-1][j])
                // 2. 今天买入股票（从不持有状态转为持有）(g[i-1][j] - prices[i])
                f[i][j] = max(f[i - 1][j], g[i - 1][j] - prices[i]);

                // 不持有股票的状态：
                // 1. 保持前一天的不持有状态 (g[i-1][j])
                g[i][j] = g[i - 1][j];

                // 2. 今天卖出股票（从持有状态转为不持有）(f[i-1][j-1] + prices[i])
                // 只有 j >= 1 时，才能进行交易
                if(j >= 1)
                    g[i][j] = max(g[i][j], f[i - 1][j - 1] + prices[i]);
            }
        }

        // 最终结果：所有不持有股票状态的最大值
        int ret = 0;
        for(int j = 0; j < 3; j++)
            ret = max(ret, g[n - 1][j]);

        return ret;
    }
};

买卖股票的最佳时期4

问题: 最多可以进行 𝑘 次交易，求最大利润。
思路:
如果 k≥n/2，等价于无限次交易问题（问题 2）。
否则，使用动态规划：
定义状态：
f[i][j]: 第 𝑖 天，进行了 𝑗 次交易，并且持有股票的最大利润。
g[i][j]: 第 𝑖 天，进行了 𝑗 次交易，并且不持有股票的最大利润。
状态转移：
f[i][j] = max(f[i-1][j], g[i-1][j] - prices[i])
g[i][j] = max(g[i-1][j], f[i-1][j-1] + prices[i])
( j≥1)
时间复杂度 O(n⋅k)，空间复杂度 O(k)（滚动数组优化）。

class Solution 
{
public:
    int maxProfit(int k, vector<int>& prices) 
    {
        // 定义一个较大的无效值 INF，用于初始化
        const int INF = 0x3f3f3f3f; 

        // 获取价格数组长度
        int n = prices.size();

        // 如果价格数组为空，直接返回 0（没有利润可赚）
        if(n == 0) return 0;

        // 如果交易次数 k 大于天数的一半，等效于无限次交易
        k = min(k, n / 2);

        // 定义两个二维动态规划数组
        // f[i][j]: 第 i 天进行了 j 次交易，并且当前持有股票时的最大利润
        // g[i][j]: 第 i 天进行了 j 次交易，并且当前不持有股票时的最大利润
        vector<vector<int>> f(n, vector<int>(k + 1, -INF));
        auto g = f;

        // 初始化第 0 天的状态
        // f[0][0]: 第一天买入股票
        f[0][0] = -prices[0];
        // g[0][0]: 第一天不操作
        g[0][0] = 0;

        // 遍历每一天
        for(int i = 1; i < n; i++)
        {
            // 遍历交易次数 j，从 0 到 k
            for(int j = 0; j <= k; j++)
            {
                // 持有股票的状态：
                // 1. 保持前一天的持有状态 (f[i-1][j])
                // 2. 今天买入股票（从不持有状态转为持有）(g[i-1][j] - prices[i])
                f[i][j] = max(f[i - 1][j], g[i - 1][j] - prices[i]);

                // 不持有股票的状态：
                // 1. 保持前一天的不持有状态 (g[i-1][j])
                g[i][j] = g[i - 1][j];

                // 2. 今天卖出股票（从持有状态转为不持有）(f[i-1][j-1] + prices[i])
                // 只有 j >= 1 时，才能进行交易
                if(j >= 1)
                    g[i][j] = max(g[i][j], f[i - 1][j - 1] + prices[i]);
            }
        }

        // 最终结果：所有不持有股票状态的最大值
        int ret = 0;
        for(int i = 0; i <= k; i++)
            ret = max(ret, g[n - 1][i]);

        return ret;
    }
};