分治与递归

分治与递归

        分治法的设计思想是，将一个难以直接解决的大问题，分割成一些规模较小的相同问题，以便各个击破，分而治之。
     对这k个子问题分别求解。如果子问题的规模仍然不够小，则再划分为k个子问题，如此递归的进行下去，直到问题规模足够小，很容易求出其解为止。
     将求出的小规模的问题的解合并为一个更大规模的问题的解，自底向上逐步求出原来问题的解。

【程序1】一个简单例子

        在一个整数组a[1...n]中，同时寻找最大值和最小值

【方法一】顺序扫描法
	min=a[1];
	max=a[1];
	扫描数组，对i从2到n做：
	   如果a[i]max，则max = a[i];
	返回max,min的值

【方法二】分治法
   基本思想： 
	（1）划分：将数组分割成两半
	（2）治理：在每一半中找到最大值和最小值。
	（3）合并：返回两个最大值中的最大值和两个最小值中的最小值。

minmax(int left, int right){
	if (right-left=1)  //如果只有两个元素直接解决
	   if (a[left]<a[right])  return(a[left], a[right]);
	      else return(a[right],a[left]);
	else  //否则递归解决
	   mid=(left+right)/2;   //将区间一分为二
	   (x1,y1)=minmax(left,mid);   //取左半边的最大最小值
	   (x2,y2)=minmax(mid+1,right);   //取右半边的最大最小值
	   x=min{x1,x2};   //求整体的最大最小值 
	   y=max{y1,y2}; 
	   return(x,y);   //返回最大最小值 
}

         以上算法要求函数同时返回两个值，显然是不符合C++/pascal语言语法的，请给出你的解决方案。
     C++/pascal中函数参数的传递是传值传递，如何进行传址传递？

【程序2】利用分治法求a的n次方

             分治的方法求an
【分析】
如果 n 是偶数，可以分为 (an/2)*(an/2)　　　　算法复杂度基本降低一半
如果 n 是奇数，可以分为 (an/2)*(an/2)*a　　　算法复杂度也基本降低一半
如果 n == 1 ，则直接返回 a

C++ code：
#include<iostream>
#include<cmath>
using namespace std;
int calc(int k,int n)
{
    if(n==1) return k;
    if(n%2==0) return pow(calc(k,n/2),2);
    return pow(calc(k,(n-1)/2),2)*k;
}
int main(){
    int a,n;
    cin >> a >> n;
    a=calc(a,n);
    cout << a << endl; 
} 

【程序3】二分查找

        给定n个从小到大排列的整数，查找其中是否存在x，若存在；返回位置，否则返回0。
样例输入：
5
12 5 6 87 20
87
样例输出：
4

int binarySerach(int left,int right){
	while(left <= right){
		int mid = (left + right) / 2;
		if(a[mid] == x) return mid;
		if(x > a[mid]) left = mid + 1;
		else  right = mid - 1;
    }
  return -1;
}

【程序4】归并排序

        对a[1...n]排序。
样例输入：
5
12 5 6 87 20
样例输出：
5 6 12 20 87

【分析】我们先看一个简单的问题：
    合并两个已排序的表
    将两个已排序的顺序表合并成一个有序表。顺序比较两者的相应元素，小者移入另一表中，反复如此，直至其中任一表都移入另一表为止。
如下图所示：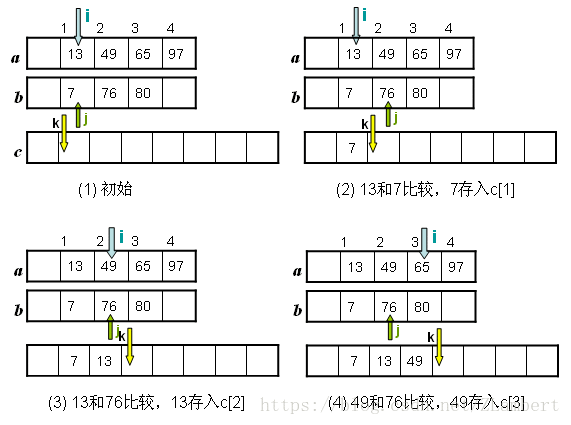

    后面的比较过程采用相同的方法，就不一一列举。

归并排序的过程(分治策略):
 （1）划分：将a[1...n]分为a[1...n/2] 和 a[n/2+1...n]两部分；
 （2）治理：分别对a[1...n/2] 和a[n/2+1...n]排序
 （3）组合：将两个有序子序列合并为一个有序序列 

 

归并排序C++模板：
#include<iostream>
using namespace std;
int a[5000],b[5000];
void merge(int l1,int r1,int l2,int r2){
	int t,i=l1,j=l2,k=l1;    //i,j分别为两段要合并的起始指针
	while(i<=r1 && j<=r2){   //将a[l1..r1]和a[l2..r2]合并到数组b对应位置
		if(a[i]<=a[j]){
			b[k]=a[i];
			i++;
		}else{
			b[k]=a[j];
			j++;
		}
		k++;
	}
	for(t=i;t<=r1;t++){b[k]=a[t];k++;}
	for(t=j;t<=r2;t++){b[k]=a[t];k++;}
	for(t=l1;t<=r2;t++) a[t]=b[t];    //再把合并后的数组赋给a
}
void mergesort(int left,int right){
	if(left<right){
		int mid=(left+right)/2;
		mergesort(left,mid);
		mergesort(mid+1,right);
		merge(left,mid,mid+1,right);
	}
}
int main(){
	int i,n;
	cin >> n;
	for (i=1;i<=n;i++) cin >> a[i];
	mergesort(1,n);
	for (i=1;i<=n;i++) cout << a[i] << ' ';
}