大整数运算详解-优快云博客

大整数运算

有时，我们碰到的整数超过了我们所熟知的整数类型int/integer，long/longint，以及long long/qword的范围，比如100位的整数，甚至更大。这时我们可以用字符串表示这些整数，但是字符串不能直接参与运算。在进行加减乘除运算前，将它们存储到数组中，并把字符转化成数字。

第1部分大整数的读入与存储

大整数的读入(字符串读入)
        C++:      或   pascal：
	string s;      var s:string;
	cin >> s;      readln(s);

大整数存储进数组中
如下图，我们把字符串反向存入数组中：
 

C++代码如下：
    for(int i=s.size()-1;i>=0;i--) a[s.size()-i]=int(s[i])-48;  //48可改为int('0')

第2部分大整数加法

        输入两个整数x,y(0<=x,y<=10200)，输出它们的和。
        加法关键在于进位，进位的时候，当前位模10，前一位加1。
        t = a[i]+b[i];
        c[i] = t mod 10; //mod在C++中为%
        c[i+1] = c[i+1] + t div 10; //div在C++中为/

C++ code:
#include<iostream>
#include<cstring>
using namespace std;
void sav(int a[300],string s){
	for(int i=s.size()-1;i>=0;i--) a[s.size()-i]=int(s[i])-48;
}  
void add(int a[],int b[],int la,int lb){
    int c[300],i=1;
    memset(c,0,sizeof(c));
    while(i<=la || i<=lb){
		int t = a[i] + b[i];
		c[i] += t % 10;
		c[i+1] += t / 10;
		i++;
    }
    while (c[i]==0 && i>1) i--;
    for (int j=i;j>=1;j--) cout << c[j];
    cout << endl;
}
int main(){
	int la,lb,a[301],b[301];
	string s1,s2;
	memset(a,0,sizeof(a));
	memset(b,0,sizeof(b));
	cin >> s1 >> s2;
	la=s1.size();lb=s2.size();
	sav(a,s1);
	sav(b,s2);
    add(a,b,la,lb);
    return 0;
}

第3部分大整数减法

        输入两个整数x,y(0<=x,y<=10200)，输出它们的差。
        减法关键在于借位，借位的时候，当前位加10，前一位减1。
        a[i] += 10;
        a[i+1] --;

C++ code:
#include<iostream>
#include<cstring>
using namespace std;
void sav(int a[300],string s){
	for(int i=s.size()-1;i>=0;i--) a[s.size()-i]=int(s[i])-48;
}  
void sub(int a[],int b[],int la,int lb){
    int c[300],i=1;
    memset(c,0,sizeof(c));
    while(i<=la){
		if(a[i]<b[i]){a[i]+=10;a[i+1]--;}
		c[i]=a[i]-b[i];
		i++;
    }
    while (c[i]==0 && i>1) i--;
    for (int j=i;j>=1;j--) cout << c[j];
    cout << endl;
}
int main(){
	int la,lb,a[301],b[301];
	string s,s1,s2;
	memset(a,0,sizeof(a));
	memset(b,0,sizeof(b));
	cin >> s1 >> s2;
	if((s1.size()<s2.size()) || (s1.size()==s2.size() && s1<s2)){
		cout << '-';
		s=s1;s1=s2;s2=s;
	}
	la=s1.size();lb=s2.size();
	sav(a,s1);
	sav(b,s2);
    sub(a,b,la,lb);
    return 0;
}

第4部分大整数乘法

输入两个整数x,y(0<=x,y<=10200)，输出它们的积。
如下图所示：

C++ code:
#include<iostream>
#include<cstring>
using namespace std;
void sav(int a[401],string s){
	for(int i=s.size()-1;i>=0;i--) a[s.size()-i]=int(s[i])-48;
}  
void mul(int a[],int b[],int la,int lb){
    int c[401],i,j;
    memset(c,0,sizeof(c));
    for(i=1;i<=la;i++)
      for(j=1;j<=lb;j++){
			int t=c[i+j-1]+a[i]*b[j];
			c[i+j-1]=(t%10);
			c[i+j]+=(t/10);
      }
    i=400;
    while (c[i]==0 && i>1) i--;
    for (int j=i;j>=1;j--) cout << c[j];
    cout << endl;
}
int main(){
	int la,lb,a[301],b[301];
	string s,s1,s2;
	memset(a,0,sizeof(a));
	memset(b,0,sizeof(b));
	cin >> s1 >> s2;
	la=s1.size();lb=s2.size();
    sav(a,s1);
	sav(b,s2);
    mul(a,b,la,lb);
    return 0;
}

第5部分大整数除法(高精度除以单精度)

输入两个整数x,y(0<=x<=10200,y在整数范围内)，输出它们的商和小数(保留2位小数)。
高精度除法是从高位向低位运算的，因此要用到反向存储，正序输出。
如下图所示（13587÷11）：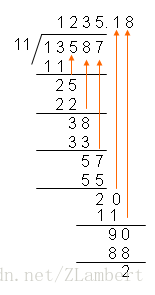

被除数使用字符串读入后，可以不存入数组中，直接从被除数的第1位依次取即可。


C++ code:
#include<iostream>
#include<cstring>
using namespace std;
void division(string s,int k,int w){   //w为小数位数
    int t=0,j=0;
    while(t<k){    //找出商的最高位对应s中的位置
	t=t*10+int(s[j])-48; 
	j++;
    }
    cout << t/k; t=t%k; 
    for(int i=j;i<s.size();i++){   //整数部分
		t=t*10+int(s[i])-48;
		if(t<k){
			cout << 0;
			continue;
		}
		cout << t/k;
		t=t%k;
    }
    cout << '.';    
    for(int i=0;i<w;i++){   //小数部分
		t*=10;
		cout << t/k;
		t=t%k;
    }
    cout << endl;
}
int main(){
	int k;
	string s;
	cin >> s >> k;
    division(s,k,2);
    return 0;
}

第6部分大整数阶乘

输入一个整数n(0<=n<=10200)，输出它的阶乘(n!)。
n! = 1 * 2 * 3 * ... * n
如下图所示：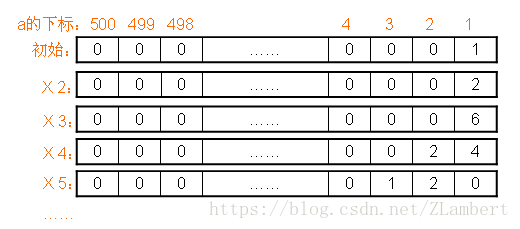

初始，a[1]赋值为1，其余位赋值位0；
对于 k = 2 -> n ：k乘以a[i]的每一位，超过10的就进位。

C++ code:
#include<iostream>
#include<cstring>
using namespace std;
int main(){
	int i,k,n,a[501];
	cin >> n;
	memset(a,0,sizeof(a));
	a[1]=1;
	for(k=2;k<=n;k++){
		for(i=1;i<500;i++) a[i]*=k;    //k乘数组每一位
		for(i=1;i<500;i++){    //进位
			a[i+1]+=a[i]/10;
			a[i]%=10;
		}
	}
	k=500;
	while(a[k]==0)k--;    //寻找最高位是哪一位
	for(i=k;i>=1;i--) cout << a[i];   //输出阶乘
	cout << endl;
    return 0;
}

第7部分压位优化

我们前面把字符串存入数组中都是把字符串的每一位存入数组每一位，这样浪费了空间和时间。比如2个数都是1000位，他们相乘就是1000*1000次循环，可能超时。
我们可以尝试着把字符串分成4位一段，转成数值存在数组a中；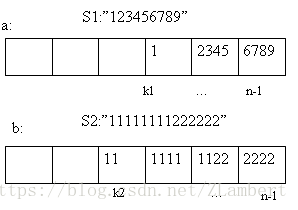

1、字符串转成数值存入数值中(4位一存)


C++ code:
	string s;
	cin >> s;
	i=s.size()-4;
	while(i>=0){
		k++;
		t=(int(s[i])-48)*1000 + (int(s[i+1])-48)*100 + (int(s[i+2])-48)*10
		  + int(s[i+3])-48;
		a[k]=t;
		i-=4;
	}
	t=0;
	if(i<0){
		for(int j=0;j<=i+3;j++) t=t*10+int(s[j])-48;
		a[k+1]=t;
	}

2、加减乘除的运算

加减乘除的运算和前面的完全一样。唯一区别的是，因为每个数组元素存储的都是4位数，运算时把10给成10000。
如加法：
        t = a[i]+b[i];
        c[i] = t mod 10000;
        c[i+1] = c[i+1] + t / 10000;

3、结果的输出

压位输出时，除最高位外，因为每位存储的都是4位。如果当前a[i]存储的不足4位，那么前面加上0不足4位。


C++ code:
	for(i=k;i>=1;i--)
	  if(a[i]>=1000) cout << a[i];
	     else if(a[i]>=100) cout << "0" << a[i];
	        else if(a[i]>=10) cout << "00" << a[i];
	           else cout << "000" << a[i];