一.公式介绍
卷积分为离散卷积和连续卷积,它们的区别就是连续和离散的区别,这里以离散卷积举例。
S(n)=(f∗g)(f*g)(f∗g)[n]= ∑m=0N−1f(m)g(n−m)\sum_{m=0}^{N-1} {f(m)g(n-m)}{}∑m=0N−1f(m)g(n−m)
S(n)为卷积结果序列,长度为len(f(m)f(m)f(m))+len(g(m)g(m)g(m))-1. N为信号f(m)f(m)f(m)的长度,f(m),g(m)f(m),g(m)f(m),g(m)为离散信号。这里举个例子:f(m)=[1 2 3 4]和g(m)=[2 3 1]f(m)=[1 \ 2 \ 3 \ 4]和g(m)=[2 \ 3 \ 1]f(m)=[1 2 3 4]和g(m)=[2 3 1]
二.计算一维卷积
1.理解公式里面的数据。
将f(m)f(m)f(m)序列从小到大排列(F0,F1,F2,F3F_0,F_1,F_2,F_3F0,F1,F2,F3)。因为上述公式中f(m)f(m)f(m)里面的m的序列是从小到大,(其中,F0=1F_0=1F0=1,F1=2F_1=2F1=2,F2=3F_2=3F2=3,F3=4F_3=4F3=4,其他值均为0)。而g(m)g(m)g(m)序列从大到小排列,因为G的序列是-m,(其中,G0=2G_0=2G0=2,G1=3G_1=3G1=3,G2=1G_2=1G2=1,其他值均为0),然后再将两个序列开头对齐。
2.逐个计算S(n)
注:f(m)f(m)f(m)的图像是f(m)f(m)f(m)对y轴的反转,g(−m)g(-m)g(−m)就是g(m)g(m)g(m)的序列反转,g(n−m)g(n-m)g(n−m)的意义是把g(−m)g(-m)g(−m)平移n点,n为正,向X轴右侧平移,n为负,向X轴右侧左移。
1>S(0)的计算中,f(m)f(m)f(m)和g(n−m)g(n-m)g(n−m)的图
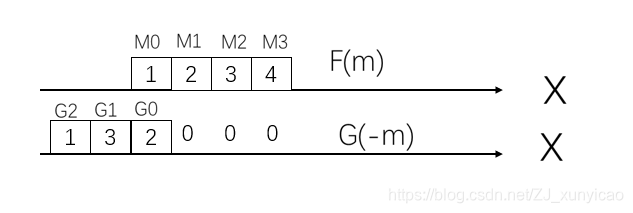
S(0)=f(0)f(0)f(0).g(0−0)g(0-0)g(0−0)+f(1)f(1)f(1).g(0−1)g(0-1)g(0−1)+f(2)f(2)f(2).g(0−2)g(0-2)g(0−2)+f(3)f(3)f(3).g(0−3)g(0-3)g(0−3)
=1 ×\times× 2+2 ×\times× 0+3 ×\times× 0+4 ×\times× 0=2
2>S(1)的计算中,f(m)f(m)f(m)和g(n−m)g(n-m)g(n−m)的图
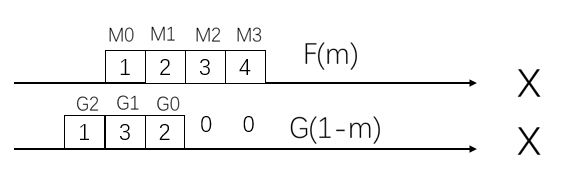
S(1)=f(0)f(0)f(0).g(1−0)g(1-0)g(1−0)+f(1)f(1)f(1).g(1−1)g(1-1)g(1−1)+f(2)f(2)f(2).g(1−2)g(1-2)g(1−2)+f(3)f(3)f(3).g(1−3)g(1-3)g(1−3)
=1 ×\times× 3+2 ×\times× 2+3 ×\times× 0+4 ×\times× 0=7
3>S(2)的计算中,f(m)f(m)f(m)和g(n−m)g(n-m)g(n−m)的图
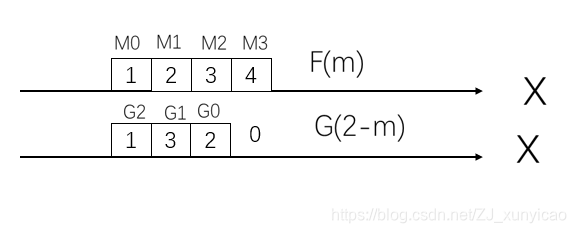
S(2)=f(0)f(0)f(0).g(2−0)g(2-0)g(2−0)+f(1)f(1)f(1).g(2−1)g(2-1)g(2−1)+f(2)f(2)f(2).g(2−2)g(2-2)g(2−2)+f(3)f(3)f(3).g(2−3)g(2-3)g(2−3)
=1 ×\times× 1+2 ×\times× 3+3 ×\times× 2+4 ×\times× 0=13
4>S(3)的计算中,f(m)f(m)f(m)和g(n−m)g(n-m)g(n−m)的图
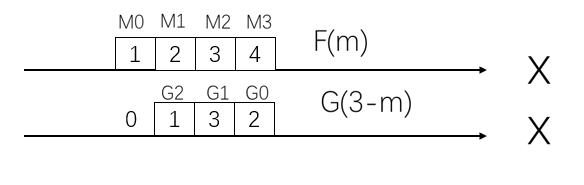
S(3)=f(0)f(0)f(0).g(3−0)g(3-0)g(3−0)+f(1)f(1)f(1).g(3−1)g(3-1)g(3−1)+f(2)f(2)f(2).g(3−2)g(3-2)g(3−2)+f(3)f(3)f(3).g(3−3)g(3-3)g(3−3)
=1 ×\times× 0+2 ×\times× 1+3 ×\times× 3+4 ×\times× 2=19
5>S(4)的计算中,f(m)f(m)f(m)和g(n−m)g(n-m)g(n−m)的图
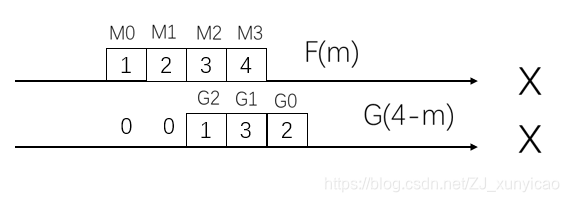
S(4)=f(0)f(0)f(0).g(4−0)g(4-0)g(4−0)+f(1)f(1)f(1).g(4−1)g(4-1)g(4−1)+f(2)f(2)f(2).g(4−2)g(4-2)g(4−2)+f(3)f(3)f(3).g(4−3)g(4-3)g(4−3)
=1 ×\times× 0+2 ×\times× 0+3 ×\times× 1+4 ×\times× 3=15
6>S(5)的计算中,f(m)f(m)f(m)和g(n−m)g(n-m)g(n−m)的图
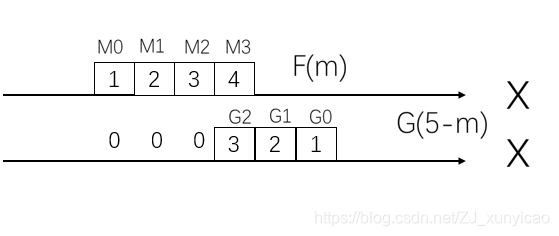
S(5)=f(0)f(0)f(0).g(5−0)g(5-0)g(5−0)+f(1)f(1)f(1).g(5−1)g(5-1)g(5−1)+f(2)f(2)f(2).g(5−2)g(5-2)g(5−2)+f(3)f(3)f(3).g(5−3)g(5-3)g(5−3)
=1 ×\times× 0+2 ×\times× 0+3 ×\times× 0+4 ×\times× 1=4
7>当g(−m)g(-m)g(−m)向右移了6个单位时,可以看到,F(X)和G(X)F(X)和G(X)F(X)和G(X)没有重叠的项,n=6也没有意义了。所以S(n)S(n)S(n)的最大长度要使得两个序列至少有1个项重合,即两个序列长度求和再减去重合的一项的长度。(开头介绍的结果序列长度公式)
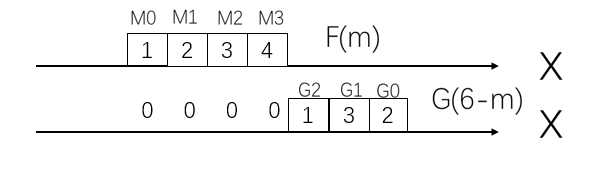
最终结果为:S(n)=[2 7 13 19 15 4]S(n)=[2 \ 7 \ 13 \ 19 \ 15 \ 4 ]S(n)=[2 7 13 19 15 4]
三.总结一下
在卷积运算时可以交换顺序,F(X)和G(X)F(X)和G(X)F(X)和G(X)的顺序和长度都不重要,一维卷积及是一个序列反转滑动卷积另一个序列。








 本文详细介绍了如何计算一维卷积,通过实例解析卷积公式S(n)的计算过程,展示f(m)和g(n-m)的图像,并探讨了序列长度的确定原则。最后,给出了具体的卷积结果序列。
本文详细介绍了如何计算一维卷积,通过实例解析卷积公式S(n)的计算过程,展示f(m)和g(n-m)的图像,并探讨了序列长度的确定原则。最后,给出了具体的卷积结果序列。
















 2308
2308

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








