非线性支持向量机及代码

1.问题引入

线性支持向量机模型假设其训练样本是线性可分的，即存在一个超平面将两个类完全分开。然而在现实任务中，或许样本空间根本就不存在一个超平面能进行分类。下图是不存在分类超平面的例子：

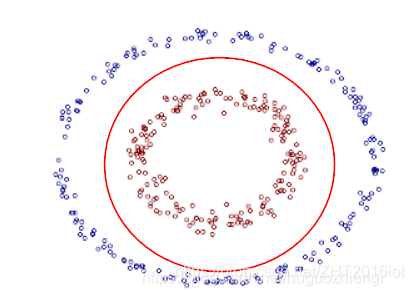
为了解决这个问题，可以将样本从原始空间映射到一个更高的特征空间，使得样本在高维的特征空间变得线性可分。映射到高维一定能线性可分吗？幸运地是，如果原始空间是有限的，则一定存在一个特征高维空间使得样本线性可分。

我们定义映射$\varphi (x)$将$x$从m维空间映射到n维空间(n>m),于是在特征空间的超平面表示为：
$$\begin{array}{r}f(x)=w^T\varphi (x)+b\end{array}$$
在特征空间的线性SVM模型为：
$$\begin{array}{rl}& mi{n}_{[w,b]}\frac{1}{2}||w|{|}^2\\ & \\ & s.t.y_i(w^T\varphi (x_i)+b)\ge 1,i\in [1,m]\end{array}$$
其对偶问题为：
$$\begin{array}{rl}& ma{x}_{[\alpha ]}\sum _{i=1}^m{\alpha }_i-\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j\varphi (x_i{)}^T\varphi (x_j)\\ & \\ & s.t.\sum _{i=1}^m{\alpha }_i{y}_i,{\alpha }_i\ge 0,i\in [1,m]\end{array}$$
从上述表达式中发现，样本向高维空间映射后，难度在于计算$\varphi (x_i{)}^T\varphi (x_j)$,因为特征空间可能维度很高，甚至是无穷维。故而，我们定义这样一个函数:
$$\begin{array}{r}k(x_i,x_j)=\varphi (x_i{)}^T\varphi (x_j)\end{array}$$
这就是核函数。引入核函数，我们可以避免高维空间的计算，也不用知道$\varphi (.)$的具体形式。

2. 核函数

核函数形式如下：
$$\begin{array}{r}k(x_i,x_j)=\varphi (x_i{)}^T\varphi (x_j)\end{array}$$
我们举个例子来说明核函数的强大：
$$\begin{array}{rl}令X=& (x_1,x_2{)}^T\\ Y=& (y_1,y_2{)}^T\\ \varphi (X)=& (x_1^2,\\ \varphi (Y)=& \\ & \\ k(X,Y)=& \\ =& \\ =& \\ =& \end{array}$$