基于ABAQUS金属轧制成型仿真分析

一、轧制成型基本原理

轧制过程涉及复杂的力学行为，主要包括：

1. 弹塑性变形：金属材料在轧辊压力作用下发生塑性流动，同时伴随弹性变形
2. 接触摩擦：轧辊与金属表面存在摩擦作用，影响变形区应力分布
3. 温度效应：热轧过程中温度场变化显著影响材料流动应力

---

二、ABAQUS仿真关键步骤

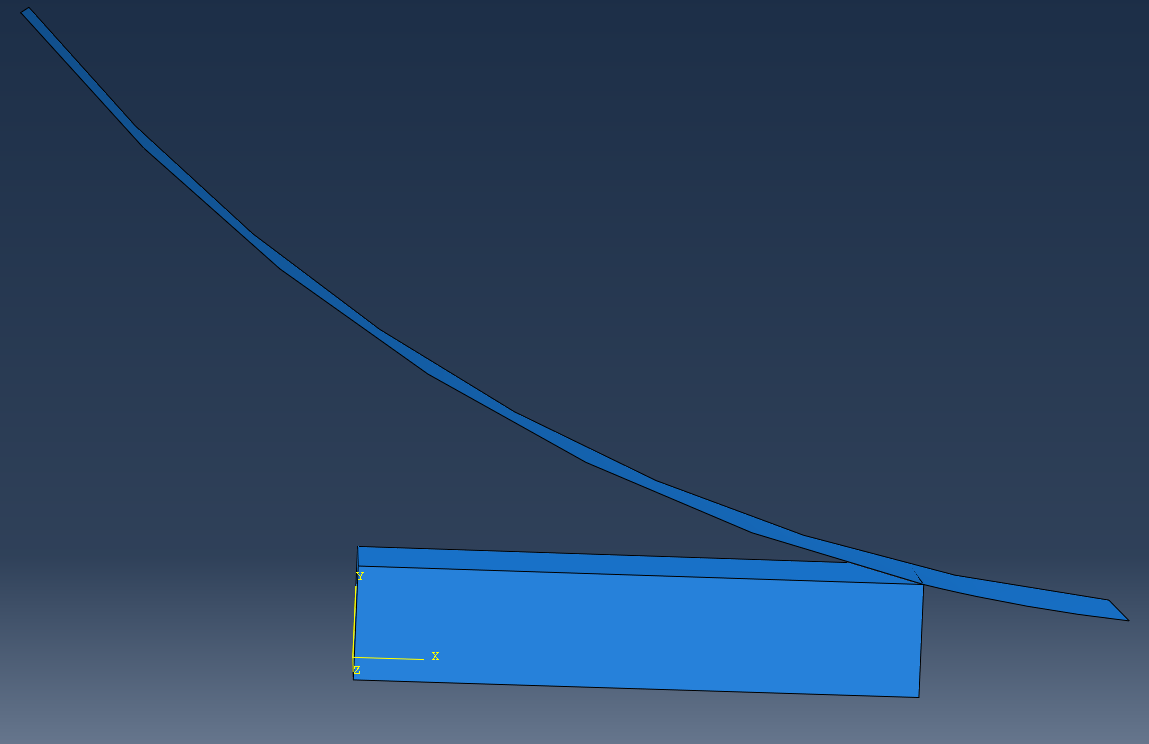
1. 几何建模

• 轧辊建模为解析刚体（Analytical Rigid）
• 轧件采用三维可变形体（3D Deformable）
• 典型几何参数：
  • 轧辊半径 R
  • 轧件初始厚度 h0
  • 压下量 ​编辑

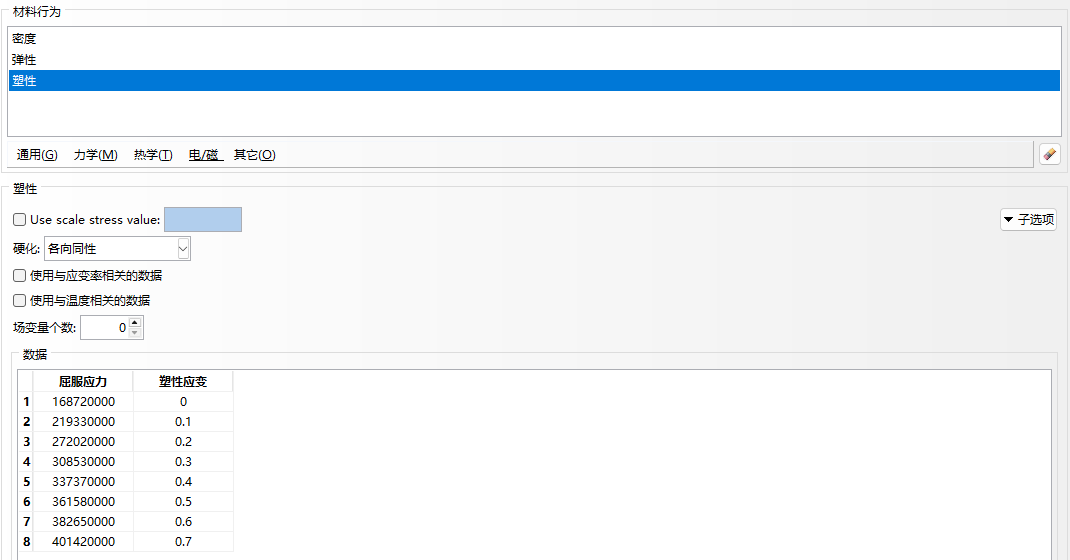
2. 材料定义

# 示例：定义弹塑性材料
material = mdb.models['Model-1'].Material(name='Steel')
material.Density(table=((7.85e-9, ), ))
material.Elastic(table=((15e5, 0.3), ))
material.Plastic(table=(
    (1.6878e8, 0.0), 
    (2.1933e8, 0.1), 
    (2.7202e8, 0.2),
    (3.0853e8, 0.3), 
    (3.3737e8, 0.4), 
    (3.6158e8, 0.5),
    (3.8265e8, 0.6), 
    (4.0142e8, 0.7), # 真实应力-塑性应变数据
))

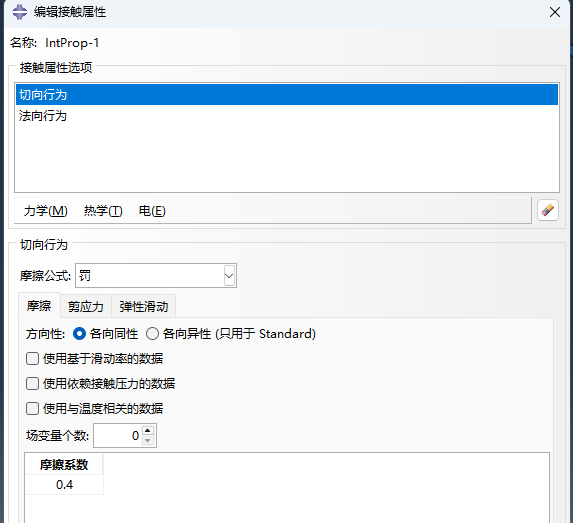
3. 接触设置

• 采用面面接触（Surface-to-Surface）
• 摩擦模型选择库伦摩擦：法向使用硬接触，切向接触为罚接触，摩擦系数设置为0.4。
• 
• 

4. 边界条件

• 轧辊：施加旋转速度 
• 轧件：端部施加牵引速度
• 

5. 网格划分

• 轧件采用结构化网格
• 轧制方向网格可加密：

  mesh.setElementType(elemType=C3D8R)  # 减缩积分单元
  mesh.setMeshingControls(elemShape=HEX, technique=SWEEP)
  

  

---

三、热力耦合分析（热轧工况）

对于热轧过程，后续可考虑加入温度场影响：

1. 材料温度相关性：

   material.Plastic(
       dependencies=2, 
       table=(
           (500, 0.0, 350e6),  # 温度, 应变, 应力
           (500, 0.1, 420e6),
           (1000, 0.0, 150e6)
       )
   )
   

---

四、结果后处理

通过 ABAQUS/Viewer 可分析：

1. 等效应力云图（Mises Stress）
2. 轧制力时程曲线

---

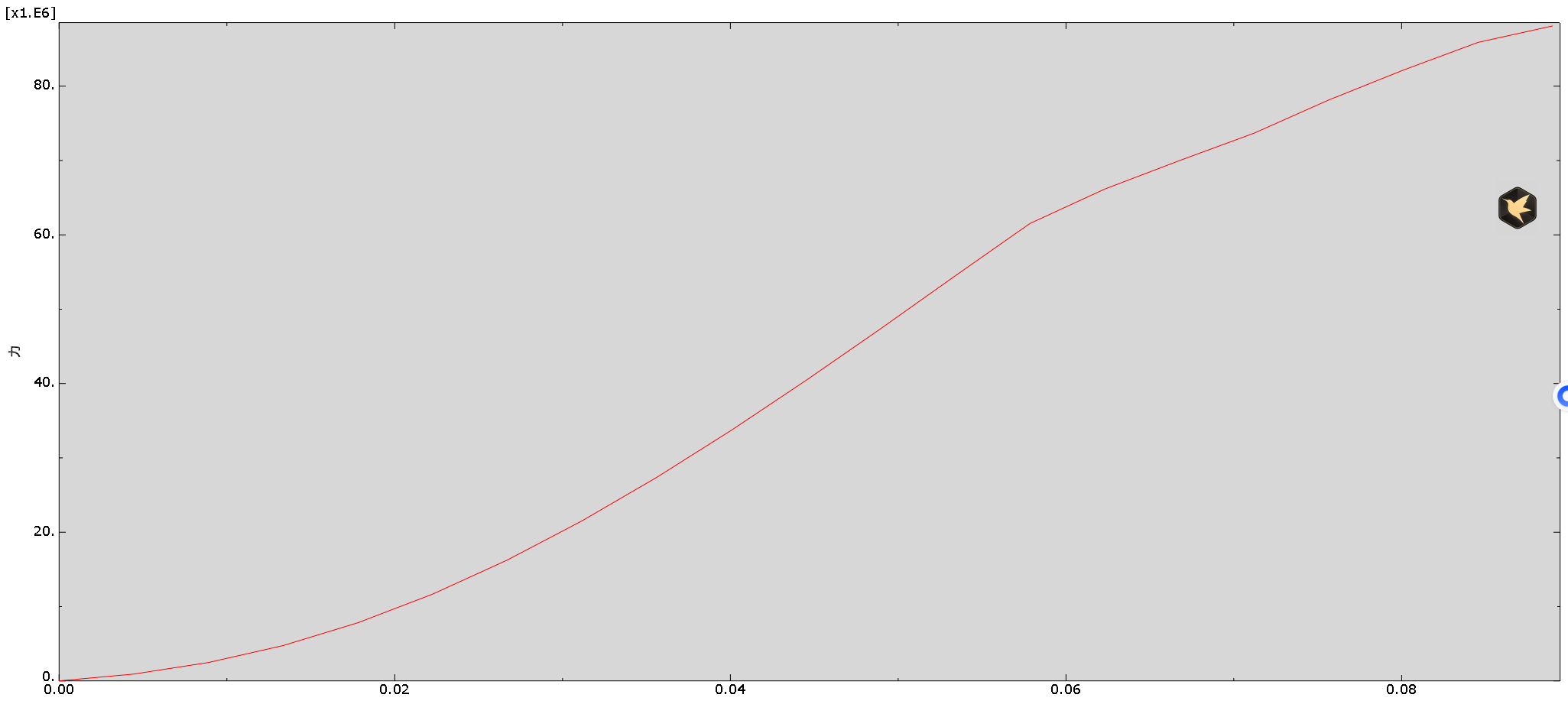
五、应用案例

某钢厂铝板热轧过程仿真：

参数	值
轧辊半径	350 mm
初始厚度	50 mm
终了厚度	25 mm
轧制温度	480 ℃
轧制力峰值	12.8 MN (仿真) vs 13.2 MN (实测)

---

六、常见问题对策

1. 收敛困难：

   • 减小初始增量步
   • 调整接触罚函数刚度

   contact.setTangentialBehavior(
       frictionCoeff=0.3, 
       penalty=0.1  # 降低罚数
   )
   

2. 网格畸变：

   • 采用自适应网格重划分（ALE）
   • 增加轧制方向单元数