最小路径和（动态规划）

题目：
给定一个包含非负整数的 m x n 网格 grid ，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

说明：每次只能向下或者向右移动一步。

示例 1：

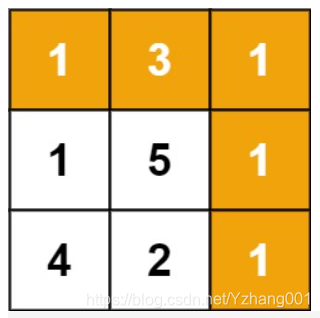
输入：grid = [[1,3,1],[1,5,1],[4,2,1]]
输出：7
解释：因为路径 1→3→1→1→1 的总和最小。
示例 2：

输入：grid = [[1,2,3],[4,5,6]]
输出：12

提示：

m == grid.length
n == grid[i].length
1 <= m, n <= 200
0 <= grid[i][j] <= 100

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/minimum-path-sum

1、确定状态：
根据最后一步，在网格中要么是grid[rows-1][cols]往下走，要么就是grid[rows][cols-1]往右走，只能是这两种情况，因为题目要求只能是往下和往右走。
2、状态方程，根据以上分析可以得出最小路径和的状态方程为：
mixv[i][j] = min(mixv[i-1][j]+grid[i][j],mixv[i][j-1]+grid[i][j])
3、边界条件应该考虑当j=0,即列为第0列时，只能向下走，即
minv[i][0] = (minv[i-1][0]+grid[i][0]);
同理，行i=0时有：
minv[0][j] = (minv[0][j-1]+grid[0][j]);
初始条件就是只有一格时，minv[0][0] = grid[0][0]
4、计算顺序：由于计算minv[i][j]时会用到miv[i-1][j]和miv[i][j-1],即要用到上边和左边的代价数组，所以我们从左往右，从上往下计算即可。
C语言代码如下：

int minPathSum(int** grid, int gridSize, int* gridColSize){
    int col = gridColSize[0];
    int minv[gridSize][col];
    minv[0][0] = grid[0][0];
    for(int i=1; i<gridSize; i++)
        minv[i][0] = (minv[i-1][0]+grid[i][0]);
    for(int j=1; j<col; j++)
        minv[0][j] = (minv[0][j-1]+grid[0][j]);
    for(int i=1; i<gridSize; i++)
    {
        for(int j=1; j<col; j++)
        {
            minv[i][j] = fmin(minv[i-1][j],minv[i][j-1])+grid[i][j];
        }
    }
    return minv[gridSize-1][col-1];
}

提交结果如下：