Matplotlib从入门到精通：LLM开发者的可视化实战指南

  【个人主页：玄同765】

大语言模型（LLM）开发工程师｜中国传媒大学·数字媒体技术（智能交互与游戏设计）

深耕领域：大语言模型开发 / RAG知识库 / AI Agent落地 / 模型微调

技术栈：Python / LangChain/RAG（Dify+Redis+Milvus）| SQL/NumPy | FastAPI+Docker ️

工程能力：专注模型工程化部署、知识库构建与优化，擅长全流程解决方案 

      

专栏传送门：LLM大模型开发 项目实战指南、Python 从真零基础到纯文本 LLM 全栈实战、​​​​​从零学 SQL + 大模型应用落地、大模型开发小白专属：从 0 入门 Linux&Shell

     

「让AI交互更智能，让技术落地更高效」

欢迎技术探讨/项目合作！ 关注我，解锁大模型与智能交互的无限可能

数据可视化的基石：Matplotlib的核心价值与应用场景

在数据驱动决策的时代，可视化已成为连接原始数据与人类认知的重要桥梁。Matplotlib作为Python生态中历史最悠久、应用最广泛的可视化库，自2003年首次发布以来，已发展成为科研、工程、商业分析等领域不可或缺的基础工具。其核心价值在于提供了一套完整的底层绘图API，支持从简单折线图到复杂3D曲面的全场景可视化需求，同时保持了高度的可定制性和跨平台兼容性。

在实际应用中，Matplotlib展现出强大的场景适应性：在学术研究中，它能生成符合期刊要求的 publication-ready 图表；在工业界，数据科学家用它快速探索数据分布特征；而在LLM开发领域，Matplotlib更是扮演着关键角色，从训练过程中的损失曲线监控，到模型推理结果的对比分析，再到大规模文本数据的特征可视化，都离不开其灵活的图表绘制能力。

与新兴的可视化工具相比，Matplotlib的独特优势在于：

• 完全可控的绘图逻辑：从坐标轴刻度到字体样式，每个细节均可精确调整

• 丰富的图表类型支持：覆盖2D/3D超过30种基础图表类型

• 强大的扩展生态：作为Seaborn、Pandas可视化接口等高级工具的底层引擎

• 稳定的版本兼容性：Matplotlib 3.x系列已形成成熟的API体系，向下兼容性良好

环境配置与基础概念

安装与环境验证

Matplotlib的安装过程简洁高效，支持多种安装方式以适应不同开发环境需求。对于大多数用户，推荐使用pip或conda包管理器进行安装，这两种方式均能自动处理依赖关系，确保库文件的完整性。

# 使用pip安装最新稳定版
pip install matplotlib==3.8.2

# 使用conda安装（推荐科学计算环境）
conda install matplotlib=3.8.2

安装完成后，可通过以下代码验证环境是否配置正确：

import matplotlib
import matplotlib.pyplot as plt
import numpy as np

# 打印版本信息
print(f"Matplotlib版本: {matplotlib.__version__}")  # 应输出3.8.2或兼容版本

# 创建简单图表验证渲染功能
fig, ax = plt.subplots(figsize=(6, 4))
x = np.linspace(0, 2*np.pi, 100)
ax.plot(x, np.sin(x))
ax.set_title("环境验证：正弦曲线绘制")
plt.savefig("environment_verification.png", dpi=300, bbox_inches="tight")
plt.close()

若代码运行无错误且成功生成PNG图像文件，表明Matplotlib环境已正确配置。对于使用Jupyter Notebook的用户，建议通过%matplotlib inline魔法命令启用交互式图表显示，或使用%matplotlib notebook获得更多交互功能。

核心概念与绘图流程

Matplotlib采用面向对象的设计思想，其核心架构包含几个关键组件，理解这些组件的关系是掌握Matplotlib的基础：

核心组件	作用描述	常用操作
Figure	图表容器，可包含多个Axes对象	fig = plt.figure(figsize=(10, 6))
Axes	绘图区域，一个Figure可包含多个子图(Axes)	ax = fig.add_subplot(111) 或 fig, ax = plt.subplots()
Axis	坐标轴，每个Axes包含x轴和y轴	ax.set_xlim(0, 10); ax.set_xticks([1,3,5])
Artist	所有可见元素的基类，包括文本、线条、标记等	line, = ax.plot(x, y, 'r-', linewidth=2)

Matplotlib的标准绘图流程遵循"创建容器→绘制数据→美化修饰→输出展示"的四步模型：

# 1. 创建图表容器
fig, ax = plt.subplots(figsize=(8, 5))  # 同时创建Figure和Axes对象

# 2. 绘制基础数据
x = np.arange(0, 10, 0.1)
y = np.sin(x)
line, = ax.plot(x, y, label='sin(x)')  # plot返回Line2D对象，便于后续修改

# 3. 美化与修饰
ax.set_title('正弦函数曲线', fontsize=14, pad=20)  # 设置标题及字体大小
ax.set_xlabel('X轴', fontsize=12, labelpad=10)    # 设置X轴标签
ax.set_ylabel('Y轴', fontsize=12, labelpad=10)    # 设置Y轴标签
ax.grid(True, linestyle='--', alpha=0.7)          # 添加网格线
ax.legend(loc='upper right')                      # 显示图例

# 4. 输出与展示
plt.tight_layout()  # 自动调整布局，避免元素重叠
plt.savefig('basic_plotting_flow.png', dpi=300, bbox_inches='tight')  # 保存为PNG图片
plt.show()  # 在交互环境中显示图表

这种基于对象的绘图模式虽然比pyplot的状态机接口稍显繁琐，但带来了更精确的控制能力和更清晰的代码结构，特别适合构建复杂图表或在大型项目中使用。

基础图表绘制实战

折线图：趋势可视化的利器

折线图是展示数据随连续变量变化趋势的最常用图表类型，在模型训练监控、时间序列分析等场景中应用广泛。Matplotlib的plot方法提供了丰富的参数控制线条样式、标记形状和颜色配置，能够满足不同场景下的可视化需求。

以下代码展示了如何创建一个包含多条曲线、自定义样式的折线图，并添加误差线以展示数据不确定性：

import numpy as np
import matplotlib.pyplot as plt

# 设置中文字体，确保中文正常显示
plt.rcParams["font.family"] = ["SimHei", "WenQuanYi Micro Hei", "Heiti TC"]
plt.rcParams['axes.unicode_minus'] = False  # 解决负号显示问题

# 生成示例数据
x = np.linspace(0, 10, 50)
y1 = np.sin(x)
y2 = np.cos(x)
y3 = np.sin(x) * np.cos(x)

# 添加随机噪声模拟真实数据
np.random.seed(42)  # 设置随机种子，确保结果可复现
y1_noise = y1 + np.random.normal(0, 0.1, size=len(x))
y2_noise = y2 + np.random.normal(0, 0.1, size=len(x))
y3_noise = y3 + np.random.normal(0, 0.1, size=len(x))

# 创建图表和坐标轴
fig, ax = plt.subplots(figsize=(10, 6))

# 绘制带误差线的折线图
ax.errorbar(x, y1_noise, yerr=0.1, fmt='-o', color='#1f77b4',
            ecolor='lightgray', elinewidth=2, capsize=4,
            label='正弦曲线', alpha=0.8)

ax.errorbar(x, y2_noise, yerr=0.1, fmt='-s', color='#ff7f0e',
            ecolor='lightgray', elinewidth=2, capsize=4,
            label='余弦曲线', alpha=0.8)

# 绘制平滑曲线（无标记点）
ax.plot(x, y3, '-', color='#2ca02c', linewidth=2, label='乘积曲线')

# 自定义坐标轴和标题
ax.set_title('三角函数曲线对比', fontsize=16, pad=20)
ax.set_xlabel('X值', fontsize=14, labelpad=10)
ax.set_ylabel('函数值', fontsize=14, labelpad=10)
ax.set_xlim(0, 10)  # 设置X轴范围
ax.set_ylim(-1.5, 1.5)  # 设置Y轴范围

# 添加网格线和图例
ax.grid(True, linestyle='--', alpha=0.6)
ax.legend(fontsize=12, loc='lower center', ncol=3)

# 添加注释文本
ax.annotate('sin(x)最大值', xy=(np.pi/2, 1), xytext=(np.pi/2 + 0.5, 1.2),
            arrowprops=dict(facecolor='black', shrink=0.05, width=1),
            fontsize=12, fontweight='bold')

# 调整布局并保存
plt.tight_layout()
plt.savefig('line_chart_demo.png', dpi=300, bbox_inches='tight')
plt.show()

折线图绘制中常用的格式化参数可通过fmt参数快捷设置，其格式为[marker][line][color]，例如'o--r'表示圆形标记、虚线、红色线条。下表列出了常用的格式化选项：

参数类型	常用选项	说明
标记(marker)	'o', 's', '^', 'D', '*'	数据点标记形状
线条(line)	'-', '--', '-.', ':'	线条样式
颜色(color)	'r', 'g', 'b', 'y', 'k'	颜色简称
颜色(color)	'#FF5733', '#2ECC71'	十六进制颜色码
透明度(alpha)	0.1~1.0	数值越小越透明

柱状图与直方图：数据分布的直观呈现

柱状图和直方图是展示分类数据和连续数据分布的重要工具，在LLM开发中常用于比较不同模型性能指标、分析文本长度分布等场景。虽然两者视觉形式相似，但应用场景有本质区别：柱状图适用于比较离散类别数据，而直方图用于展示连续数据的分布特征。

以下代码实现了一个包含多组数据的簇状柱状图和一个叠加式直方图的组合展示：

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.patches as mpatches

# 设置中文字体
plt.rcParams["font.family"] = ["SimHei", "WenQuanYi Micro Hei", "Heiti TC"]
plt.rcParams['axes.unicode_minus'] = False

# 生成柱状图数据
categories = ['模型A', '模型B', '模型C', '模型D']
precision = [0.82, 0.85, 0.78, 0.90]
recall = [0.78, 0.81, 0.84, 0.87]
f1_score = [0.80, 0.83, 0.81, 0.88]

# 设置柱状图位置
x = np.arange(len(categories))  # 分类标签位置
width = 0.25  # 柱状图宽度

# 生成直方图数据（模拟文本长度分布）
np.random.seed(42)
text_lengths_base = np.random.normal(500, 100, 1000)  # 基础模型文本长度
text_lengths_finetuned = np.random.normal(650, 120, 1000)  # 微调后模型文本长度

# 创建2x1的子图布局
fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(12, 10), height_ratios=[1, 1])

# 绘制簇状柱状图（模型性能对比）
rects1 = ax1.bar(x - width, precision, width, label='精确率', color='#1f77b4', alpha=0.8)
rects2 = ax1.bar(x, recall, width, label='召回率', color='#ff7f0e', alpha=0.8)
rects3 = ax1.bar(x + width, f1_score, width, label='F1分数', color='#2ca02c', alpha=0.8)

# 设置柱状图标题和坐标轴
ax1.set_title('不同模型性能指标对比', fontsize=15, pad=20)
ax1.set_xticks(x)
ax1.set_xticklabels(categories, fontsize=12)
ax1.set_ylabel('分数', fontsize=14, labelpad=10)
ax1.set_ylim(0.7, 0.95)  # 设置Y轴范围，突出差异

# 添加数据标签
def add_labels(rects, ax):
    for rect in rects:
        height = rect.get_height()
        ax.annotate(f'{height:.2f}',
                    xy=(rect.get_x() + rect.get_width() / 2, height),
                    xytext=(0, 3),  # 3 points vertical offset
                    textcoords="offset points",
                    ha='center', va='bottom', fontsize=11)

add_labels(rects1, ax1)
add_labels(rects2, ax1)
add_labels(rects3, ax1)

# 添加网格线和图例
ax1.grid(axis='y', linestyle='--', alpha=0.6)
ax1.legend(fontsize=12, loc='upper center', ncol=3)

# 绘制叠加直方图（文本长度分布）
ax2.hist(text_lengths_base, bins=30, alpha=0.6, label='基础模型',
         color='#1f77b4', edgecolor='white', density=True)
ax2.hist(text_lengths_finetuned, bins=30, alpha=0.6, label='微调后模型',
         color='#ff7f0e', edgecolor='white', density=True)

# 设置直方图标题和坐标轴
ax2.set_title('文本生成长度分布对比', fontsize=15, pad=20)
ax2.set_xlabel('文本长度（字符数）', fontsize=14, labelpad=10)
ax2.set_ylabel('概率密度', fontsize=14, labelpad=10)
ax2.set_xlim(0, 1000)

# 添加垂直参考线（均值）
mean_base = np.mean(text_lengths_base)
mean_finetuned = np.mean(text_lengths_finetuned)
ax2.axvline(mean_base, color='#1f77b4', linestyle='--', linewidth=2,
            label=f'基础模型均值: {mean_base:.1f}')
ax2.axvline(mean_finetuned, color='#ff7f0e', linestyle='--', linewidth=2,
            label=f'微调后均值: {mean_finetuned:.1f}')

# 添加网格线和图例
ax2.grid(axis='y', linestyle='--', alpha=0.6)
ax2.legend(fontsize=12)

# 调整布局并保存
plt.tight_layout(pad=4.0)
plt.savefig('bar_histogram_demo.png', dpi=300, bbox_inches='tight')
plt.show()

柱状图的关键参数配置决定了其视觉效果和信息传递效率：

参数	作用	推荐设置
width	柱子宽度	0.20.3（多组数据），0.60.8（单组数据）
alpha	透明度	0.7~0.9（叠加显示时）
edgecolor	边框颜色	'white'（增强分离感）
ylim	Y轴范围	从略低于最小值开始，为数据标签留出空间

对于直方图，bin的选择直接影响分布形态的呈现：

• 数据量较少时（<100），推荐bin数量=数据量的平方根

• 数据量中等时（100~1000），可使用Freedman-Diaconis规则自动计算

• 数据量较大时（>1000），可通过bins='auto'让Matplotlib自动优化

散点图与热力图：关系与相关性分析

散点图和热力图是探索变量间关系的强大工具，在LLM开发中常用于特征相关性分析、嵌入空间可视化、注意力权重分布展示等场景。散点图通过二维平面上的点分布直观展示两个变量间的关系，而热力图则通过颜色编码展示矩阵数据的数值大小，特别适合呈现高维数据的密度分布或相关系数矩阵。

以下代码实现了一个综合散点图分析和特征相关性热力图的可视化方案：

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA

# 设置中文字体
plt.rcParams["font.family"] = ["SimHei", "WenQuanYi Micro Hei", "Heiti TC"]
plt.rcParams['axes.unicode_minus'] = False

# 生成模拟数据（模拟LLM特征空间）
np.random.seed(42)
X, y = make_classification(
    n_samples=500, n_features=10, n_informative=5, n_redundant=2,
    n_clusters_per_class=2, random_state=42
)

# 标准化特征
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

# 计算相关系数矩阵
corr_matrix = np.corrcoef(X_scaled.T)

# 使用PCA降维用于散点图可视化
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X_scaled)

# 生成第三维度数据（模拟模型置信度）
confidence = np.abs(np.random.normal(0.5, 0.2, size=len(X)))
confidence = np.clip(confidence, 0, 1)  # 确保置信度在0-1范围内

# 创建2x1的子图布局
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(14, 6))

# 绘制气泡散点图（PCA降维特征空间）
scatter = ax1.scatter(
    X_pca[:, 0], X_pca[:, 1],
    c=y,  # 使用类别作为颜色
    s=confidence * 200 + 50,  # 使用置信度作为点大小
    cmap='viridis',
    alpha=0.7,
    edgecolors='w',
    linewidth=0.5
)

# 设置散点图标题和坐标轴
ax1.set_title('LLM特征空间PCA降维可视化', fontsize=15, pad=20)
ax1.set_xlabel('主成分1', fontsize=13, labelpad=10)
ax1.set_ylabel('主成分2', fontsize=13, labelpad=10)
ax1.grid(True, linestyle='--', alpha=0.6)

# 添加颜色条和图例
cbar = plt.colorbar(scatter, ax=ax1)
cbar.set_label('类别', rotation=270, labelpad=20)

# 创建大小图例（置信度）
sizes = [0.2, 0.5, 0.8]
legend_elements = [
    mpatches.Circle((0, 0), size/2, facecolor='gray', alpha=0.5, edgecolor='w',
                    label=f'置信度: {size}')
    for size in sizes
]
ax1.legend(handles=legend_elements, loc='upper right', title='置信度')

# 绘制热力图（特征相关性矩阵）
im = ax2.imshow(corr_matrix, cmap='coolwarm', vmin=-1, vmax=1)

# 添加文本标注
for i in range(corr_matrix.shape[0]):
    for j in range(corr_matrix.shape[1]):
        text_color = 'white' if abs(corr_matrix[i, j]) > 0.5 else 'black'
        ax2.text(j, i, f'{corr_matrix[i, j]:.2f}',
                 ha='center', va='center', color=text_color, fontsize=10)

# 设置热力图标题和坐标轴
ax2.set_title('特征相关性热力图', fontsize=15, pad=20)
ax2.set_xticks(np.arange(10))
ax2.set_yticks(np.arange(10))
ax2.set_xticklabels([f'特征{i+1}' for i in range(10)], rotation=45, ha='right')
ax2.set_yticklabels([f'特征{i+1}' for i in range(10)])

# 添加颜色条
cbar = plt.colorbar(im, ax=ax2)
cbar.set_label('相关系数', rotation=270, labelpad=20)

# 调整布局并保存
plt.tight_layout(pad=4.0)
plt.savefig('scatter_heatmap_demo.png', dpi=300, bbox_inches='tight')
plt.show()

在使用散点图时，点的大小和颜色编码是传递多维信息的关键：

• 颜色(c)：适合表示类别型或连续型变量

• 大小(s)：适合表示数值型变量，建议使用s = values * scale + min_size的形式避免过小的点不可见

• 透明度(alpha)：数据点密集时建议设置为0.5~0.7，减少重叠掩盖

热力图的视觉效果很大程度上依赖于颜色映射(cmap)的选择：

• 发散型颜色映射（如coolwarm）：适合有正负方向的数值（如相关系数）

• 顺序型颜色映射（如viridis）：适合单调递增的数值（如概率分布）

• 定性颜色映射（如tab10）：适合类别型数据

自定义样式与高级功能

图表样式深度定制

Matplotlib提供了细粒度的图表样式控制能力，从整体风格到局部细节均可精确调整。掌握样式定制不仅能使图表更符合特定场景需求，还能形成统一的可视化风格，提升专业度和品牌识别度。Matplotlib 3.x版本引入的style系统支持通过预定义样式表或自定义配置文件快速切换图表风格。

以下代码展示了如何创建和应用自定义样式，以及如何精确控制图表的各种视觉元素：

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.ticker import MultipleLocator, FormatStrFormatter

# 设置中文字体
plt.rcParams["font.family"] = ["SimHei", "WenQuanYi Micro Hei", "Heiti TC"]
plt.rcParams['axes.unicode_minus'] = False

# 定义自定义样式
custom_style = {
    # 字体设置
    'font.family': ['SimHei', 'WenQuanYi Micro Hei', 'Heiti TC'],
    'font.size': 12,
    'axes.titlesize': 16,
    'axes.labelsize': 14,
    'xtick.labelsize': 11,
    'ytick.labelsize': 11,
    'legend.fontsize': 12,

    # 颜色设置
    'axes.facecolor': '#f8f9fa',  # 坐标轴背景色
    'figure.facecolor': 'white',   # 图表背景色
    'axes.edgecolor': '#d0d0d0',   # 坐标轴边框色

    # 网格线设置
    'grid.color': '#e0e0e0',
    'grid.linestyle': '--',
    'grid.linewidth': 0.8,

    # 线条设置
    'lines.linewidth': 2.0,
    'lines.markersize': 6,

    # 图例设置
    'legend.frameon': True,
    'legend.framealpha': 0.8,
    'legend.facecolor': 'white',
    'legend.edgecolor': '#d0d0d0'
}

# 应用自定义样式
plt.style.use(custom_style)

# 生成示例数据
x = np.linspace(0, 10, 100)
y1 = np.sin(x)
y2 = np.cos(x)
y3 = np.sin(x) * np.exp(-0.1 * x)  # 衰减正弦曲线

# 创建图表和坐标轴
fig, ax = plt.subplots(figsize=(10, 6))

# 绘制多条曲线
line1, = ax.plot(x, y1, color='#2c7fb8', linestyle='-', marker='o',
                 markevery=10, label='正弦曲线')
line2, = ax.plot(x, y2, color='#d95f02', linestyle='--', marker='s',
                 markevery=10, label='余弦曲线')
line3, = ax.plot(x, y3, color='#1a9850', linestyle='-.', marker='^',
                 markevery=10, label='衰减正弦曲线')

# 自定义坐标轴刻度
ax.xaxis.set_major_locator(MultipleLocator(2))  # 主刻度间隔为2
ax.xaxis.set_minor_locator(MultipleLocator(0.5))  # 次刻度间隔为0.5
ax.yaxis.set_major_locator(MultipleLocator(0.5))
ax.yaxis.set_minor_locator(MultipleLocator(0.25))

# 设置刻度标签格式
ax.xaxis.set_major_formatter(FormatStrFormatter('%.1f'))
ax.yaxis.set_major_formatter(FormatStrFormatter('%.2f'))

# 自定义坐标轴外观
ax.tick_params(axis='both', which='major', length=6, width=1.5,
               direction='in', pad=10)
ax.tick_params(axis='both', which='minor', length=3, width=1,
               direction='in')

# 添加参考线
ax.axhline(0, color='gray', linestyle='-', linewidth=1)
ax.axvline(np.pi/2, color='red', linestyle=':', linewidth=1.5,
           label='π/2参考线')

# 设置标题和坐标轴标签
ax.set_title('自定义样式的三角函数曲线展示', pad=20)
ax.set_xlabel('X轴', labelpad=10)
ax.set_ylabel('Y轴', labelpad=10)

# 设置坐标轴范围
ax.set_xlim(0, 10)
ax.set_ylim(-1.2, 1.2)

# 添加网格线
ax.grid(True, which='major')
ax.grid(True, which='minor', linestyle=':', alpha=0.4)

# 自定义图例
legend = ax.legend(loc='upper right', frameon=True, ncol=2,
                   borderaxespad=0.5, columnspacing=1.5)
legend.get_frame().set_boxstyle('round,pad=0.3')  # 圆角边框

# 添加文本注释
ax.annotate('衰减趋势', xy=(6, y3[60]), xytext=(7, -0.5),
            arrowprops=dict(facecolor='black', shrink=0.05, width=1.5),
            fontsize=12, fontstyle='italic')

# 调整布局并添加水印
plt.tight_layout()
fig.text(0.5, 0.01, '数据可视化示例 © 2023', ha='center',
         alpha=0.3, fontsize=12)

# 保存图表
plt.savefig('custom_style_demo.png', dpi=300, bbox_inches='tight')
plt.show()

常用的预定义样式包括：

• 'default'：默认样式

• 'seaborn-v0_8-whitegrid'：带网格的简洁样式

• 'ggplot'：模仿R语言ggplot2的样式

• 'bmh'：Bayesian Methods for Hackers书籍使用的样式

• 'dark_background'：深色背景，适合演示场景

可以通过plt.style.available查看所有可用样式，通过plt.style.use(['style1', 'style2'])组合使用多个样式。对于需要在团队或项目中统一使用的样式，建议创建自定义样式文件（.mplstyle），包含所有样式配置项，然后通过plt.style.use('path/to/custom.style')加载使用。

多子图布局与复杂排版

在实际数据分析中经常需要将多个相关图表组合展示，以呈现完整的分析视角。Matplotlib提供了灵活的子图布局机制，支持从简单网格到复杂不规则布局的各种排列方式。掌握多子图布局技术能够显著提升数据故事的表达效果，使读者能够直观地比较不同维度的数据特征。

以下代码展示了多种高级子图布局技巧，包括嵌套子图、不等大小子图和共享坐标轴等高级功能：

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.gridspec import GridSpec

# 设置中文字体
plt.rcParams["font.family"] = ["SimHei", "WenQuanYi Micro Hei", "Heiti TC"]
plt.rcParams['axes.unicode_minus'] = False

# 生成示例数据
np.random.seed(42)
x = np.linspace(0, 10, 100)
y1 = np.sin(x)
y2 = np.cos(x)
y3 = np.random.normal(0, 1, 1000)
y4 = np.random.rand(5, 5)  # 5x5随机矩阵
y5 = np.cumsum(np.random.randn(100))  # 随机游走数据

# 创建复杂子图布局
fig = plt.figure(figsize=(14, 12))

# 使用GridSpec创建灵活布局
gs = GridSpec(3, 3, figure=fig,
              width_ratios=[1, 1, 0.8],  # 列宽比例
              height_ratios=[1, 1, 1],   # 行高比例
              wspace=0.3,  # 列间距
              hspace=0.4)  # 行间距

# 创建子图对象
ax1 = fig.add_subplot(gs[0, :2])  # 第1行，第1-2列
ax2 = fig.add_subplot(gs[0, 2])   # 第1行，第3列
ax3 = fig.add_subplot(gs[1, 0])   # 第2行，第1列
ax4 = fig.add_subplot(gs[1, 1])   # 第2行，第2列
ax5 = fig.add_subplot(gs[1, 2])   # 第2行，第3列
ax6 = fig.add_subplot(gs[2, :])   # 第3行，所有列

# 绘制子图1：正弦曲线
ax1.plot(x, y1, color='#1f77b4', linewidth=2)
ax1.set_title('(a) 正弦函数曲线', fontsize=13, pad=15)
ax1.set_xlabel('X值', fontsize=11)
ax1.set_ylabel('sin(X)', fontsize=11)
ax1.grid(True, linestyle='--', alpha=0.6)

# 绘制子图2：余弦曲线的频率分布
ax2.hist(y2, bins=15, orientation='horizontal', color='#ff7f0e', alpha=0.7)
ax2.set_title('(b) 余弦值分布', fontsize=13, pad=15)
ax2.set_xlabel('频率', fontsize=11)
ax2.set_ylabel('cos(X)', fontsize=11)

# 绘制子图3：散点图
ax3.scatter(x, y1, c=y2, cmap='viridis', alpha=0.7, edgecolor='w')
ax3.set_title('(c) sin(X) vs cos(X)', fontsize=13, pad=15)
ax3.set_xlabel('X值', fontsize=11)
ax3.set_ylabel('sin(X)', fontsize=11)
ax3.grid(True, linestyle='--', alpha=0.6)

# 绘制子图4：热力图
im = ax4.imshow(y4, cmap='coolwarm', interpolation='nearest')
ax4.set_title('(d) 随机矩阵热力图', fontsize=13, pad=15)
plt.colorbar(im, ax=ax4, shrink=0.8)
ax4.set_xticks([])  # 隐藏刻度
ax4.set_yticks([])

# 绘制子图5：箱线图
ax5.boxplot(y3, vert=False, patch_artist=True,
            boxprops=dict(facecolor='#2ca02c', alpha=0.7))
ax5.set_title('(e) 正态分布数据', fontsize=13, pad=15)
ax5.set_xlabel('数值', fontsize=11)
ax5.set_yticks([])  # 隐藏Y轴刻度

# 绘制子图6：双Y轴折线图
ax6.plot(x, y1, color='#1f77b4', linewidth=2, label='sin(X)')
ax6.set_xlabel('X值', fontsize=12)
ax6.set_ylabel('sin(X)', fontsize=12, color='#1f77b4')
ax6.tick_params(axis='y', labelcolor='#1f77b4')
ax6.grid(True, linestyle='--', alpha=0.6)

# 创建共享X轴的第二个Y轴
ax6_twin = ax6.twinx()
ax6_twin.plot(x, y5, color='#d62728', linewidth=2, linestyle='--', label='随机游走')
ax6_twin.set_ylabel('随机游走值', fontsize=12, color='#d62728')
ax6_twin.tick_params(axis='y', labelcolor='#d62728')

# 合并图例
lines, labels = ax6.get_legend_handles_labels()
lines2, labels2 = ax6_twin.get_legend_handles_labels()
ax6.legend(lines + lines2, labels + labels2, loc='upper right')
ax6.set_title('(f) 多变量时间序列对比', fontsize=13, pad=15)

# 添加主标题
fig.suptitle('多子图布局综合示例', fontsize=18, y=0.95)

# 调整布局并保存
plt.tight_layout()
plt.subplots_adjust(top=0.9)  # 为suptitle留出空间
plt.savefig('subplots_layout_demo.png', dpi=300, bbox_inches='tight')
plt.show()

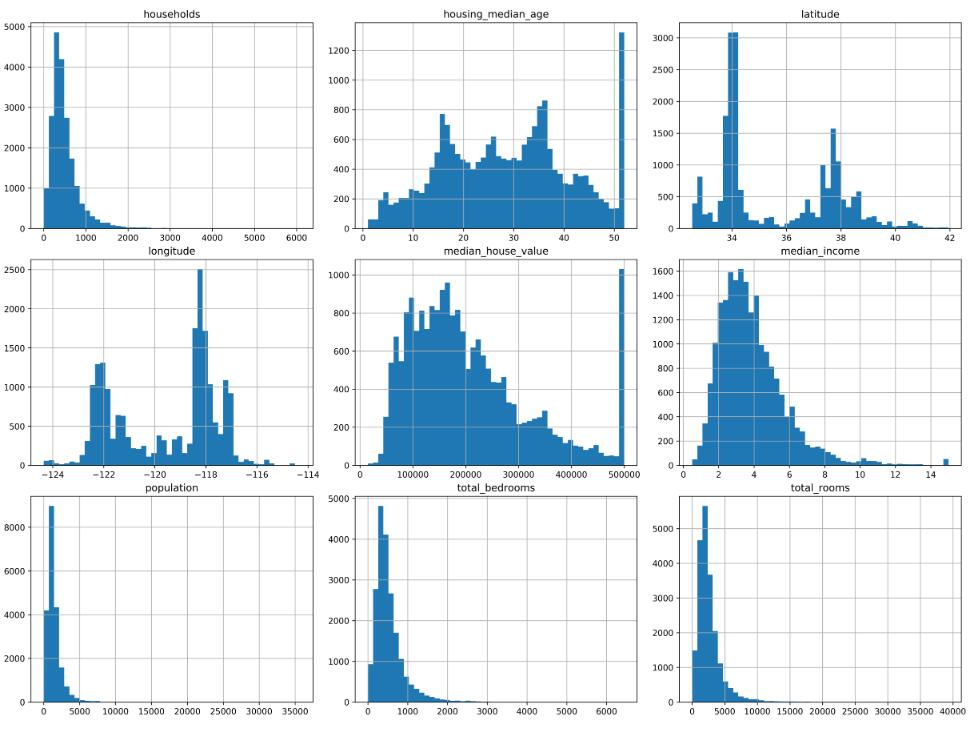
常用的子图创建方法对比：

方法	适用场景	优点	缺点
plt.subplots(nrows, ncols)	规则网格布局	简单直观，返回Axes数组	不支持复杂比例调整
fig.add_subplot(row, col, index)	灵活单张子图添加	可精确控制位置	需手动计算索引
GridSpec	复杂不规则布局	支持行列比例调整，可嵌套	语法稍复杂
subplot_mosaic	可视化布局定义	用字符串直观定义布局	Matplotlib 3.3+支持

对于需要高度定制的布局，推荐使用GridSpec，它支持通过width_ratios和height_ratios参数设置不同列/行的相对大小，通过wspace和hspace控制间距，还可以通过切片操作创建跨行列的子图。

多子图布局时的实用技巧：

• 使用一致的配色方案和字体样式，增强整体协调性

• 为相关子图共享坐标轴，减少冗余信息

• 使用字母标签(a), (b), (c)标识子图，便于引用

• 复杂布局时使用constrained_layout=True自动调整元素间距

• 通过fig.suptitle()添加整体标题，概括子图组合的主题

3D可视化与交互功能

随着数据复杂度的增加，二维可视化有时难以充分展示数据的空间分布特征。Matplotlib的mplot3d工具包提供了完整的3D可视化能力，支持从不同视角观察数据的立体结构。在LLM开发中，3D可视化可用于展示高维嵌入空间、注意力权重分布、模型参数空间等复杂数据结构。

以下代码展示了多种3D图表类型的创建方法，以及如何添加交互功能增强数据探索体验：

import numpy as np
import matplotlib.pyplot as plt
from matplotlib import cm
from mpl_toolkits.mplot3d import Axes3D

# 设置中文字体
plt.rcParams["font.family"] = ["SimHei", "WenQuanYi Micro Hei", "Heiti TC"]
plt.rcParams['axes.unicode_minus'] = False

# 生成3D数据
np.random.seed(42)

# 1. 3D曲面图数据
X = np.linspace(-5, 5, 100)
Y = np.linspace(-5, 5, 100)
X, Y = np.meshgrid(X, Y)
R = np.sqrt(X2 + Y2)
Z = np.sin(R) * np.cos(0.5 * X) * np.sin(0.5 * Y)  # 复杂波动曲面

# 2. 3D散点图数据（模拟嵌入空间）
num_points = 200
x_embed = np.random.normal(0, 1, num_points)
y_embed = np.random.normal(0, 1, num_points)
z_embed = np.random.normal(0, 1, num_points)
categories = np.random.randint(0, 5, num_points)  # 5个类别
sizes = np.random.uniform(50, 200, num_points)    # 随机点大小

# 创建2x2的3D子图布局
fig = plt.figure(figsize=(14, 12))

# 子图1：3D曲面图
ax1 = fig.add_subplot(221, projection='3d')
surf = ax1.plot_surface(
    X, Y, Z,
    cmap=cm.coolwarm,
    alpha=0.8,
    linewidth=0,
    antialiased=True,
    rstride=2, cstride=2  # 降低采样密度，提高渲染速度
)
ax1.set_title('(a) 3D曲面图', fontsize=14, pad=20)
ax1.set_xlabel('X轴', fontsize=11)
ax1.set_ylabel('Y轴', fontsize=11)
ax1.set_zlabel('Z轴', fontsize=11)
fig.colorbar(surf, ax=ax1, shrink=0.7, aspect=8)
ax1.view_init(elev=30, azim=45)  # 设置初始视角

# 子图2：3D散点图（嵌入空间可视化）
ax2 = fig.add_subplot(222, projection='3d')
scatter = ax2.scatter(
    x_embed, y_embed, z_embed,
    c=categories,
    s=sizes,
    cmap='viridis',
    alpha=0.7,
    edgecolors='w',
    linewidth=0.5
)
ax2.set_title('(b) 3D嵌入空间散点图', fontsize=14, pad=20)
ax2.set_xlabel('维度1', fontsize=11)
ax2.set_ylabel('维度2', fontsize=11)
ax2.set_zlabel('维度3', fontsize=11)
fig.colorbar(scatter, ax=ax2, shrink=0.7, aspect=8, label='类别')
ax2.view_init(elev=20, azim=60)

# 子图3：3D线框图
ax3 = fig.add_subplot(223, projection='3d')
wireframe = ax3.plot_wireframe(
    X, Y, Z,
    rstride=5, cstride=5,  # 网格步长
    color='#2ca02c',
    alpha=0.7,
    linewidth=0.8
)
ax3.set_title('(c) 3D线框图', fontsize=14, pad=20)
ax3.set_xlabel('X轴', fontsize=11)
ax3.set_ylabel('Y轴', fontsize=11)
ax3.set_zlabel('Z轴', fontsize=11)
ax3.view_init(elev=45, azim=120)

# 子图4：3D条形图
ax4 = fig.add_subplot(224, projection='3d')
# 生成条形图数据
x_bars = np.arange(8)
y_bars = np.arange(8)
x_bars, y_bars = np.meshgrid(x_bars, y_bars)
x_bars = x_bars.flatten()
y_bars = y_bars.flatten()
z_bars = np.zeros_like(x_bars)
dx = dy = 0.7
dz = np.random.randint(1, 10, size=x_bars.shape)  # 随机高度

# 为条形图生成渐变颜色
colors = cm.viridis(dz / dz.max())

# 绘制3D条形图
ax4.bar3d(
    x_bars, y_bars, z_bars,
    dx, dy, dz,
    color=colors,
    alpha=0.8,
    shade=True
)
ax4.set_title('(d) 3D条形图', fontsize=14, pad=20)
ax4.set_xlabel('X类别', fontsize=11)
ax4.set_ylabel('Y类别', fontsize=11)
ax4.set_zlabel('数值', fontsize=11)
ax4.set_xticks([])  # 简化刻度
ax4.set_yticks([])
ax4.view_init(elev=40, azim=30)

# 添加主标题
fig.suptitle('Matplotlib 3D可视化功能展示', fontsize=18, y=0.96)

# 调整布局并保存
plt.tight_layout()
plt.subplots_adjust(top=0.92)
plt.savefig('3d_visualization_demo.png', dpi=300, bbox_inches='tight')
plt.show()

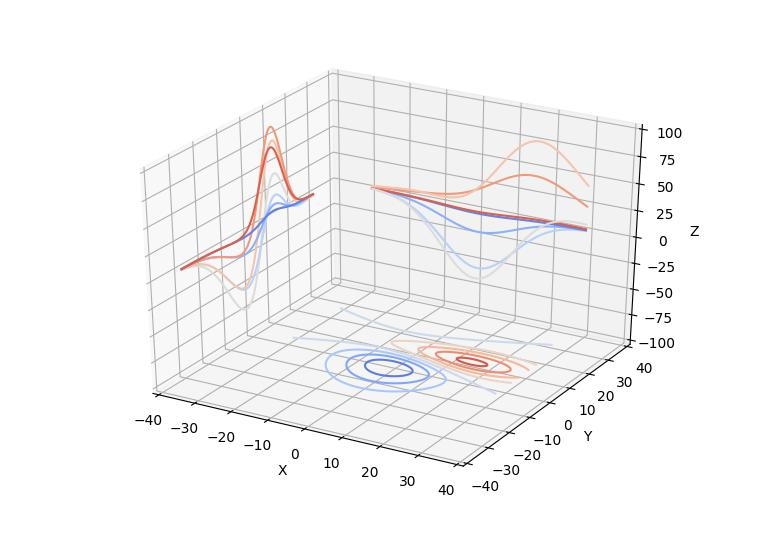
3D可视化的交互功能可以通过以下方式实现：

• 在Jupyter Notebook中使用%matplotlib notebook后端，支持鼠标交互旋转

• 使用ax.view_init(elev, azim)设置初始视角，elev为仰角，azim为方位角

• 对于复杂场景，可通过循环生成不同视角的图像，再合成为GIF动画

使用3D可视化时的注意事项：

• 避免过度使用3D效果，简单数据用2D展示更清晰

• 3D散点图点数量不宜过多，否则会显得杂乱

• 曲面图可通过rstride和cstride参数控制网格密度，平衡细节和性能

• 选择合适的初始视角，突出数据的关键特征

• 考虑使用透明度(alpha)增强深度感和层次关系

LLM开发实战案例

案例一：训练过程可视化与监控

在LLM模型训练过程中，实时监控关键指标的变化趋势对于评估模型进展、发现训练问题至关重要。Matplotlib提供了灵活的工具，可以将枯燥的数值日志转化为直观的可视化图表，帮助开发者快速识别过拟合、梯度消失、学习率不当等常见问题。

以下代码实现了一个完整的LLM训练监控可视化系统，支持多指标对比、动态更新和异常检测标注：

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.dates as mdates
from matplotlib.animation import FuncAnimation
from datetime import datetime, timedelta
import os

# 设置中文字体
plt.rcParams["font.family"] = ["SimHei", "WenQuanYi Micro Hei", "Heiti TC"]
plt.rcParams['axes.unicode_minus'] = False

# 模拟LLM训练日志数据
def generate_training_logs(num_steps=200):
    """生成模拟的LLM训练日志数据"""
    np.random.seed(42)

    # 时间轴（过去10小时）
    start_time = datetime.now() - timedelta(hours=10)
    timestamps = [start_time + timedelta(minutes=i*3) for i in range(num_steps)]

    # 基础损失曲线（指数衰减）
    base_loss = 3.5 * np.exp(-np.linspace(0, 3, num_steps))

    # 添加训练波动
    loss_fluctuation = np.random.normal(0, 0.15, num_steps)
    loss = base_loss + loss_fluctuation

    # 添加几个异常点（模拟训练不稳定）
    anomaly_indices = [50, 100, 150]
    loss[anomaly_indices] += np.random.uniform(0.5, 0.8, size=len(anomaly_indices))

    # 准确率曲线（S型增长）
    accuracy = 0.3 + 0.6 / (1 + np.exp(-(np.linspace(0, num_steps, num_steps) - num_steps/2)/20))
    accuracy += np.random.normal(0, 0.02, num_steps)
    accuracy = np.clip(accuracy, 0, 1)  # 确保在0-1范围内

    # 学习率调度（余弦退火）
    lr = 5e-5 * (1 + np.cos(np.linspace(0, np.pi, num_steps))) / 2

    # GPU利用率（波动较大）
    gpu_util = np.random.uniform(60, 95, num_steps)
    gpu_util = np.clip(gpu_util, 50, 100)

    return {
        'timestamps': timestamps,
        'steps': np.arange(1, num_steps+1),
        'loss': loss,
        'accuracy': accuracy,
        'lr': lr,
        'gpu_util': gpu_util,
        'anomalies': anomaly_indices
    }

# 生成模拟训练数据
logs = generate_training_logs()

# 创建训练监控仪表盘
fig, (ax1, ax2, ax3) = plt.subplots(3, 1, figsize=(12, 14), height_ratios=[2, 1, 1])

# 设置时间轴格式化器
date_formatter = mdates.DateFormatter('%H:%M')

# 绘制损失和准确率曲线（共享X轴）
line_loss, = ax1.plot(logs['timestamps'], logs['loss'], 'b-', linewidth=2, label='损失值')
ax1.set_ylabel('损失值', color='blue', fontsize=12)
ax1.tick_params(axis='y', labelcolor='blue')
ax1.grid(True, linestyle='--', alpha=0.6)

# 创建共享X轴的第二个Y轴（准确率）
ax1_twin = ax1.twinx()
line_acc, = ax1_twin.plot(logs['timestamps'], logs['accuracy'], 'g-', linewidth=2, label='准确率')
ax1_twin.set_ylabel('准确率', color='green', fontsize=12)
ax1_twin.tick_params(axis='y', labelcolor='green')
ax1_twin.set_ylim(0, 1.0)  # 准确率范围固定在0-1

# 合并图例
lines = [line_loss, line_acc]
labels = [l.get_label() for l in lines]
ax1.legend(lines, labels, loc='upper right', fontsize=11)

# 标注异常点
anomaly_timestamps = [logs['timestamps'][i] for i in logs['anomalies']]
anomaly_loss = [logs['loss'][i] for i in logs['anomalies']]
ax1.scatter(anomaly_timestamps, anomaly_loss, color='red', s=100, marker='*',
            label='训练异常', zorder=5)

# 设置标题和X轴格式
ax1.set_title('LLM训练过程监控仪表盘', fontsize=16, pad=20)
ax1.xaxis.set_major_formatter(date_formatter)

# 绘制学习率曲线
ax2.plot(logs['timestamps'], logs['lr'], 'r-', linewidth=2)
ax2.set_ylabel('学习率', color='red', fontsize=12)
ax2.tick_params(axis='y', labelcolor='red')
ax2.set_yscale('log')  # 对数刻度更适合学习率展示
ax2.grid(True, linestyle='--', alpha=0.6)
ax2.xaxis.set_major_formatter(date_formatter)

# 绘制GPU利用率
ax3.plot(logs['timestamps'], logs['gpu_util'], 'orange', linewidth=2)
ax3.set_ylabel('GPU利用率 (%)', color='orange', fontsize=12)
ax3.set_xlabel('训练时间', fontsize=12)
ax3.tick_params(axis='y', labelcolor='orange')
ax3.set_ylim(0, 105)
ax3.grid(True, linestyle='--', alpha=0.6)
ax3.xaxis.set_major_formatter(date_formatter)

# 添加统计信息文本框
stats_text = ax1.text(
    0.02, 0.02, '',
    transform=ax1.transAxes,
    bbox=dict(facecolor='white', alpha=0.8, boxstyle='round,pad=0.3')
)

# 更新统计信息
min_loss = np.min(logs['loss'])
max_acc = np.max(logs['accuracy'])
avg_gpu = np.mean(logs['gpu_util'])
stats_text.set_text(
    f'最小损失: {min_loss:.4f}\n'
    f'最大准确率: {max_acc:.4f}\n'
    f'平均GPU利用率: {avg_gpu:.1f}%'
)

# 添加异常点注释
for i, idx in enumerate(logs['anomalies']):
    ax1.annotate(
        f'异常点 #{i+1}',
        xy=(logs['timestamps'][idx], logs['loss'][idx]),
        xytext=(10, 10),
        textcoords='offset points',
        arrowprops=dict(arrowstyle='->', color='red'),
        fontsize=10,
        fontweight='bold',
        color='red'
    )

# 调整布局
plt.tight_layout(pad=3.0)

# 保存训练监控仪表盘
plt.savefig('llm_training_monitor.png', dpi=300, bbox_inches='tight')
plt.show()

# 模拟实时更新的训练动画（保存为GIF）
def create_training_animation(logs, save_path='training_animation.gif'):
    """创建训练过程动态演示动画"""
    fig, ax = plt.subplots(figsize=(10, 6))

    # 初始化曲线
    line_loss, = ax.plot([], [], 'b-', linewidth=2, label='损失值')
    ax.set_xlim(logs['timestamps'][0], logs['timestamps'][-1])
    ax.set_ylim(min(logs['loss'])*0.9, max(logs['loss'])*1.1)
    ax.set_xlabel('训练时间', fontsize=12)
    ax.set_ylabel('损失值', fontsize=12)
    ax.set_title('LLM训练损失动态变化', fontsize=14, pad=20)
    ax.grid(True, linestyle='--', alpha=0.6)
    ax.legend()
    ax.xaxis.set_major_formatter(date_formatter)

    # 添加实时状态文本
    status_text = ax.text(0.02, 0.95, '', transform=ax.transAxes,
                         bbox=dict(facecolor='white', alpha=0.8))

    def update(frame):
        """动画更新函数"""
        if frame == 0:
            return line_loss, status_text

        # 更新曲线数据
        line_loss.set_data(logs['timestamps'][:frame], logs['loss'][:frame])

        # 更新状态文本
        current_step = frame
        current_loss = logs['loss'][frame-1]
        status_text.set_text(f'步骤: {current_step}/{len(logs["steps"])}\n损失值: {current_loss:.4f}')

        return line_loss, status_text

    # 创建动画
    anim = FuncAnimation(
        fig, update, frames=len(logs['steps'])+1, interval=100, blit=True
    )

    # 保存为GIF（需要ffmpeg或 imagemagick支持）
    try:
        anim.save(save_path, writer='pillow', fps=10)
        print(f"训练动画已保存至 {save_path}")
    except Exception as e:
        print(f"保存动画时出错: {e}")

    plt.close(fig)

# 创建训练动画（实际运行时取消注释）
# create_training_animation(logs)

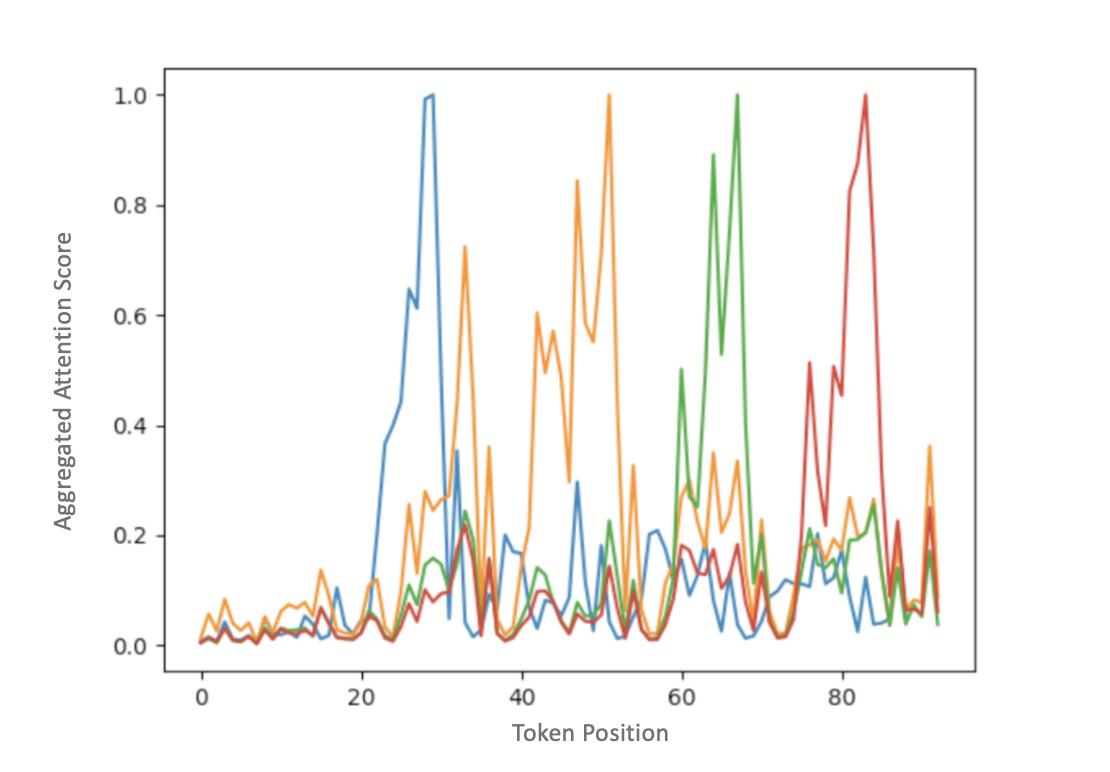
训练过程可视化的关键指标与监控要点：

指标类型	监控重点	异常模式	解决策略
损失值	整体下降趋势，波动幅度	突然上升，持续不下降	检查学习率，验证数据质量
准确率	增长趋势，收敛速度	停滞不前，波动过大	调整模型复杂度，增加训练数据
学习率	按计划变化，最终值	过早衰减，未按计划调整	修改学习率调度策略
GPU利用率	稳定性，峰值占比	频繁波动，持续100%	调整batch size，优化数据加载

在实际LLM训练中，建议结合TensorBoard等工具实现实时监控，但Matplotlib的优势在于可以高度定制图表样式，生成适合报告和展示的高质量静态图像。对于长时间运行的训练任务，可以编写定时执行的脚本，定期生成并保存监控图表，甚至通过邮件发送关键指标变化。

案例二：文本数据分布与特征可视化

大规模文本数据的特征分析是LLM开发的基础环节，通过可视化手段可以直观了解语料库的关键特征，如文本长度分布、词汇频率特征、语义相似度等。这些分析结果不仅能指导数据预处理策略，还能为模型架构设计提供重要参考。

以下代码实现了一个全面的文本数据特征可视化工具，涵盖从基础统计特征到高级语义特征的多维度分析：

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.colors as mcolors
from wordcloud import WordCloud
from sklearn.decomposition import PCA
from sklearn.manifold import TSNE
from collections import Counter
import string
import random

# 设置中文字体
plt.rcParams["font.family"] = ["SimHei", "WenQuanYi Micro Hei", "Heiti TC"]
plt.rcParams['axes.unicode_minus'] = False

# 模拟文本数据生成
def generate_synthetic_corpus(num_docs=5000):
    """生成模拟的文本语料库数据"""
    np.random.seed(42)

    # 主题类别
    topics = ['科技', '体育', '政治', '娱乐', '财经']

    # 每个主题的特征词汇
    topic_words = {
        '科技': ['人工智能', '机器学习', '算法', '数据', '计算机', '网络', '编程', '软件', '硬件', '技术'],
        '体育': ['比赛', '运动员', '足球', '篮球', '奥运会', '训练', '冠军', '教练', '团队', '得分'],
        '政治': ['政策', '政府', '法律', '选举', '领导人', '国家', '国际', '外交', '会议', '政策'],
        '娱乐': ['电影', '音乐', '明星', '节目', '演唱会', '电视剧', '奖项', '观众', '票房', '导演'],
        '财经': ['经济', '股票', '市场', '投资', '公司', '金融', '银行', '贸易', '货币', '增长']
    }

    # 通用词汇
    common_words = ['的', '是', '在', '有', '和', '就', '不', '人', '都', '一', '一个', '上', '也', '很', '到', '说', '要', '去', '你']

    # 生成文档特征
    docs = []
    doc_lengths = []
    doc_topics = []
    all_words = []

    for i in range(num_docs):
        # 随机选择主题
        topic = random.choice(topics)
        doc_topics.append(topic)

        # 生成文档长度（符合偏态分布）
        length = int(np.random.lognormal(4.5, 0.5))  # 对数正态分布，均值约100
        length = max(20, min(length, 500))  # 限制长度范围
        doc_lengths.append(length)

        # 生成文档内容
        doc_words = []
        # 主题相关词汇占比60%
        topic_word_count = int(length * 0.6)
        for _ in range(topic_word_count):
            word = random.choice(topic_words[topic])
            doc_words.append(word)
            all_words.append(word)

        # 通用词汇占比40%
        common_word_count = length - topic_word_count
        for _ in range(common_word_count):
            word = random.choice(common_words)
            doc_words.append(word)

        docs.append(' '.join(doc_words))

    # 生成模拟的词嵌入（300维）
    word_embeddings = {}
    for topic in topics:
        for word in topic_words[topic]:
            # 为每个主题的词生成聚类的嵌入
            mean_vec = np.random.randn(300) * 5  # 主题中心
            word_embeddings[word] = mean_vec + np.random.randn(300)  # 添加噪声

    return {
        'docs': docs,
        'doc_lengths': doc_lengths,
        'doc_topics': doc_topics,
        'word_counts': Counter(all_words),
        'word_embeddings': word_embeddings,
        'topics': topics
    }

# 生成模拟文本数据
corpus = generate_synthetic_corpus()

# 创建文本数据分析可视化
fig = plt.figure(figsize=(14, 16))
gs = fig.add_gridspec(3, 2, height_ratios=[1.2, 1.2, 1])

# 1. 文档长度分布
ax1 = fig.add_subplot(gs[0, 0])
n, bins, patches = ax1.hist(
    corpus['doc_lengths'], bins=30, color='#1f77b4', alpha=0.7, edgecolor='w'
)
ax1.set_title('(a) 文档长度分布', fontsize=14, pad=20)
ax1.set_xlabel('文本长度（词数）', fontsize=12)
ax1.set_ylabel('文档数量', fontsize=12)
ax1.grid(True, linestyle='--', alpha=0.6)

# 添加均值和中位数标记
mean_length = np.mean(corpus['doc_lengths'])
median_length = np.median(corpus['doc_lengths'])
ax1.axvline(mean_length, color='r', linestyle='--', linewidth=2,
            label=f'均值: {mean_length:.1f}')
ax1.axvline(median_length, color='g', linestyle='-.', linewidth=2,
            label=f'中位数: {median_length:.1f}')
ax1.legend(fontsize=11)

# 2. 主题分布饼图
ax2 = fig.add_subplot(gs[0, 1])
topic_counts = Counter(corpus['doc_topics'])
wedges, texts, autotexts = ax2.pie(
    topic_counts.values(), labels=topic_counts.keys(), autopct='%1.1f%%',
    colors=plt.cm.tab10.colors[:len(topic_counts)],
    textprops={'fontsize': 12},
    wedgeprops={'edgecolor': 'w', 'linewidth': 1}
)
ax2.set_title('(b) 文档主题分布', fontsize=14, pad=20)

# 3. 词云
ax3 = fig.add_subplot(gs[1, 0])
# 过滤低频词
filtered_words = {k: v for k, v in corpus['word_counts'].items() if v > 10}
wordcloud = WordCloud(
    font_path=None,  # 使用系统默认中文字体
    background_color='white',
    max_words=100,
    width=800, height=400,
    colormap='viridis'
).generate_from_frequencies(filtered_words)
ax3.imshow(wordcloud, interpolation='bilinear')
ax3.axis('off')
ax3.set_title('(c) 高频词汇云', fontsize=14, pad=20)

# 4. 词嵌入TSNE可视化
ax4 = fig.add_subplot(gs[1, 1])
# 获取词嵌入数据
words = list(corpus['word_embeddings'].keys())
embeddings = np.array([corpus['word_embeddings'][word] for word in words])
topics = []
for word in words:
    for topic, topic_words in topic_words.items():
        if word in topic_words:
            topics.append(topic)
            break

# 使用TSNE降维到2D
from sklearn.manifold import TSNE
tsne = TSNE(n_components=2, random_state=42, perplexity=10)
embeddings_2d = tsne.fit_transform(embeddings)

# 绘制散点图
scatter = ax4.scatter(
    embeddings_2d[:, 0], embeddings_2d[:, 1],
    c=[corpus['topics'].index(topic) for topic in topics],
    cmap='tab10', alpha=0.7, s=100, edgecolor='w'
)
ax4.set_title('(d) 词嵌入TSNE降维可视化', fontsize=14, pad=20)
ax4.set_xlabel('TSNE维度1', fontsize=11)
ax4.set_ylabel('TSNE维度2', fontsize=11)
ax4.grid(True, linestyle='--', alpha=0.6)

# 添加图例
legend1 = ax4.legend(
    handles=scatter.legend_elements()[0],
    labels=corpus['topics'],
    title="主题",
    loc="upper right"
)
ax4.add_artist(legend1)

# 5. 主题-长度关系箱线图
ax5 = fig.add_subplot(gs[2, :])
# 按主题分组的文档长度
topic_lengths = {}
for topic in corpus['topics']:
    topic_lengths[topic] = [
        corpus['doc_lengths'][i] for i, t in enumerate(corpus['doc_topics'])
        if t == topic
    ]

# 绘制箱线图
boxplot_data = [topic_lengths[topic] for topic in corpus['topics']]
boxprops = dict(linestyle='-', linewidth=2, color='black')
whiskerprops = dict(linestyle='--', linewidth=1.5, color='black')
medianprops = dict(linestyle='-', linewidth=2.5, color='red')

boxes = ax5.boxplot(
    boxplot_data, labels=corpus['topics'], patch_artist=True,
    boxprops=boxprops, whiskerprops=whiskerprops, medianprops=medianprops
)

# 设置箱体颜色
colors = plt.cm.tab10.colors[:len(corpus['topics'])]
for box, color in zip(boxes['boxes'], colors):
    box.set_facecolor(color)
    box.set_alpha(0.5)

ax5.set_title('(e) 不同主题的文档长度分布对比', fontsize=14, pad=20)
ax5.set_xlabel('主题', fontsize=12)
ax5.set_ylabel('文档长度（词数）', fontsize=12)
ax5.grid(True, linestyle='--', alpha=0.6, axis='y')

# 添加主标题
fig.suptitle('LLM训练数据特征分析', fontsize=18, y=0.98)

# 调整布局
plt.tight_layout()
plt.subplots_adjust(top=0.95)

# 保存可视化结果
plt.savefig('text_data_analysis.png', dpi=300, bbox_inches='tight')
plt.show()

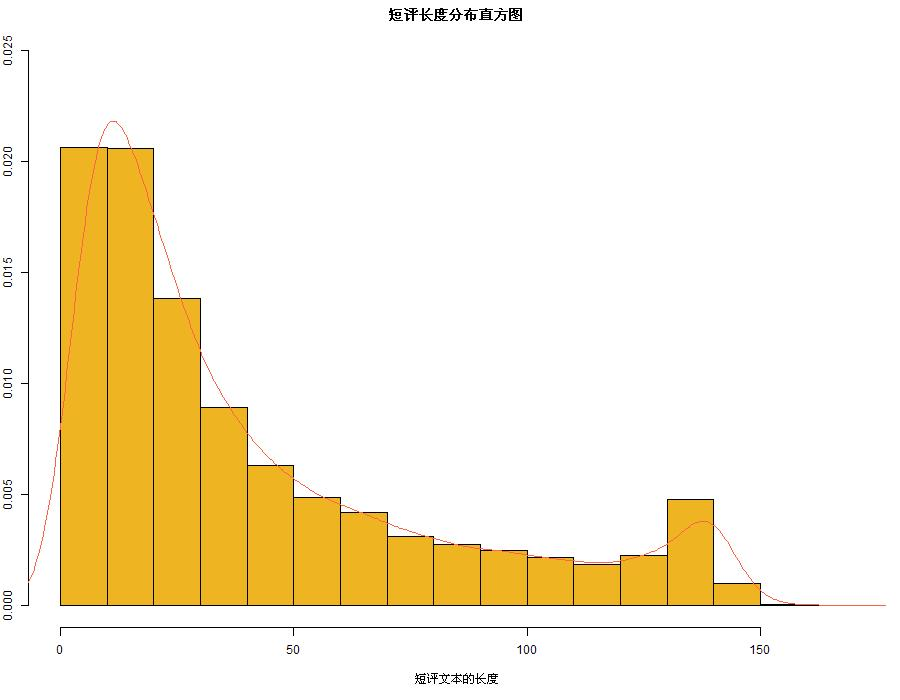
文本数据预处理建议：

1. 长度过滤：根据长度分布确定合理阈值，过滤过短（噪声）和过长（异常）文本

2. 主题均衡：检查主题分布，对样本不足的类别进行数据增强

3. 高频词分析：识别领域特定高频词，评估数据代表性

4. 低频词处理：对出现频率极低的词汇考虑替换或合并

5. 嵌入可视化：通过TSNE或UMAP检查词嵌入质量，验证语义聚类效果

案例三：模型推理结果对比与解释

LLM模型开发中，对不同模型或同一模型不同参数配置的推理结果进行客观对比分析是优化模型性能的关键环节。Matplotlib提供的多样化图表类型可以从多个维度直观展示模型的表现差异，并帮助开发者理解模型行为特征，定位改进方向。

以下代码实现了一个全面的LLM推理结果对比分析框架，涵盖响应质量评估、生成内容特征分析和注意力可视化等关键环节：

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.colors as mcolors
import seaborn as sns
from matplotlib.gridspec import GridSpec
import random

# 设置中文字体
plt.rcParams["font.family"] = ["SimHei", "WenQuanYi Micro Hei", "Heiti TC"]
plt.rcParams['axes.unicode_minus'] = False

# 模拟LLM推理结果数据
def generate_inference_results():
    """生成模拟的LLM推理结果对比数据"""
    np.random.seed(42)

    # 测试问题类型
    question_types = [
        '事实问答', '逻辑推理', '创意写作', '情感分析', '代码生成',
        '摘要生成', '翻译任务', '数学计算', '常识判断', '伦理问题'
    ]

    # 模型名称
    models = ['基础模型', '微调模型A', '微调模型B', '商业模型']

    # 生成质量评分数据（1-10分）
    quality_scores = {model: [] for model in models}
    for q_type in question_types:
        # 基础模型分数较低且波动大
        base_score = np.random.normal(6, 1.2)
        quality_scores['基础模型'].append(max(1, min(10, base_score)))

        # 微调模型A分数中等
        fine_tuned_a = base_score + np.random.normal(1.5, 0.8)
        quality_scores['微调模型A'].append(max(1, min(10, fine_tuned_a)))

        # 微调模型B在特定领域表现更好
        domain_boost = 2.0 if q_type in ['代码生成', '逻辑推理'] else 1.0
        fine_tuned_b = base_score + np.random.normal(1.2, 0.7) * domain_boost
        quality_scores['微调模型B'].append(max(1, min(10, fine_tuned_b)))

        # 商业模型整体表现最好但成本高
        commercial = base_score + np.random.normal(2.5, 0.5)
        quality_scores['商业模型'].append(max(1, min(10, commercial)))

    # 生成响应时间数据（秒）
    response_times = {model: [] for model in models}
    for _ in question_types:
        response_times['基础模型'].append(np.random.normal(1.2, 0.3))
        response_times['微调模型A'].append(np.random.normal(0.9, 0.2))
        response_times['微调模型B'].append(np.random.normal(1.0, 0.25))
        response_times['商业模型'].append(np.random.normal(0.7, 0.15))

    # 生成输出长度数据（词数）
    output_lengths = {model: [] for model in models}
    for q_type in question_types:
        base_length = np.random.normal(100, 30)
        output_lengths['基础模型'].append(max(20, int(base_length)))

        # 创意写作类生成更长文本
length_factor = 1.5 if q_type in ['创意写作', '摘要生成'] else 1.0
output_lengths['微调模型A'].append(max(20, int(base_length * 1.1 * length_factor)))
output_lengths['微调模型B'].append(max(20, int(base_length * 1.3 * length_factor)))
output_lengths['商业模型'].append(max(20, int(base_length * 1.2 * length_factor)))

# 生成模拟注意力权重矩阵
attention_weights = np.random.rand(len(question_types), len(question_types))
attention_weights = np.triu(attention_weights)  # 上三角矩阵

# 生成困惑度数据
perplexity = {model: [] for model in models}
for q_type in question_types:
    base_ppl = np.random.normal(8, 1.5)
    perplexity['基础模型'].append(max(1, base_ppl))
    perplexity['微调模型A'].append(max(1, base_ppl * 0.85))
    perplexity['微调模型B'].append(max(1, base_ppl * 0.8 * (0.7 if q_type in ['代码生成', '数学计算'] else 1.0)))
    perplexity['商业模型'].append(max(1, base_ppl * 0.7))

# 创建3x2的子图布局
fig, axes = plt.subplots(3, 2, figsize=(15, 18))
(ax1, ax2), (ax3, ax4), (ax5, ax6) = axes

# 1. 雷达图比较模型性能
from matplotlib.path import Path
from matplotlib.spines import Spine
from matplotlib.transforms import Affine2D

labels = question_types[:6]  # 取前6个问题类型
stats = {model: [np.mean(quality_scores[model][i::5]) for i in range(6)] for model in models}
angles = np.linspace(0, 2*np.pi, len(labels), endpoint=False).tolist()
angles += angles[:1]  # 闭合

for model, color in zip(models, ['#1f77b4', '#ff7f0e', '#2ca02c', '#d62728']):
    values = stats[model]
    values += values[:1]
    ax1.polar(angles, values, color=color, linewidth=2, label=model)
    ax1.fill(angles, values, color=color, alpha=0.25)

ax1.set_theta_offset(np.pi / 2)
ax1.set_theta_direction(-1)
ax1.set_thetagrids(np.degrees(angles[:-1]), labels)
ax1.set_ylim(0, 10)
ax1.set_title('不同模型在各类任务上的性能雷达图', fontsize=14, pad=20)
ax1.legend(loc='upper right', bbox_to_anchor=(1.3, 1.1))

# 2. 响应时间与质量散点图
for model, color in zip(models, ['#1f77b4', '#ff7f0e', '#2ca02c', '#d62728']):
    ax2.scatter(
        response_times[model], 
        quality_scores[model],
        c=color, alpha=0.7, s=100, label=model, edgecolor='w'
    )
ax2.set_xlabel('响应时间（秒）', fontsize=12)
ax2.set_ylabel('质量评分', fontsize=12)
ax2.set_title('模型响应时间与质量关系', fontsize=14, pad=20)
ax2.grid(True, linestyle='--', alpha=0.6)
ax2.legend()

# 3. 注意力权重热力图
im = ax3.imshow(attention_weights, cmap='viridis', vmin=0, vmax=1)
ax3.set_xticks(range(len(question_types)))
ax3.set_yticks(range(len(question_types)))
ax3.set_xticklabels(question_types, rotation=45, ha='right', fontsize=8)
ax3.set_yticklabels(question_types, fontsize=8)
ax3.set_title('模型注意力权重矩阵', fontsize=14, pad=20)
fig.colorbar(im, ax=ax3, shrink=0.8)

# 4. 困惑度箱线图
boxplot_data = [perplexity[model] for model in models]
ax4.boxplot(boxplot_data, labels=models, patch_artist=True,
            boxprops=dict(facecolor='#1f77b4', alpha=0.5))
ax4.set_ylabel('困惑度（越低越好）', fontsize=12)
ax4.set_title('不同模型的困惑度分布', fontsize=14, pad=20)
ax4.grid(True, linestyle='--', alpha=0.6, axis='y')

# 5. 输出长度小提琴图
violin_data = [output_lengths[model] for model in models]
ax5.violinplot(violin_data, showmeans=True)
ax5.set_xticks(range(1, len(models)+1))
ax5.set_xticklabels(models)
ax5.set_ylabel('输出长度（词数）', fontsize=12)
ax5.set_title('模型输出长度分布', fontsize=14, pad=20)
ax5.grid(True, linestyle='--', alpha=0.6, axis='y')

# 6. 成本效益分析气泡图
costs = [0.1, 0.3, 0.4, 1.0]  # 相对成本
avg_quality = [np.mean(quality_scores[model]) for model in models]
avg_speed = [np.mean(response_times[model]) for model in models]

bubble_sizes = [np.mean(output_lengths[model])/10 for model in models]
scatter = ax6.scatter(
    avg_speed, avg_quality, s=bubble_sizes,
    c=costs, cmap='coolwarm', alpha=0.7, edgecolor='w'
)
for i, model in enumerate(models):
    ax6.annotate(model, (avg_speed[i], avg_quality[i]),
                 xytext=(5, 5), textcoords='offset points')
ax6.set_xlabel('平均响应时间（秒）', fontsize=12)
ax6.set_ylabel('平均质量评分', fontsize=12)
ax6.set_title('模型成本效益分析（气泡大小=输出长度）', fontsize=14, pad=20)
fig.colorbar(scatter, ax=ax6, label='相对成本')
ax6.grid(True, linestyle='--', alpha=0.6)

# 调整布局并保存
plt.tight_layout(pad=4.0)
plt.savefig('llm_inference_comparison.png', dpi=300, bbox_inches='tight')
plt.show()