【机器学习】000_机器学习基本概念

最新推荐文章于 2024-12-08 00:04:21 发布

原创最新推荐文章于 2024-12-08 00:04:21 发布 · 191 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#机器学习 #人工智能

机器学习专栏收录该内容

45 篇文章

订阅专栏

一、机器学习的概念

· 定义：机器基于数据，去寻找一个对应的函数

二、机器学习的过程：

1. 写一个带有未知参数的函数表达式（基于研究领域的领域知识）

$y = wx+b$

其中，w, b（偏置）为未知的参数（权重），从数据中学习得到。

w：weight b:bias

这个带有未知参数的函数表示式就是模型（Model），x称为feature

2. 定义损失，定义训练数据的Loss函数

Loss是以前面提到的两个未知参数为参数的一个函数： $Loss(b,w)$

Loss函数的作用是衡量这组数据的好坏，具体的机制如下所示：

$Loss(0.5k, 1)$ $y = 0.5k+x$

将已知的一个 $x$ 代入，得到一个预测的 $y_{1}$ —— $y_{1}$ 和真实的值是有一定差距的。

我们可以计算出误差 $e_{1}=\left | y-y_{1} \right |$ ，同理我们可以算出已知所有 $x$ 值对应的误差 $e_{n}$ 。

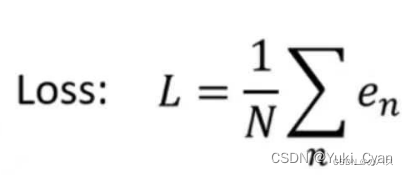
误差有两种计算方法：

$e = |y-y_{_{1}}|$ L is mean absolute error(MAE)

$e = (y - y_{1})^2$ L is mean square error(MSE)

如果 $y$ 和 $y_{1}$ 都是几率分布的，使用交叉熵。

用不同的 $w$ , $b$ 计算Loss画出等高线图，可以得到如下图（Error Surface）所示的结果：

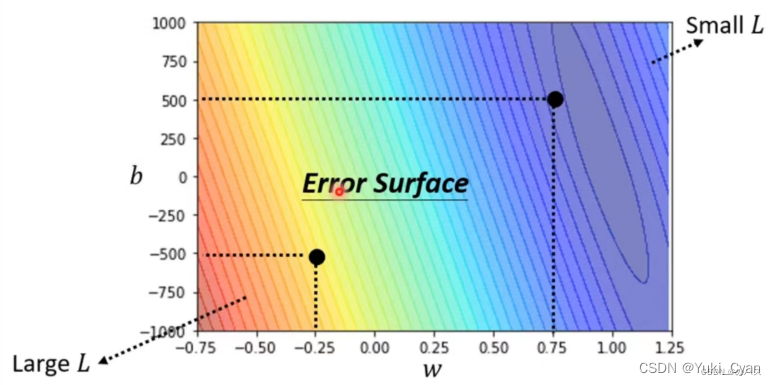
等高线越偏红色系，说明Loss值更大，这组的 $w$ , $b$ 效果更差；

越偏蓝色系，说明Loss值更小，这组的 $w$ , $b$ 效果越好；放到模型里得到的预测更精确。

3. 最佳化

找到合适的一组 $w$ , $b$ , 带到Loss函数里面，让计算所得的L值最小。

$w,b = arg min L$

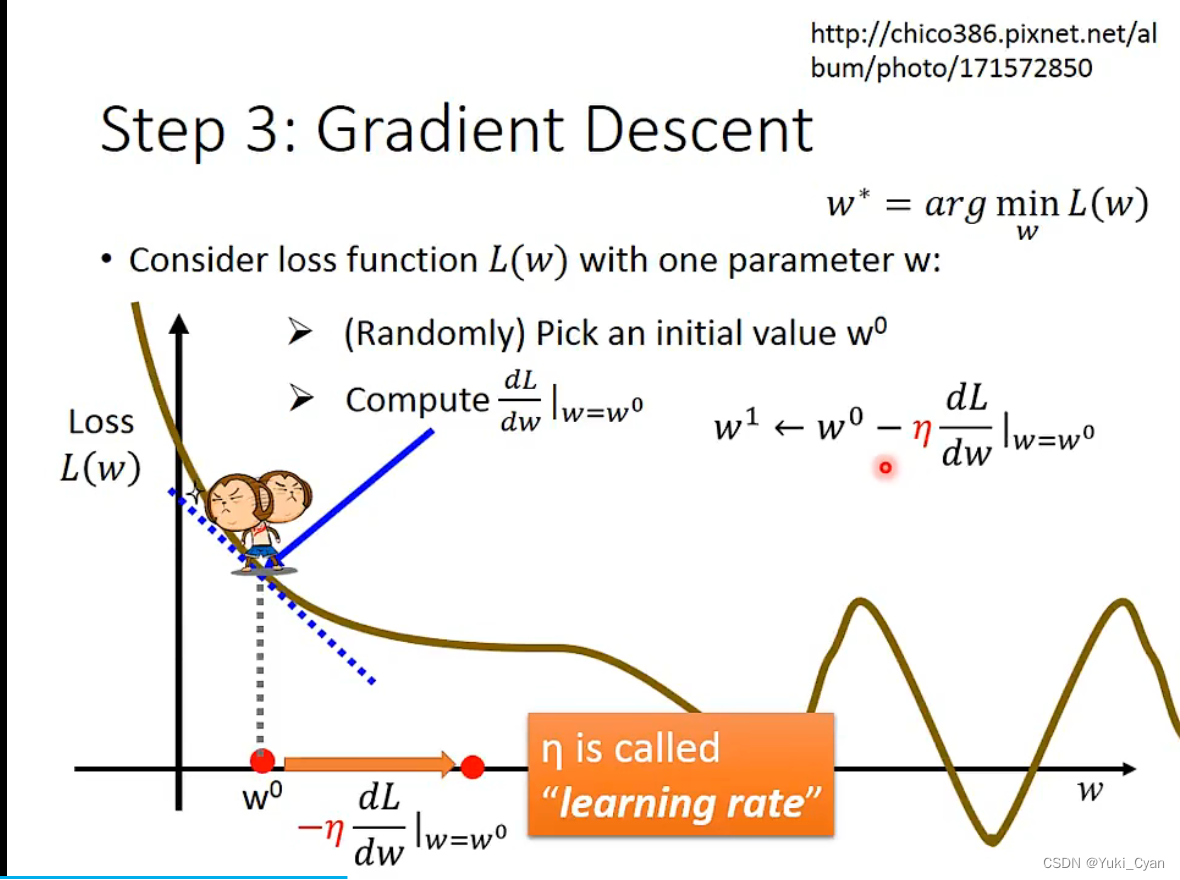
那具体怎么做呢？我们会用到Gradient Descent

（梯度下降：一种一阶迭代优化算法，用于寻找可微函数的局部最小值。）

先只看 $w$ 一个变量：

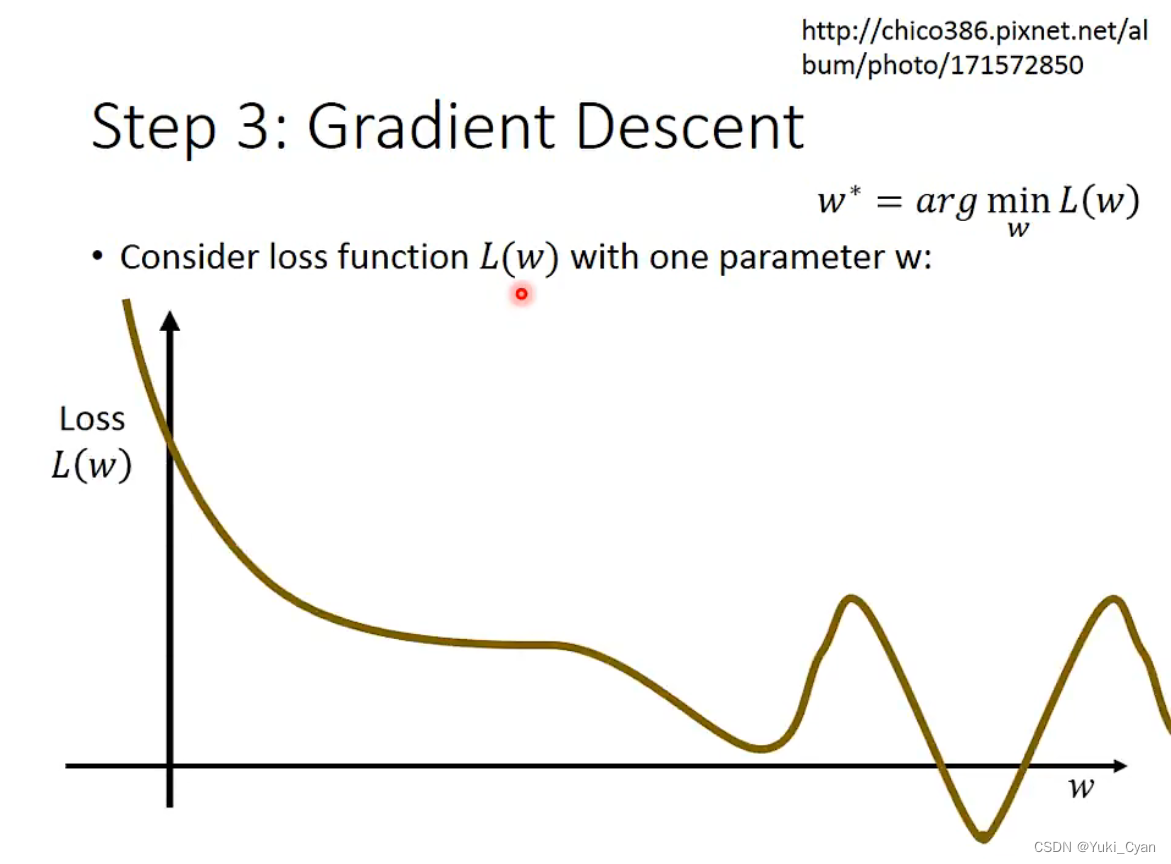
对于不同的 $w$ , 可以计算出不同的L值：

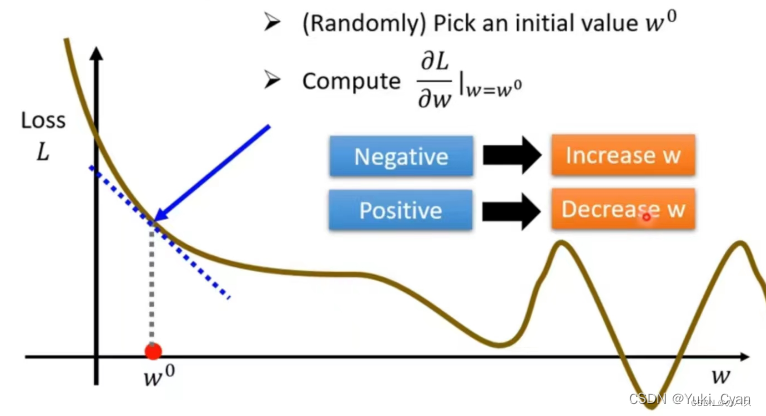
第一步：随机选取一个点 $w_{0}$ , 计算该点的微分，得到该点斜率；

第二步：判断该点斜率：正，减小 $w$ ；负，增大 $w$ （改变的幅度由定义的比率数值决定）

※ 比率数值 $\eta$ 称为“学习率”，是需要自己定义的变量，即hyperparameters（超参数）

第三步：迭代更新 $w$ , 直到找到斜率为0的点所对应的 $w$ 值。

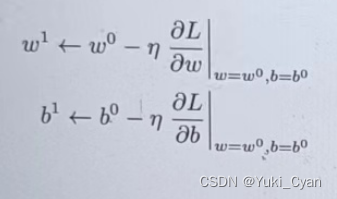
—> 分别求损失L对 $w,b$ 的偏导数，然后再乘以学习率 $\eta$ （自定义参数），在原有 $w_{0}$ 的基础上减去 $\eta$ * 偏导数。

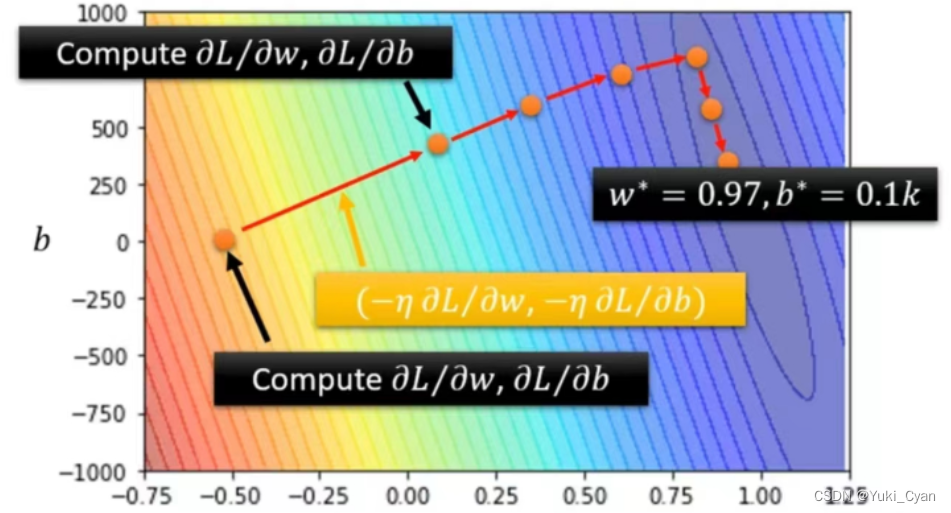
在Error Surface上的过程体现↑

三、一些专有名词

模型（model）：计算机层面的认知
学习算法（learning algorithm），从数据中产生模型的方法
数据集（data set）：一组记录的合集
示例（instance）：对于某个对象的描述
样本（sample）：也叫示例
属性（attribute）：对象的某方面表现或特征
特征（feature）：同属性
属性值（attribute value）：属性上的取值
属性空间（attribute space）：属性张成的空间
样本空间/输入空间（samplespace）：同属性空间
特征向量（feature vector）：在属性空间里每个点对应一个坐标向量，把一个示例称作特征向量
维数（dimensionality）：描述样本参数的个数（也就是空间是几维的）
学习（learning）/训练（training）：从数据中学得模型
训练数据（training data）：训练过程中用到的数据
训练样本（training sample）:训练用到的每个样本
训练集（training set）：训练样本组成的集合
假设（hypothesis）：学习模型对应了关于数据的某种潜在规则
真相（ground-truth）:真正存在的潜在规律
学习器（learner）：模型的另一种叫法，把学习算法在给定数据和参数空间的实例化
预测（prediction）：判断一个东西的属性
标记（label）：关于示例的结果信息，比如我是一个“好人”。
样例（example）：拥有标记的示例
标记空间/输出空间（label space）：所有标记的集合
分类（classification）：预测是离散值，比如把人分为好人和坏人之类的学习任务
回归（regression）：预测值是连续值，比如你的好人程度达到了0.9，0.6之类的
二分类（binary classification）：只涉及两个类别的分类任务
正类（positive class）：二分类里的一个
反类（negative class）：二分类里的另外一个
多分类（multi-class classification）：涉及多个类别的分类
测试（testing）：学习到模型之后对样本进行预测的过程
测试样本（testing sample）：被预测的样本
聚类（clustering）：把训练集中的对象分为若干组
簇（cluster）：每一个组叫簇
监督学习（supervised learning）：典范–分类和回归
无监督学习（unsupervised learning）：典范–聚类
未见示例（unseen instance）：“新样本“，没训练过的样本
泛化（generalization）能力：学得的模型适用于新样本的能力
分布（distribution）：样本空间的全体样本服从的一种规律
独立同分布（independent and identically distributed，简称i,i,d.）:获得的每个样本都是独立地从这个分布上采样获得的。