动态规划(01背包问题)

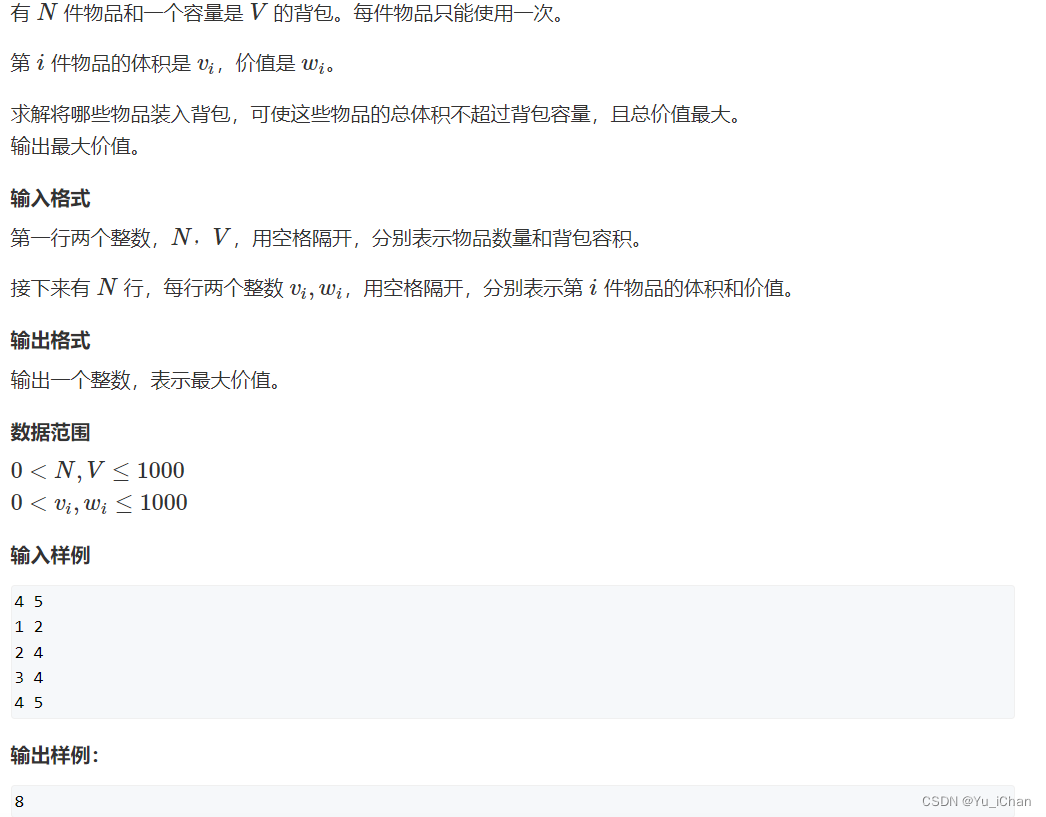
 首先动态规划分为状态表示、状态计算 

状态表示划分为一个集合以及一个集合的属性这里我们用f[i][j]表示选前i个物品，体积不超过j的价值集合，那么题目要我们求的是最大价值，所以最大价值就是属性

状态计算，也就是划分我们的集合来计算最大值

f[i][j]可以划分为两种，一种是选第i个物品，另一种是不选第i个物品

如果选第i个物品 那么我们的f[i][j]是不是可以转移成f[i-1][j-v[i]]+w[i]

不选的话 f[i][j]=f[i-1][j];

我们要在这两个中取值较大的那个就是我们的f[i][j]

#include<iostream>
using namespace std;

const int N=1010;

int f[N][N];
int w[N];
int v[N];
int n,m;

int main()
{
    cin>>n>>m;//输入物品数量以及背包体积
    for(int i=1;i<=n;i++)
    {
        cin>>v[i]>>w[i];
    }//输入每个物品的体积以及价值
    
    for(int i=1;i<=n;i++)
        for(int j=0;j<=m;j++)
        {
            f[i][j]=f[i-1][j];//不选第i个物品的时候的价值
            if(j>=v[i])f[i][j]=max(f[i][j],f[i-1][j-v[i]]+w[i]);//如果背包的体积够装下第i个物品就取其中最大值
        }
    cout<<f[n][m]<<endl;
    return 0;
}

我们还可以对上面的做法进行一个优化，把二维的f[i][j]优化成一维的

我们可以看到上面状态计算的时候实际上f[i][j]的转化都是用到了上一次的f[i-1][~],利用滚动数组的概念我们没有必要将f[i-1][~]这个状态存下来,我们可以直接去掉一维

用f[j]来表示f[j]就是前i轮已经决策的物品且背包容量 j下的最大价值。

那么我们是否可以直接去掉i-1这一维呢，答案是否定的，想想看，实际上我们去掉了，但是两重循环在这里i其实也就是第i轮，f[j]其实就是f[i-1][j]

去掉之后我们不能用背包体积的正序来更新f[j]，仔细看看去掉之后是如何更新的

f[j]=max(f[j],f[j-v[i]]+w[i]，更新的时候会用到f[j-v[i]]那么j-v[i]一定是小于j的，也就是说他要用到的实际上是f[i-1][j-v[i]]但是如果我们是从小体积往大体积更新的话，等到大体积更新的时候他的f[j-v[i]]实际上已经不是i-1层的了而是第i层

所以我们要做的就是给体积倒着更新

#include<iostream>
using namespace std;

const int N=1010;

int f[N];
int w[N];
int v[N];
int n,m;

int main()
{
    cin>>n>>m;//输入物品数量以及背包体积
    for(int i=1;i<=n;i++)
    {
        cin>>v[i]>>w[i];
    }//输入每个物品的体积以及价值
    
    for(int i=1;i<=n;i++)
        for(int j=m;j>=0;j--)
        {
            if(j>=v[i])f[j]=max(f[j],f[j-v[i]]+w[i]);//如果背包的体积够装下第i个物品就取其中最大值
        }
    cout<<f[m]<<endl;
    return 0;
}

然后又因为这个判断条件j>=v[i]我们可以接着优化循环

#include<iostream>
using namespace std;

const int N=1010;

int f[N];
int w[N];
int v[N];
int n,m;

int main()
{
    cin>>n>>m;//输入物品数量以及背包体积
    for(int i=1;i<=n;i++)
    {
        cin>>v[i]>>w[i];
    }//输入每个物品的体积以及价值
    
    for(int i=1;i<=n;i++)
        for(int j=m;j>=v[i];j--)
        {
            f[j]=max(f[j],f[j-v[i]]+w[i]);//如果背包的体积够装下第i个物品就取其中最大值
        }
    cout<<f[m]<<endl;
    return 0;
}