[USACO Dec21 Bronze]Air Cownditioning

最新推荐文章于 2024-02-29 22:21:16 发布

Black_Chocolate.

最新推荐文章于 2024-02-29 22:21:16 发布

阅读量514

点赞数 1

分类专栏：杂题集文章标签：算法 c++ 一维差分性质

本文链接：https://blog.youkuaiyun.com/YuDuna/article/details/128293466

版权

杂题集专栏收录该内容

24 篇文章

订阅专栏

本文通过一道具体题目，深入浅出地介绍了差分算法的应用场景及其实现方式。文章首先阐述了选择差分算法的原因，接着详细解释了如何利用差分技巧来解决这类问题，并给出了清晰的代码示例。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

复盘差分的时候，刷到了这道题，发现灰常巧妙，所以记录一下，发布一篇blog。供读者参考

题目链接：http://oj.daimayuan.top/course/22/problem/283

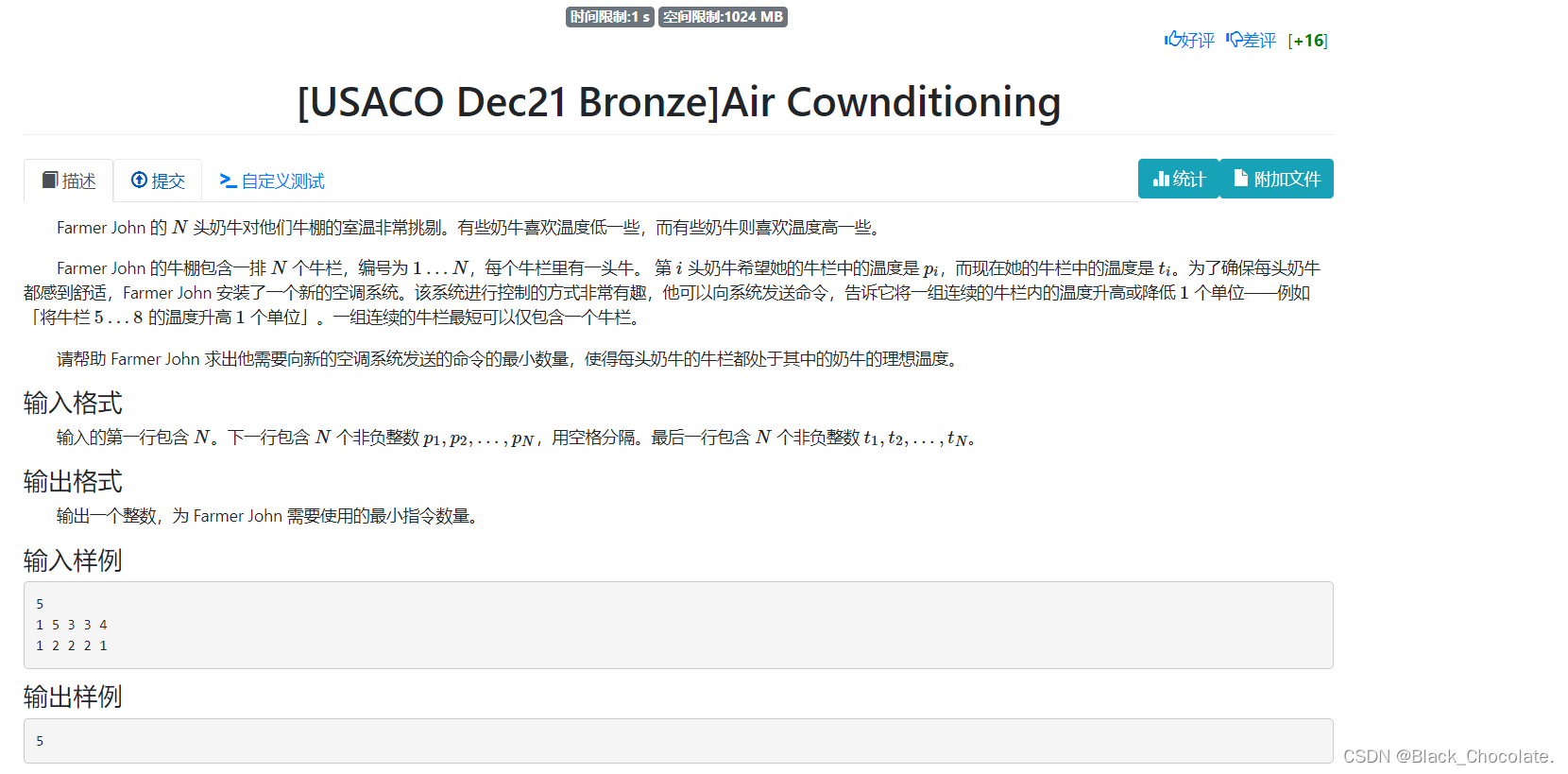
分析：为什么会选择用差分？

要使初始值往目标值进行调整，那么最坏的情况一定是它们的 |差值| 之和，即：每次选择一个牛棚进行温度调整。要使指令数量最少，那么就需要选择尽可能连续的区间，进行调整。

我们可以知道，调整完后的两个数组是相同的，即：他们的差值都为0.

如何进行调整？这里就需要差分。

怎样差分？

这里的差分数组D，用的是两个数组之间的差值进行构造的。

我们发现，改变一段连续的区间【L，R】，对于差分数组的操作即为：

D【L】+=1，D【R+1】-=1

要使得到达目标，我们就必须将D数组全部构造为0。这样才会满足调整完后的两个数组是相同的

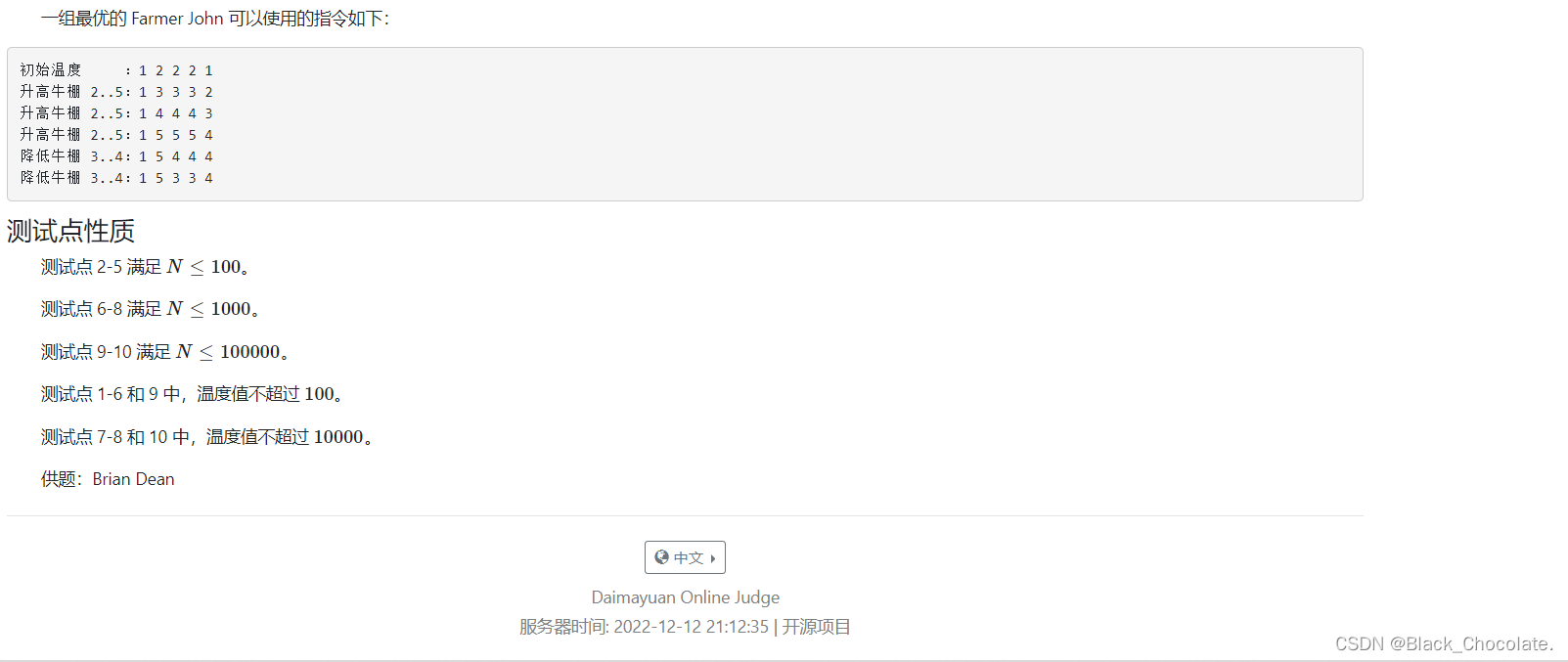
样例图解：

代码：

#include <bits/stdc++.h>
#define pi acos(-1)
#define int long long
#define PII pair<int,int>
#define all(v) v.begin(),v.end()
#define INF 0x3f3f3f3f3f3f3f3f
#define fs(a) cout<<fixed<<setprecision(a)<< //fs(4)(1.0/3)=0.3333//保留a位小数
#define read() freopen("input.txt","r",stdin)
#define output() freopen("output.txt","w",stdout)
#define fast ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
using namespace std;
const int N=2e6+10;
const int mod = 1e9+7;
const int Mod = 998244353;
int up(int a,int b){return a<0?a/b:(a+b-1)/b;}//       a/b向上取整
int n,a[N],b[N],c[N],d[N];

inline void solve(){
	cin>>n;
	for(int i=1;i<=n;i++) cin>>a[i];
	for(int i=1;i<=n;i++) cin>>b[i];
	for(int i=1;i<=n;i++) c[i]=a[i]-b[i];//差值数组
	for(int i=1;i<=n+1;i++) d[i]=c[i]-c[i-1];//差分数组
	int ans=0;
	for(int i=1;i<=n+1;i++) ans+=max(d[i],0LL);//+(D[i]>0）
	cout<<ans<<'\n';
}

signed main(){
	fast; solve();
}