算法基础课—数学知识（五）卡特兰数及其常见问题应用

最新推荐文章于 2022-09-27 19:25:19 发布

肥肥饼

最新推荐文章于 2022-09-27 19:25:19 发布

阅读量884

点赞数

分类专栏：算法基础课文章标签：数据结构算法

本文链接：https://blog.youkuaiyun.com/Yttttttttttttttt/article/details/117519162

版权

这篇博客探讨了卡特兰数在各种算法问题中的应用，包括满足条件的01序列、满二叉树个数、电影购票问题、进栈问题、圆内连弦、合法括号表达式个数以及凸多边形分割问题。文章通过实例和图解展示了如何将问题转化为卡特兰数问题，并提供了相关问题的解决方案和递推公式。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

关键

将问题转化成+1、-1序列，判断是否符合卡特兰数的条件
或者符合卡特兰数递归式

满足条件的01序列

题目

给定 n 个 0 和 n 个 1，它们将按照某种顺序排成长度为 2n 的序列，求它们能排列成的所有序列中，能够满足任意前缀序列中 0 的个数都不少于 1 的个数的序列有多少个。

输出的答案对 109+7 取模。

输入格式
共一行，包含整数 n。

输出格式
共一行，包含一个整数，表示答案。

数据范围
1≤n≤105
输入样例：
3
输出样例：
5

卡特兰数

任意一个0,1序列可转换成如下图所示的图，任意一个路径也可以转换对应的01序列
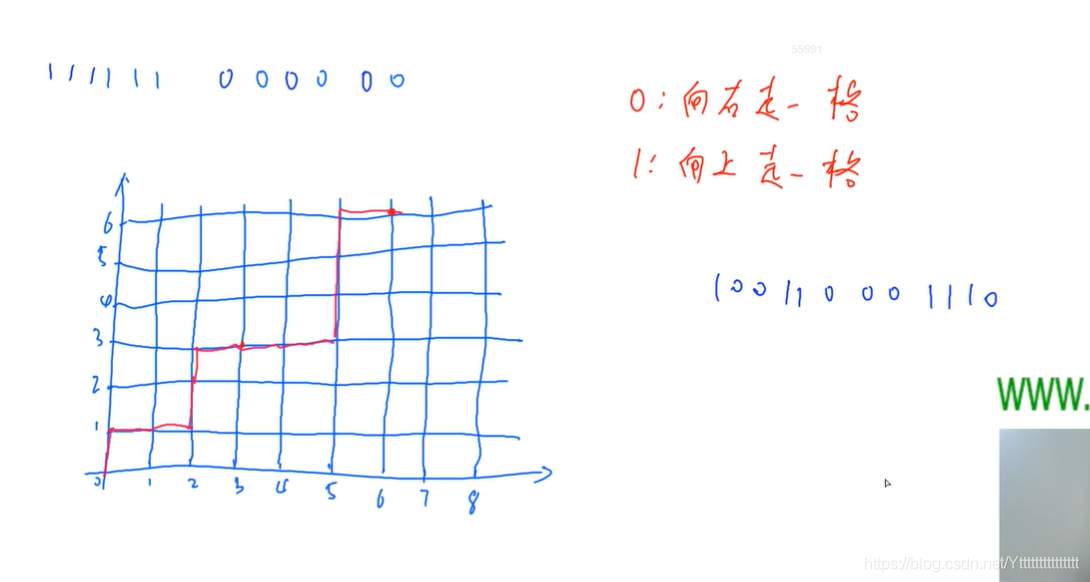
在这里插入图片描述

根据题目
所以我们所有的点都应该在这个红色这条边的下面
在这里插入图片描述

思路：任何一条从（0,0 ）走到（6,6）且经过红边的路径，我们将其到达红边的那个点关于红线做轴对称，会到达（5,7），变成一条从（0,0）走到（5,7）的路径。我们可以发现任意一条从（0,0）走到（5,7）的路径一定经过红线，所以我们对经过红线的点之后做轴对称，一定是一条从（0,0 ）走到（6,6）且经过红边的路径，所以那些不符合条件的数量就是C 5 12。
在这里插入图片描述

卡特兰数的推导
在这里插入图片描述

公式在右上角
在这里插入图片描述

对应组合数的第二种方法，用a，b的范围较大，所以先进行一步预处理，同时很多思想都把除法转换成逆元的形式。

模板

#include <iostream>
#include <algorithm>

using namespace std;

typedef long long LL;

const int N = 100010, mod = 1e9 + 7;


int qmi(int a, int k, int p)
{
   
    int res = 1;
    while (k)
    {
   
        if (k & 1) res = (LL)res * a % p;
        a = (LL)a * a % p;
        k >>=