108. 将有序数组转换为二叉搜索树【二叉树】

108. 将有序数组转换为二叉搜索树

108. 将有序数组转换为二叉搜索树

给你一个整数数组 nums ，其中元素已经按 升序 排列，请你将其转换为一棵
平衡二叉搜索树。

示例 1：

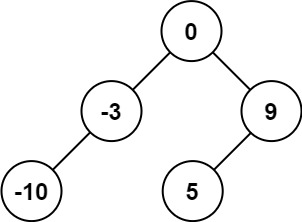
输入：nums = [-10,-3,0,5,9]
输出：[0,-3,9,-10,null,5]
解释：[0,-10,5,null,-3,null,9] 也将被视为正确答案：

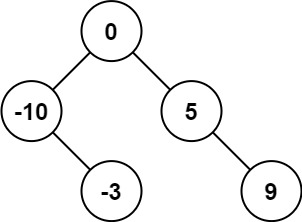
示例 2：

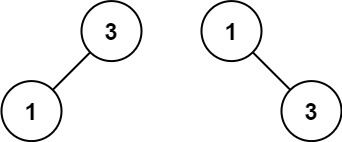
输入：nums = [1,3]
输出：[3,1]
解释：[1,null,3] 和 [3,1] 都是高度平衡二叉搜索树。

提示：

• 1 <= nums.length <= 10^4
• -10^4 <= nums[i] <= 10^4
• nums 按 严格递增 顺序排列

解题思路

由于是要构造平衡的二叉搜索树，所以两边的高度最多相差1，因此我们应该选数组的中间位置元素作为根节点，这样左右子树的元素个数才接近，且满足根节点大于左子树所有节点，小于右子树所有节点

Go代码

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func sortedArrayToBST(nums []int) *TreeNode {
    // 由于是要构造平衡的二叉搜索树，所以两边的高度最多相差1，因此我们应该选数组的中间位置元素作为根节点
    // 这样左右子树的元素才接近，且满足根节点大于左子树所有节点，小于右子树所有节点
    if len(nums) == 0 {
        return nil
    }
    // 左闭右闭
    root := dfs(nums,0,len(nums) - 1)
    return root

}

func dfs(nums []int,left,right int)*TreeNode{
    // 当前区间已经没有元素，可以递归结束返回nil,让上层递归的Left或者Right接住它
    if left > right {
        return nil
    }
    mid := left + (right - left) / 2
    root := &TreeNode{Val:nums[mid]}
    root.Left  = dfs(nums,left,mid - 1)
    root.Right = dfs(nums,mid+1,right)
    return root
}