450. 删除二叉搜索树中的节点【二叉树】

450. 删除二叉搜索树中的节点

450. 删除二叉搜索树中的节点

给定一个二叉搜索树的根节点root和一个值 key，删除二叉搜索树中的key对应的节点，并保证二叉搜索树的性质不变。返回二叉搜索树（有可能被更新）的根节点的引用。

一般来说，删除节点可分为两个步骤：

• 首先找到需要删除的节点；
• 如果找到了，删除它。

示例 1:

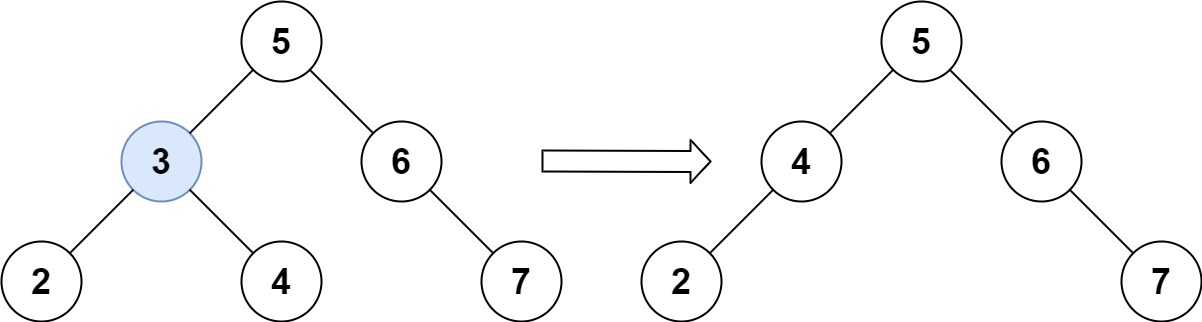
输入：root = [5,3,6,2,4,null,7], key = 3
输出：[5,4,6,2,null,null,7]
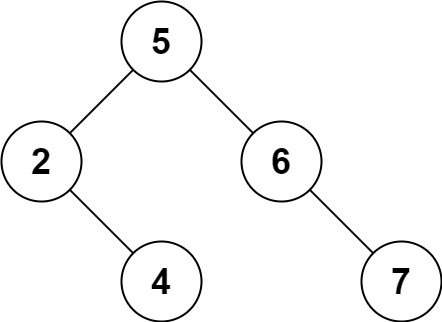
解释：给定需要删除的节点值是 3，所以我们首先找到 3 这个节点，然后删除它。 一个正确的答案是
[5,4,6,2,null,null,7], 如下图所示。 另一个正确答案是 [5,2,6,null,4,null,7]。

示例 2:

输入: root = [5,3,6,2,4,null,7], key = 0
输出: [5,3,6,2,4,null,7]
解释: 二叉树不包含值为 0 的节点

示例 3:

输入: root = [], key = 0
输出: []

提示:

• 节点数的范围 [0, 10^4].
• -10^5 <= Node.val <= 10^5
• 节点值唯一
• root 是合法的二叉搜索树
• -10^5 <= key <= 10^5

进阶： 要求算法时间复杂度为 O(h)，h 为树的高度。

解题思路

本人另一篇博客对该题有详解：https://blog.youkuaiyun.com/YouMing_Li/article/details/142663546

Go代码

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func deleteNode(root *TreeNode, key int) *TreeNode {
	// 第一种情况：没有找到要删除的节点，返回nil
    if root == nil {
        return nil
    }
    if root.Val == key {
   		 // 第二种情况：左右孩子都为空（叶子节点），直接删除节点， 返回nil
        if root.Left == nil && root.Right == nil {
            return nil
         // 第三种情况：其右孩子为空，左孩子不为空，删除节点，左孩子补位，返回左孩子
        } else if root.Left != nil && root.Right == nil {
            return root.Left
         // 第四种情况：其左孩子为空，右孩子不为空，删除节点，右孩子补位 ，返回右孩子
        } else if root.Left == nil && root.Right != nil {
            return root.Right
        }
        // 第五种情况：左右孩子节点都不为空，则将删除节点的左子树放到删除节点的右子树的最左面节点的左孩子的位置
    // 并返回删除节点右孩子
        temp := root.Right
        for temp.Left != nil {// 找右子树最左面的节点
            temp = temp.Left
        }
        // 把要删除的节点（root）左子树放在cur的左孩子的位置
        temp.Left = root.Left 
        return root.Right
    }
    // 这里相当于下层把新的节点返回给上一层，上一层就要用 root.Left 或者 root.Right接住
    if root.Val > key {
        root.Left = deleteNode(root.Left,key)
    }
    if root.Val < key {
        root.Right = deleteNode(root.Right,key)
    }
    return root
}