52. N 皇后 II 【回溯】

52. N 皇后 II

52. N 皇后 II

n 皇后问题 研究的是如何将 n 个皇后放置在 n × n 的棋盘上，并且使皇后彼此之间不能相互攻击。

给你一个整数n，返回n皇后问题 不同的解决方案的数量。

示例 1：

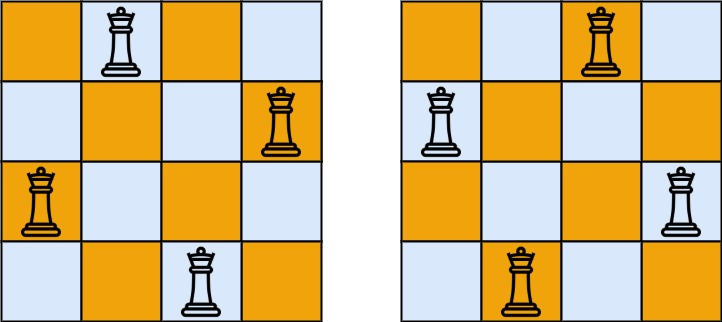
输入：n = 4
输出：2
解释：如上图所示，4 皇后问题存在两个不同的解法。

示例 2：

输入：n = 1
输出：1

提示：

• 1 <= n <= 9

解题思路

经典回溯问题，可以一行一行的放，看看每行的某个格子是否可以放皇后

Go代码

func totalNQueens(n int) int {
    // 经典回溯问题，可以一行一行的放，看看每行的某个格子是否可以放皇后
    if n <= 0 {
        return 0
    }
    // 初始化棋盘，初始每个格子是空串，放了皇后则当前格子置为“Q”
    board := make([][]string,n)
    for i := 0;i < len(board);i++ {{
        board[i] = make([]string,n)
    }}
    res := 0
    backtrack(board,0,&res)
    return res
}

func backtrack(board [][]string ,row int,res *int) {
    if row == len(board) { // 能把所有行都放一个皇后，说明找到了一个结果
        *res++
        return 
    }

    // 当前行每个格子尝试放皇后
    for j := 0;j < len(board[row]);j++{
        if !isValid(board,row,j){
            continue
        }
        board[row][j] = "Q"
        backtrack(board,row+1,res)
        board[row][j] = ""
    }
}

func isValid(board [][]string,row,col int) bool {
    // 当前行没有皇后
    for j := 0;j < col;j++ {
        if board[row][j] == "Q" {
            return false
        }
    }
    // 当前列没有皇后
    for i := 0;i < row;i++{
        if board[i][col] == "Q"{
            return false
        }
    }
    // 左上角45度没有皇后 i-1,j-1
    i,j := row-1,col-1
    for i >= 0 && j >= 0 {
        if board[i][j] == "Q"{
            return false
        }
        i--
        j--
    }

    // 右上角135度没有皇后 i-1,j+1
    i,j = row - 1,col + 1
    for i >=0 && j < len(board) {
        if board[i][j] == "Q" {
            return false
        }
        i--
        j++
    }

    return true
}