74 搜索二维矩阵

74. 搜索二维矩阵

编写一个高效的算法来判断 m x n 矩阵中，是否存在一个目标值。该矩阵具有如下特性：

• 每行中的整数从左到右按升序排列。
• 每行的第一个整数大于前一行的最后一个整数。

示例 1：

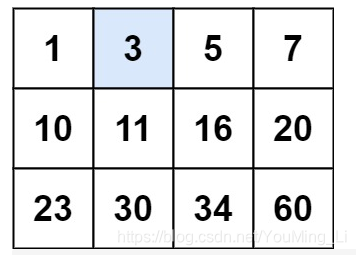
输入：matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3
输出：true

示例 2：

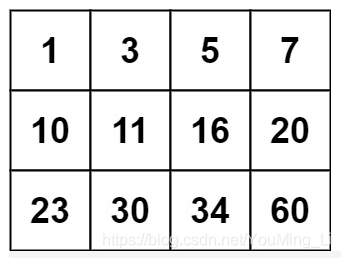
输入：matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13
输出：false

提示：

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 100
• -10^4 <= matrix[i][j], target <= 10^4

思路

我们不难发现题中的二维矩阵都是按Z字形递增的，故可以将二维的数组看成一个一维的递增数组，该一维数组的元素个数为n*m。

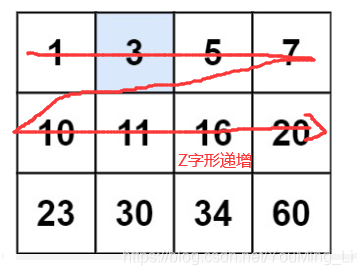
在0~n*m-1个数中，寻找大于等于target的最小值即可,最后找到的这个值如果等于target，说明找到了目标值，返回true。如果不等于，那就是大于，说明没有找到目标值，返回false即可。

Java代码

class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        if(matrix == null || matrix.length == 0 || matrix[0].length == 0)
            return false;
        int n = matrix.length;
        int m = matrix[0].length;
        //在0~n*m-1个数中,寻找大于等于target的最小值
        int l = 0,r = n*m - 1;
        while(l < r){
            int mid = l + r >> 1;
            //mid/m表示mid在二维数组中第几行，mid%m表示在第几列
            if(matrix[mid/m][mid%m] >= target) r = mid;
            else l = mid + 1;
        }
        if(matrix[l/m][l%m] == target) return true;
        return false;
    }
}

Go代码

符合条件的最大位置版本

func searchMatrix(matrix [][]int, target int) bool {
    // 由题意知：矩阵是z字形递增的，可以将其想象成一维递增数组处理
    // 用二分模板的寻找符合条件的最大位置  或者 符合条件的最小位置都可以做
    
    // 符合条件的最大位置版本
    if matrix == nil || len(matrix) == 0 || len(matrix[0]) == 0 {
        return false
    }
    row,col := len(matrix) ,len(matrix[0])
     //在0~n*m-1个数中,寻找大于等于target的最小值
    l,r := 0,  row * col - 1

    for l < r {
        mid := ( l + r + 1) / 2
        //mid/m表示mid在二维数组中第几行，mid%m表示在第几列
        if matrix[mid / col][mid % col] <= target  {
            l = mid
        } else {
            r = mid - 1
        }
    }

    if matrix[l / col][l % col] == target {
        return true
    }

    return false
}

符合条件的最小位置版本

func searchMatrix(matrix [][]int, target int) bool {
    // 由题意知：矩阵是z字形递增的，可以将其想象成一维递增数组处理
    // 用二分模板的寻找符合条件的最大位置  或者 符合条件的最小位置都可以做
    
    // 符合条件的最小位置版本
    if matrix == nil || len(matrix) == 0 || len(matrix[0]) == 0 {
        return false
    }
    row,col := len(matrix) ,len(matrix[0])
     //在0~n*m-1个数中,寻找大于等于target的最小值
    l,r := 0,  row * col - 1

    for l < r {
        mid := ( l + r) / 2
        //mid/m表示mid在二维数组中第几行，mid%m表示在第几列
        if matrix[mid / col][mid % col] >= target  {
            r = mid
        } else {
            l = mid + 1
        }
    }

    if matrix[l / col][l % col] == target {
        return true
    }

    return false
}

以右上角数字为基点的解法

func searchMatrix(matrix [][]int, target int) bool {
    if matrix == nil || len(matrix) == 0 || len(matrix[0]) == 0 {
        return false
    }
    // 右上角的数字大于对应行的所有数字，小于对应列的所有数字
    // 以右上角位置为基点，他比目标值大，则可以排除当前列，因为当前列肯定都比目标值大的
    // 他比目标值小，则可以排除当前行
    rows,cols := len(matrix) ,len(matrix[0])
    row ,col := 0,cols - 1
    
    for row <  rows && col < cols && col >= 0{
        if matrix[row][col] == target{
            return true
        } else if matrix[row][col] > target {
            col--
        } else {
            row++
        }
    }

    return false
}