数据结构之动态规划（四） | 零钱兑换python，matlab解法——力扣332经典例题

此节需要回顾前面的动态规划自底向上的计算方法和礼物问题，自底向上的计算办法是为了求出需要的硬币个数，后者是为了求出具体的硬币组合

零钱兑换

给定不同面值的硬币coins（理解成一个数组）和一个总金额s,编写一个函数来计算可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额返回-1,(每种硬币的数量是无限的, s以及coins中的元素都是正整数
假设我们要凑总金额为11，我们有1，2，5，20这四个面值的硬币，现在要求出最少需要的硬币个数和组合，我们不妨先画个图自己走一遍，可以发现可以发现1,5，5就是我们要求的，而10这一层向上就需要一个硬币即
F（11）=min(F（10）)+1 意思是面值为11的情况等于 面值为10的最少硬币组合+一个1块的硬币.
以此类推
F（10）=min(F（5）)+1 意思是面值为10的情况等于 面值为5的最少硬币组合+一个5块的硬币.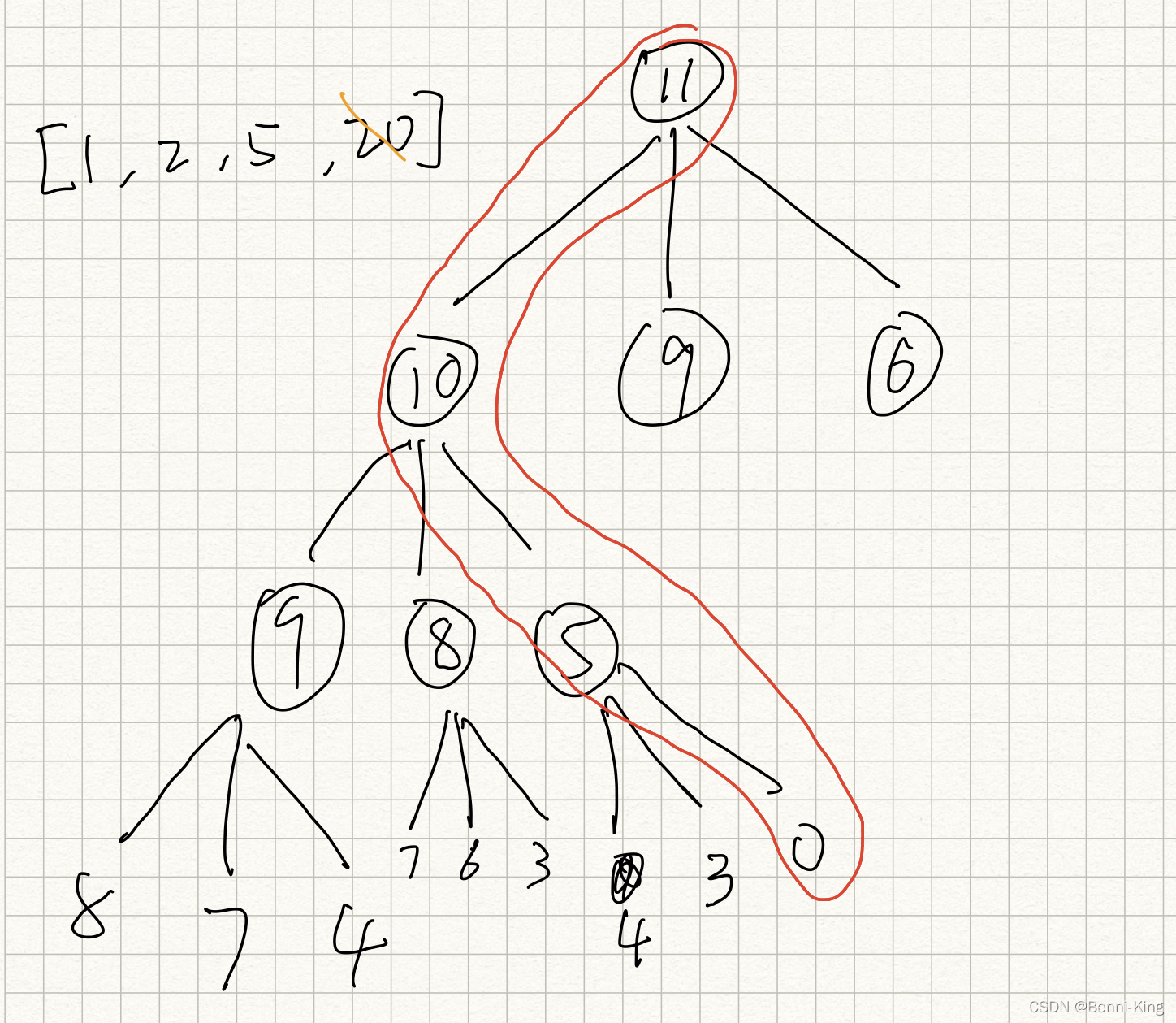
而这种至上而下的算法就是我们之前提到的迭代，十分耗费时间，所以我们采取至下而上的算法，从f（1）开始到f（11）

最后f（11）的个数就是3，就是最小硬币个数，

得出硬币组合

在我们这个表中, FF(11)-3,我们将3减去1得到2,然后在表格中找到: f(11-1),f(11-2),f(11-5)中哪一个是2,显然,f(10)=2.f(9)=3,f(6)=2,这里出现了两个2,说明可能出现了两个不同的方案,我们只需要选择任意一个就行,比如我们选择f(6),从x=6变成x=11需要一枚面值为5(11-6)的硬币,因此我们将5添加到IND中。(注意:在这一步的时候我们也可以直接判断f(10),f(9)和f(6)哪个最小,因为我们始终选择的是f(x-c)较小的那种情况

%% 怎么得到具体的硬币组合
function [f, IND] = coin_change2(coins, S)
    FF = +inf * ones(1,S+2);  
    FF(S+2) = 0;  % 最后一个元素改为0
    for x = 1:S
        tmp = x - coins;  
        tmp(tmp<0) = S+1;    
        tmp(tmp==0) = S+2;  
        FF(x) = min(FF(tmp))+1;
    end   
    % 利用FF来计算IND
    IND = [];  % IND表示我们选择的硬币组合，初始化为空向量
    
    if FF(S) < +inf  % 存在能凑成S的组合
        f = FF(S);
        ind = S;    % ind先指向最后一个位置S
        while FF(ind) > 1  % 如果FF(ind) = 1时就不用寻找了
            indd = ind;  % 保存前一个位置
            tmp = ind - coins;  
            tmp(tmp<0) = S+1;    % FF下标为S+1的元素为+inf
            tmp(tmp==0) = S+2;  % FF最后一个元素为0
            ind = tmp(find(FF(tmp) == (FF(ind) -1),1));  % 找到新的位置
            IND = [IND,indd-ind];  % 两个位置之差就是我们要添加的硬币
        end
        IND = [IND,ind];  % FF(ind) = 1时，把ind也放入到IND中
        
        
    else  % 如果没有任何一种硬币组合能组成总金额S就返回-1
        f = -1;   
    end
end

import numpy as np

class solution():
    ########定义你的硬币，和需要凑出来的总数S#######
    coins=[1,2,5,20]
    S=11
    #####################
    Coins=np.array(coins)
    FF = float("inf")*np.ones(S+2)
    FF[S+1] = 0
    
    #获取
    def get_num(self):
        for x in range(1,self.S+1):
            tmp = x-self.Coins
            tmp[tmp<0]=  self.S+1
            tmp[tmp==0]= self.S+2
            self.FF[x-1]=min(self.FF[tmp-1])+1
        
        if self.FF[self.S-1]< float("inf"):
            f = self.FF[self.S-1]
            return f
        else:
            return -1
    
    def get_combination(self,f):
        if f!=-1:
            ind = self.S
            IND=[]
            while self.FF[ind-1] >1:
                indd = ind
                tmp = ind - self.Coins
                tmp[tmp<0]=  self.S+1
                tmp[tmp==0]= self.S+2
                ind = 
                IND.append(indd-ind)
            IND.append(ind) #==1时的也加进去
            return IND
        else:
            return -1

leedcode322=solution()
f=leedcode322.get_num()
c=leedcode322.get_combination()
print(f)
print(c)