数据结构之动态规划（二）| 打家劫舍

自下而上（迭代）

创建一个矩阵，然后每次计算都返回这个矩阵，

function f= fib_dg_zxes(n)
    FF=ones(1,n);
    if n<=2
        f=1;
    else
        for i = 3:n
            FF(i)= FF(i-1)+FF(i-2);
        end
        f=FF(n);
    end
end

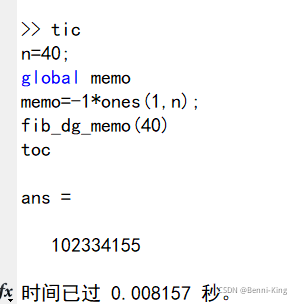
递归时间复杂度比较，这个是“备忘录形式”

这个是自下而上（迭代）的时间复杂度，可以看到呈四倍关系。

动态规划

多阶段决策问题中，各个阶段采取的决策，一般来说是与时间有关的，决策依赖于当前状态，又随即引起状态的转移，一个决策序列就是在变化的状态中产生出来的，故有“动态”的含义，称这种解决多阶段决策最优化问题的方法为动态规划方法

打家劫舍

你是一个专业的小偷，计划偷窃沿街的房屋。每间房内都藏有一定的现金，影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。
给定一个代表每个房屋存放金额的非负整数数组，计算你 不触动警报装置的情况下 ，一夜之内能够偷窃到的最高金额。

function f = djjs_dp(M)
    n = length(M);
    if n ==1
        f= M(1);
    elseif n==2
        f = max(M(1),M(2));
    else
        FF=ones(1,n);
        FF(1)=M(1);
        FF(2)=max(M(1),M(2));
        for i=3:n
            FF(i)=max(FF(i-1),(FF(i-2)+M(i)));
        end
        f=FF(n);
    end
end

这里也试了一下python，python递归的话就会很容易出现栈溢出的情况，还是有动态规划求解好，和matlab区别开来的是，list的索引是从0开始，matlab和SQL都是从1开始，所以要小改，创建矩阵的时候也用到了numpy。

import numpy as np
f=0

def djjs_dp(M) -> int :
    n=len(M)
    if n==1:
        f=M[0]
    elif n==2:
        f=max(M[0],M[1])
    else:
        FF=np.ones((1,n))
        FF=FF[0]
        FF[0]=M[0]
        FF[1]=max(M[0],M[1])
        for i in range(2,n):
            FF[i]=max(FF[i-1],(FF[i-2]+M[i]))
        f=FF[n-1]
    return f
M=[2,5,8,7,100,100]
djjs_dp(M)

下一期出第三期，背包问题和硬币问题，大家假期快乐