常微分方程Matlab数值解法-#1欧拉法

提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档

–

前言

常微分方程作为微分方程的基本类型之一，在自然界与工程界有很广泛的应用。很多问题的数学表述都可以归结为常微分方程的定解问题。

一、欧拉法（ Euler）

欧拉法（ Euler）是简单有效的常微分方程数值解法，欧拉法有多种形式的算法，其中简单欧
拉法是一种单步递推算

二、使用步骤

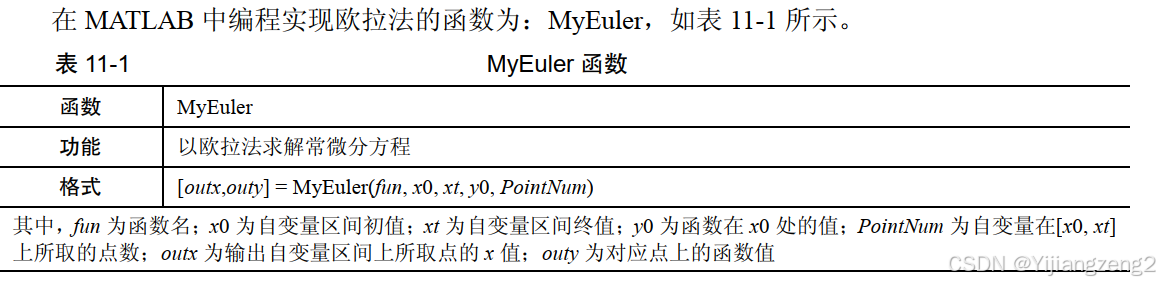
1.主函数

代码如下（示例）：
function [outx,outy]=MyEuler(fun,x0,xt,y0,PointNum)
%用前向差分的欧拉法解微分方程 y’=fun
%函数 f(x,y)： fun
%自变量的初值和终值： x0,xt
%y0 表示函数在 x0 处的值，输入初值为列向量形式
%自变量在[x0,xt]上取的点数： PointNum
%outx:所取的点的 x 值
%outy:对应点上的函数值
if nargin<5 | PointNum<=0 %如果函数仅输入 4 个参数值，则 PointNum 默认值为 100
PointNum=100;
end
if nargin<4 %y0 默认值为 0
y0=0;
end
h=(xt-x0)/PointNum; %计算步长 h
x=x0+[0:PointNum]'h; %自变量数组
y(1,:) = y0( : )‘; %输入存为列向量
for k = 1:PointNum
f=feval(fun,x(k),y(k,:)); %计算f(x,y)在每个迭代点的值
f=f( : )’;
y(k + 1, : ) =y(k, : ) +hf; %对于所取的点x,迭代计算y值
end
outy=y;
outx=x;
%plot(x,y) %画出方程解的函数图
end

2.实例分析

首先建立函数文件 myfun01.m：
function f=myfun01(x,y)
f=sin(x)+y;
end
通过在相同的积分区间上设定不同的取点数，从而改变步长，可得到不同的欧拉解。

% myfun01=sin(x)+y
clc
clear all
[x1,y1]=MyEuler(‘myfun01’,0,2pi,1,16); %欧拉法所得的解
h1=2pi/15 %计算取步长
[x11,y11]=MyEuler(‘myfun01’,0,2*pi,1,32); %欧拉法所得的解
h2=pi/15 %计算步长

y=dsolve(‘Dy=y+sin(t)’,‘y(0)=1’); %该常微分方程的符号解
for k=1:33
t(k)=x11(k);
y2(k)=subs(y,t(k)); %求其对应点的离散解
end
plot(x1,y1,‘+b’,x11,y11,‘og’,x11,y2,‘*r’)
legend(‘h=0.4 的欧拉解’,‘h=0.2 的欧拉解’,‘符号解’)

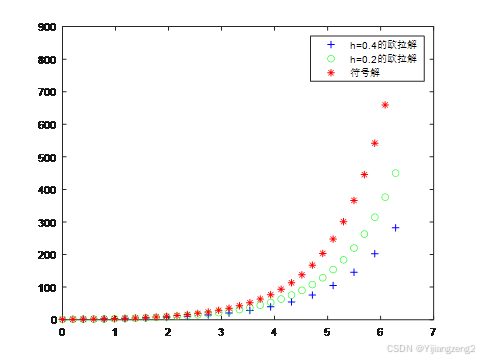
3.总结

用欧拉法得到的解和用符号法得到的解之间存在一定的误差，且取的步长越小，欧拉解越接近精确解。