zcy算法入门笔记003-树

YGFive

已于 2023-03-31 20:31:33 修改

阅读量129

点赞数

分类专栏： zcy入门课文章标签： java 数据结构

于 2023-03-21 08:15:56 首次发布

本文链接：https://blog.youkuaiyun.com/YiGeFive/article/details/129659872

版权

zcy入门课专栏收录该内容

4 篇文章

订阅专栏

本文介绍了几个关于二叉树的算法实现，包括判断两棵树是否相同、是否对称、计算最大和最小深度，以及如何构造二叉树和验证是否为平衡二叉搜索树。这些方法基于递归和树的遍历策略进行操作。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

相同的树

public static class TreeNode {
        public int val;
        public TreeNode left;
        public TreeNode right;
    }

    public static boolean isSameTree(TreeNode p, TreeNode q) {
        if (p == null ^ q == null) {
            //有一个为空，另一个不为空的话返回false
            return false;
        }
        if (p == null && q == null) {
            //空树=空树
            return true;
        }
        // 都不为空：1.头结点的值相等 2.左树同一个结构 3.右树同一个结构
        return p.val == q.val && isSameTree(p.left, q.left) && isSameTree(p.right, q.right);
    }

对称二叉树

public static class TreeNode {
        public int val;
        public TreeNode left;
        public TreeNode right;
    }

    public static boolean isSymmetric(TreeNode root) {
        return isMirror(root, root);
    }

    public static boolean isMirror(TreeNode h1, TreeNode h2) {
        if (h1 == null ^ h2 == null) {
            //一个为空、一个不为空则直接false
            return false;
        }
        if (h1 == null && h2 == null) {
            //空树和空树是镜面关系
            return true;
        }
        //镜面：1.节点值相等 2.我的左树和你的右树是镜面 3.我的右树和你的左树是镜面
        return h1.val == h2.val && isMirror(h1.left, h2.right) && isMirror(h1.right, h2.left);
    }

二叉树的最大深度

public static class TreeNode {
        public int val;
        public TreeNode left;
        public TreeNode right;
    }

    // 以root为头的树，最大高度是多少返回！
    public static int maxDepth(TreeNode root) {
        if (root == null) {
            return 0;
        }
        return Math.max(maxDepth(root.left), maxDepth(root.right)) + 1;
    }

二叉树的最小深度

public static class TreeNode {
        public int val;
        public TreeNode left;
        public TreeNode right;
    }
// 以root为头的树，最小高度是多少返回！
    public static int minDepth(TreeNode root){
        if(root==null){
            return 0;
        }
        /**
         * 叶子节点的定义是左孩子和右孩子都为 null 时叫做叶子节点
         * 1.如果root节点左右子树都为空，返回0
         * 2.如果root节点左右子树有一个为空，返回不空子树的深度
         * 3.如果root节点左右子树都不为空，返回左右子树较小的深度
         */
        int m1 = minDepth(root.left);
        int m2 = minDepth(root.right);
        //1.如果左右孩子有空的情况，返回m1+m2+1
        //2.如果左右孩子都不为空，返回较小深度+1
        return root.left==null || root.right == null ? m1+m2+1 : Math.min(m1, m2)+1;
    }

平衡二叉树

public static class TreeNode {
        public int val;
        public TreeNode left;
        public TreeNode right;

        TreeNode(int val) {
            this.val = val;
        }
    }

    public static boolean isBalanced(TreeNode root) {
        return process(root).isBalanced;
    }

    //假设以某个节点为头的时候    1)整棵树是否平   2)整棵树的高度是什么
    public static class Info {
        public boolean isBalanced;  //是否平衡
        public int height;  //高度

        public Info(boolean i, int h) {
            isBalanced = i;
            height = h;
        }
    }
    public static Info process(TreeNode root) {
        if (root == null) {     //空树是平衡树、高度0
            return new Info(true, 0);
        }
        //不为空时，去左右子树收集信息
        Info leftInfo = process(root.left);
        Info rightInfo = process(root.right);
        //高度为左右子树最大值+1
        int height = Math.max(leftInfo.height, rightInfo.height) + 1;
        //要求左树整体平衡、右树整体平衡、左右子树高度差的绝对值<2
        boolean isBalanced = leftInfo.isBalanced && rightInfo.isBalanced
                && Math.abs(leftInfo.height - rightInfo.height) < 2;
        return new Info(isBalanced, height);
    }

从前序与中序遍历序列构造二叉树

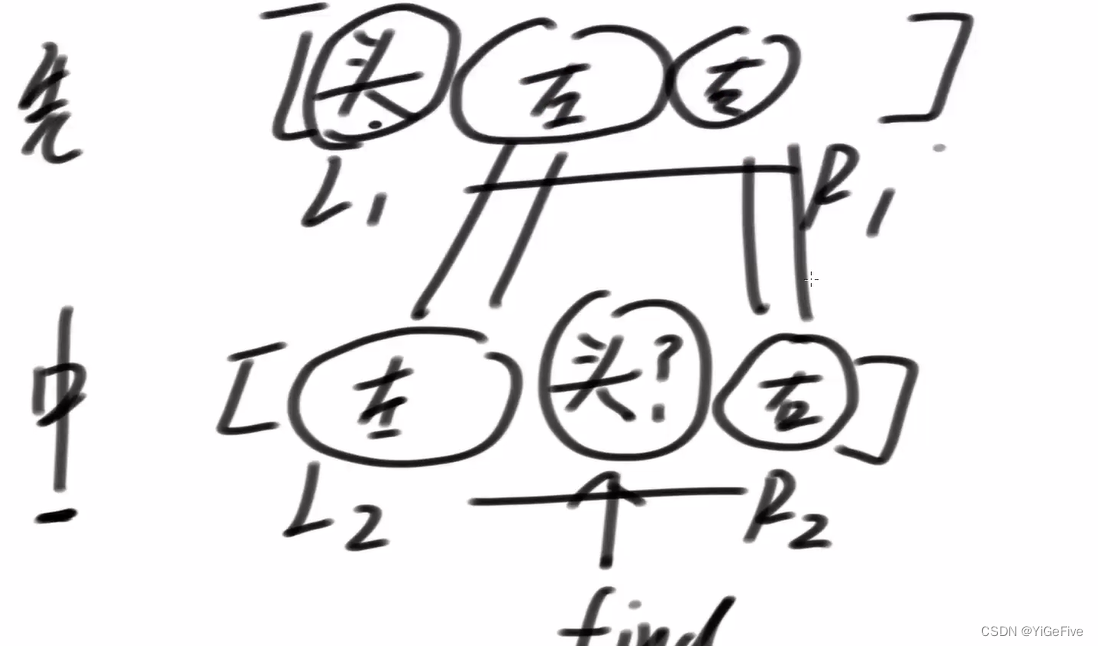
特殊判断：L1>R1

情况：出现越界，说明这时候是空树，应该返回null

代码

import java.util.HashMap;

//测试链接：https://leetcode.com/problems/construct-binary-tree-from-preorder-and-inorder-traversal
public class Code05_ConstructBinaryTreeFromPreorderAndInorderTraversal {
    /*
        用先序数组和中序数组重建一棵树
    */
    public static class TreeNode {
        int val;
        TreeNode left;
        TreeNode right;

        TreeNode(int val) {
            this.val = val;
        }
    }

    public static TreeNode buildTree1(int[] pre, int[] in) {
        if (pre == null || in == null || pre.length != in.length) {
            return null;
        }
        return f(pre, 0, pre.length - 1, in, 0, in.length - 1);
    }

    // 有一棵树，先序结果是pre[L1...R1]，中序结果是in[L2...R2]
    // 请建出整棵树返回头节点
    public static TreeNode f(int[] pre, int L1, int R1, int[] in, int L2, int R2) {
        if (L1 > R1) {  //控制范围
            return null;
        }
        TreeNode head = new TreeNode(pre[L1]);
        if (L1 == R1) {     //只有一个节点
            return head;
        }
        int find = L2;
        while (in[find] != pre[L1]) {   //通过遍历寻找头结点，可以优化
            find++;
        }
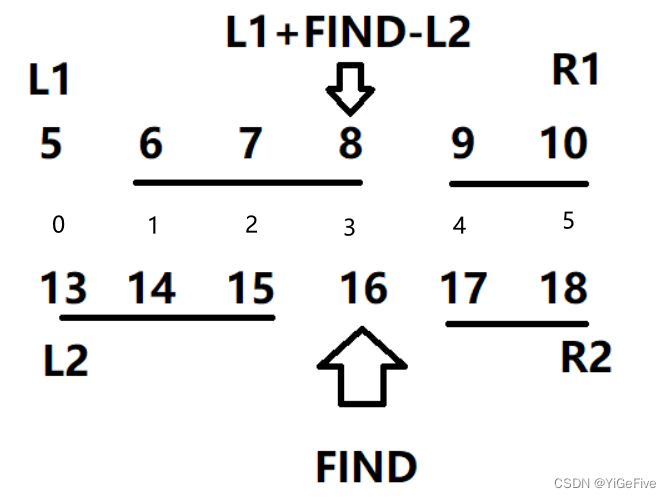
        head.left = f(pre, L1 + 1, L1 + find - L2, in, L2, find - 1);
        head.right = f(pre, L1 + find - L2 + 1, R1, in, find + 1, R2);
        return head;
    }

    public static TreeNode buildTree2(int[] pre, int[] in) {
        if (pre == null || in == null || pre.length != in.length) {
            return null;
        }
        //空间换时间的优化：在整个过程开始前把中序数组每一个值在哪记到表中，直接从表中查下标，省去遍历
        HashMap<Integer, Integer> valueIndexMap = new HashMap<>();
        for (int i = 0; i < in.length; i++) {
            valueIndexMap.put(in[i], i);
        }
        return g(pre, 0, pre.length - 1, in, 0, in.length - 1, valueIndexMap);
    }

    // 有一棵树，先序结果是pre[L1...R1]，中序结果是in[L2...R2]
    // 请建出整棵树返回头节点
    public static TreeNode g(int[] pre, int L1, int R1, int[] in, int L2, int R2,
                             HashMap<Integer, Integer> valueIndexMap) {
        if (L1 > R1) {
            return null;
        }
        TreeNode head = new TreeNode(pre[L1]);
        if (L1 == R1) {
            return head;
        }
        int find = valueIndexMap.get(pre[L1]);  //省去遍历 直接查表
        head.left = g(pre, L1 + 1, L1 + find - L2, in, L2, find - 1, valueIndexMap);
        head.right = g(pre, L1 + find - L2 + 1, R1, in, find + 1, R2, valueIndexMap);
        return head;
    }

}

二叉树的层序遍历 II

思路：头节点先加入队列，依据此时队列长度然后依次弹出节点，此时出队节点有左孩子，则左孩子先加入队列，节点有右孩子，则右孩子加入队列，每趟循环弹出一层节点用链表结构收集起来。

代码

import java.util.LinkedList;
import java.util.List;
import java.util.Queue;

// 测试链接：https://leetcode.com/problems/binary-tree-level-order-traversal-ii
public class Code01_BinaryTreeLevelOrderTraversalII {

    public static class TreeNode {
        public int val;
        public TreeNode left;
        public TreeNode right;

        TreeNode(int val) {
            this.val = val;
        }
    }
    /**
     *  二叉树的层序遍历 II
     */
    public List<List<Integer>> levelOrderBottom(TreeNode root) {
        List<List<Integer>> ans = new LinkedList<>();
        if (root == null) {
            return ans;
        }
        Queue<TreeNode> queue = new LinkedList<>();
        queue.add(root);
        while (!queue.isEmpty()) {
            int size = queue.size();
            List<Integer> curAns = new LinkedList<>();
            for (int i = 0; i < size; i++) {
                TreeNode curNode = queue.poll();
                curAns.add(curNode.val);
                if (curNode.left != null) {
                    queue.add(curNode.left);
                }
                if (curNode.right != null) {
                    queue.add(curNode.right);
                }
            }
            ans.add(0, curAns);
        }
        return ans;
    }

}

验证二叉搜索树

public static class TreeNode {
        public int val;
        public TreeNode left;
        public TreeNode right;

        TreeNode(int val) {
            this.val = val;
        }
    }

    public static class Info {
        // 递归：对所有节点一视同仁，信息要同等全，每个节点返回三个信息
        public boolean isBST;   //1.整体是否是搜索二叉树
        public int max;         //2.整棵树最大值
        public int min;         //3.整棵树最小值

        public Info(boolean is, int ma, int mi) {
            isBST = is;
            max = ma;
            min = mi;
        }
    }

//    public static Info process(TreeNode x) {
//        if (x == null) {    //考虑单个负节点情况，空的情况：不能设最大值、最小值为0
        //在判空时返回空信息，要把判空的任务交给上游去判断
//            return null;
//        }
    //先向左、右树去收集信息：可能都空、都不空、其中一个空
//        Info leftInfo = process(x.left);
//        Info rightInfo = process(x.right);
//        int max = x.val;
//        int min = x.val;
    //子树不为空时，有可能比我节点的max大，min小
//        if (leftInfo != null) {
//            max = Math.max(leftInfo.max, max);
//            min = Math.min(leftInfo.min, min);
//        }
//        if (rightInfo != null) {
//            max = Math.max(rightInfo.max, max);
//            min = Math.min(rightInfo.min, min);
//        }
    //先认为是搜索二叉树
//        boolean isBST = true;
    //左树不为空且左树已经不是搜索二叉树了
//        if (leftInfo != null && !leftInfo.isBST) {
//            isBST = false;
//        }
    //右树不为空且右树已经不是搜索二叉树了
//        if (rightInfo != null && !rightInfo.isBST) {
//            isBST = false;
//        }
        // left max < x?   right min > x?
        // 左树空时默认左树max<x,不空时实际去判断一下max是否<x，右树同理
//        boolean leftMaxLessX = leftInfo == null ? true : (leftInfo.max < x.val);
//        boolean rightMinMoreX = rightInfo == null ? true : (rightInfo.min > x.val);
//        if (!(leftMaxLessX && rightMinMoreX)) {
//            isBST = false;
//        }
//        return new Info(isBST, max, min);
//    }