BP神经网络学习

一、概述

BP(back propagation)神经网络是1986年由Rumelhart和McClelland为首的科学家提出的概念，是一种按照误差逆向传播算法训练的多层前馈神经网络，是目前应用最广泛的神经网络。

二、训练过程

网络结构：前馈过程
1、设网络输入为x，则隐含层第j个结点的输入为：

网络输出层第k个结点的输入为：

因此，网络输出层第k个结点的输出为：


2、训练过程
假设N个样本在网络中的总误差为：

其中 表示第n个样本对应标签的第k维， 表示第n个样本在网络输
出的第k维。在多类分类问题中，输出一般组织为“one-of-c”的形式。
如果考虑随机梯度下降，则单个样本的误差为：

网络学习的目的是根据训练数据的误差E对于各个参数的梯度，求解
参数调整量：

其中输出层权重调整量：

输出层阈值调整：


回顾E, netk, yk的定义

可得：

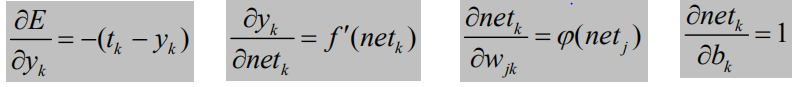
代入参数调整量，可得：

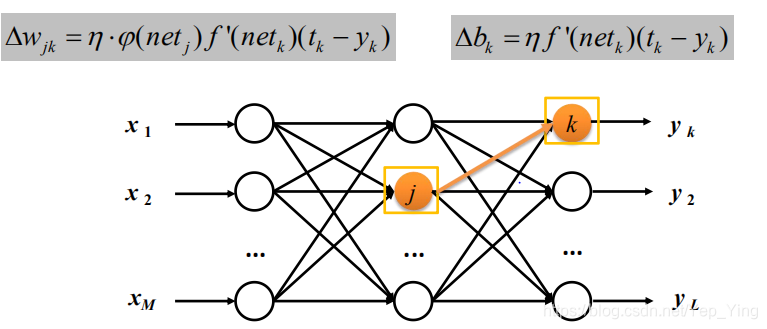
f 以Sigmoid激活函数为例

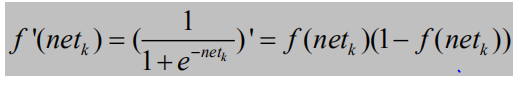
以权值调整更新为例：


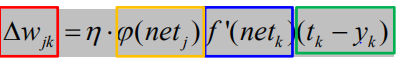
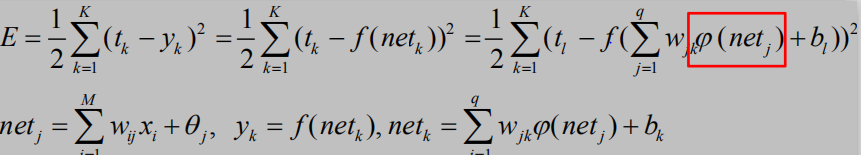
网络学习的目的是根据训练数据的误差E对于各个参数的梯度，求解
参数调整量：

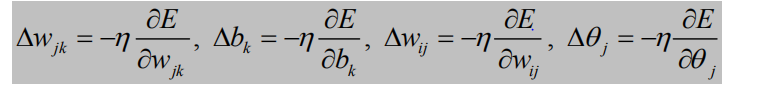
其中隐含层权重调整量：

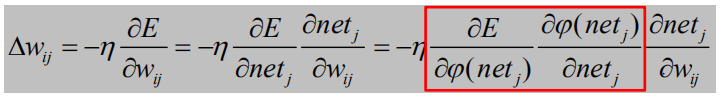
隐含层阈值调整：


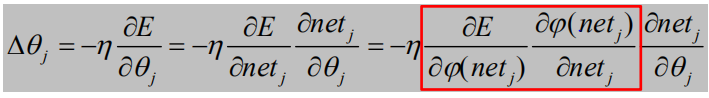
将上述公式代入隐含层参数调整量，可得：

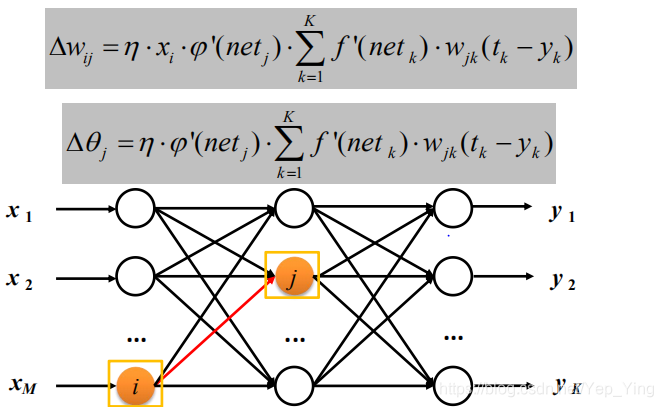
φ 以Sigmoid激活函数为例

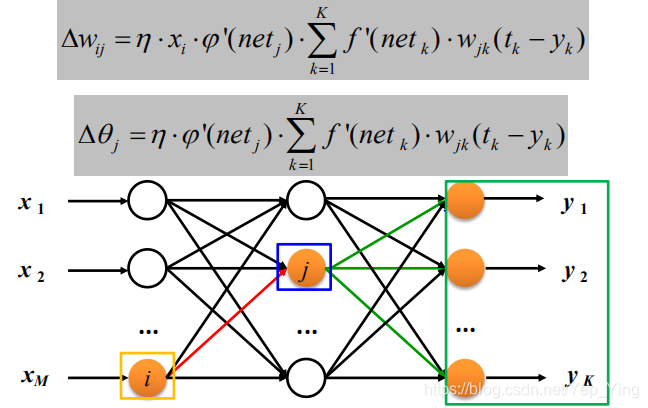
以权值调整更新为例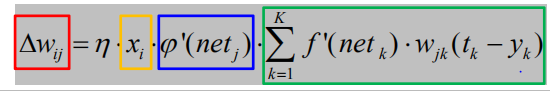
在多层网络中，为了方便误差反传推导，Rumelhart提出了误差信号（误差灵敏度）
的概念。其中输出层误差信号为：

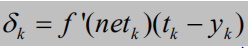
隐含层误差信号为：

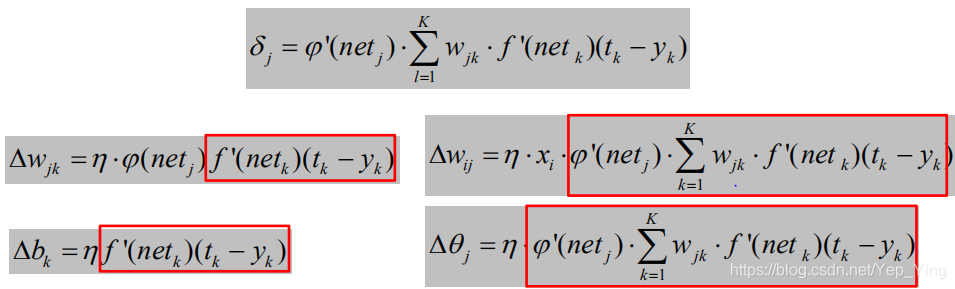
于是对于每一层的权重矩阵W和偏置向量B的参数更新量为：

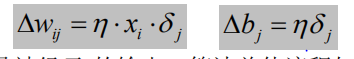
其中xj是神经元j的输出，算法总体流程如下：
输入：网络结构参数（层数、结点数等）；训练数据集
输出：网络权值与阈值

1. 网络权值初始化；
2. 对输入训练S={(x1, t1), (x2, t2), …, (xK, tK)}，依次通过输
   入层、隐含层、输出层，并分别计算误差E；
3. 通过误差E反传计算每个神经元的误差信号δ；
4. 根据误差信号δ调整网络权值W和结点阈值θ；
5. 对训练数据不断滚动(Epoch)，直至最大滚动次数或误
   差低于某一阈值为止。
   PS：训练过程可采用随机梯度下降，或批量梯度下降方法。

三、代码实现与结果

% BP网络
% BP神经网络的构建
net=newff([-1 2;0 5],[3,1],{'tansig','purelin'},'traingd')
net.IW{1}
net.b{1}

p=[1;2];
a=sim(net,p)
net=init(net);
net.IW{1}
net.b{1}
a=sim(net,p)
%net.IW{1}*p+net.b{1}
p2=net.IW{1}*p+net.b{1}
a2=sign(p2)
a3=tansig(a2)
a4=purelin(a3)
net.b{2}
net.b{1}

net.IW{1}
net.IW{2}
0.7616+net.b{2}
a-net.b{2}
(a-net.b{2})/ 0.7616
help purelin

p1=[0;0];
a5=sim(net,p1)
net.b{2}
% BP网络
% BP神经网络的构建
net=newff([-1 2;0 5],[3,1],{'tansig','purelin'},'traingd')
net.IW{1}
net.b{1}
%p=[1;];
p=[1;2];
a=sim(net,p)
net=init(net);
net.IW{1}
net.b{1}
a=sim(net,p)
net.IW{1}*p+net.b{1}
p2=net.IW{1}*p+net.b{1}
a2=sign(p2)
a3=tansig(a2)
a4=purelin(a3)
net.b{2}
net.b{1}




P=[1.2;3;0.5;1.6]
W=[0.3 0.6 0.1 0.8]
net1=newp([0 2;0 2;0 2;0 2],1,'purelin');
net2=newp([0 2;0 2;0 2;0 2],1,'logsig');
net3=newp([0 2;0 2;0 2;0 2],1,'tansig');
net4=newp([0 2;0 2;0 2;0 2],1,'hardlim');

net1.IW{1}
net2.IW{1}
net3.IW{1}
net4.IW{1}
net1.b{1}
net2.b{1}
net3.b{1}
net4.b{1}


net1.IW{1}=W;
net2.IW{1}=W;
net3.IW{1}=W;
net4.IW{1}=W;

a1=sim(net1,P)
a2=sim(net2,P)
a3=sim(net3,P)
a4=sim(net4,P)

init(net1);
net1.b{1}

help tansig

% 训练
p=[-0.1 0.5]
t=[-0.3 0.4]
w_range=-2:0.4:2;
b_range=-2:0.4:2;

ES=errsurf(p,t,w_range,b_range,'logsig');%单输入神经元的误差曲面
plotes(w_range,b_range,ES)%绘制单输入神经元的误差曲面
pause(0.5);
hold off;
net=newp([-2,2],1,'logsig');
net.trainparam.epochs=100;
net.trainparam.goal=0.001;
figure(2);
[net,tr]=train(net,p,t);
title('动态逼近')
wight=net.iw{1}
bias=net.b
pause;
close;
% 练
p=[-0.2 0.2 0.3 0.4]
t=[-0.9 -0.2 1.2 2.0]
h1=figure(1);
net=newff([-2,2],[5,1],{'tansig','purelin'},'trainlm');
net.trainparam.epochs=100;
net.trainparam.goal=0.0001;
net=train(net,p,t);
a1=sim(net,p)
pause;
h2=figure(2);
plot(p,t,'*');
title('样本')
title('样本');
xlabel('Input');
ylabel('Output');
pause;
hold on;
ptest1=[0.2 0.1]
ptest2=[0.2 0.1 0.9]
a1=sim(net,ptest1);
a2=sim(net,ptest2);

net.iw{1}
net.iw{2}
net.b{1}
net.b{2}

运行结果


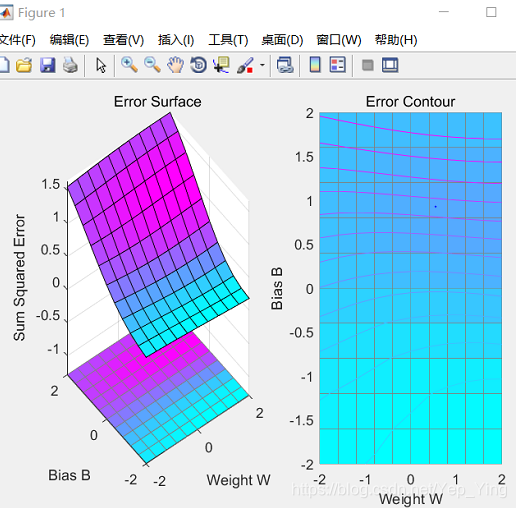
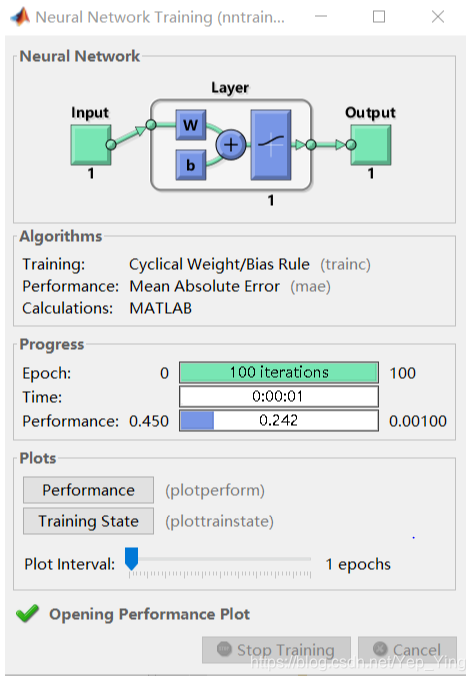
样本绘图结果


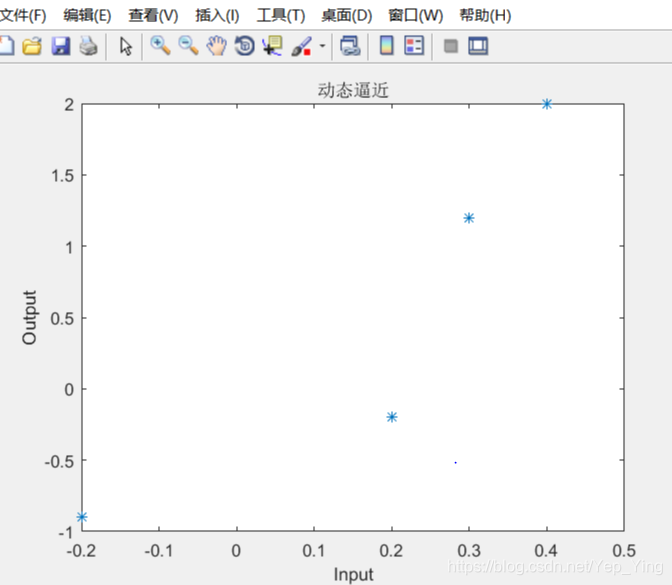
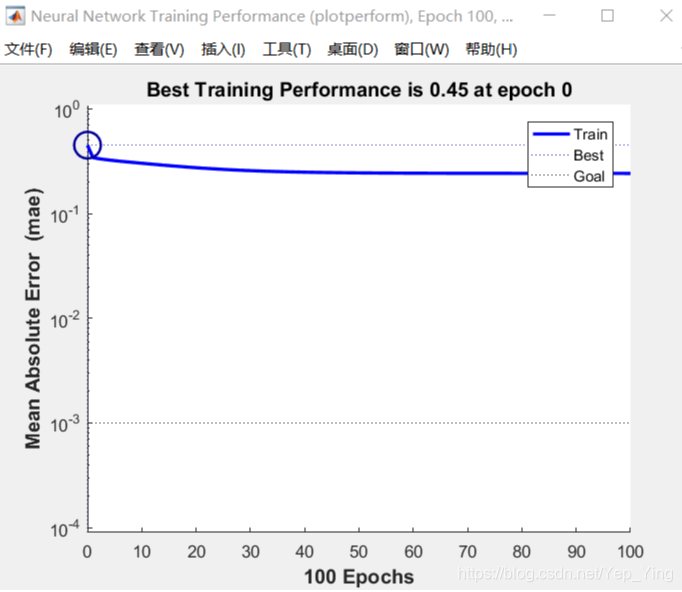
BP神经网络性能图

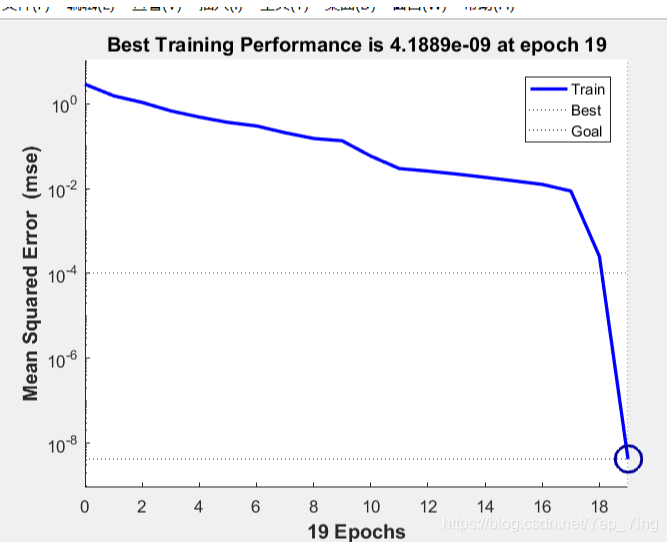
训练状态图

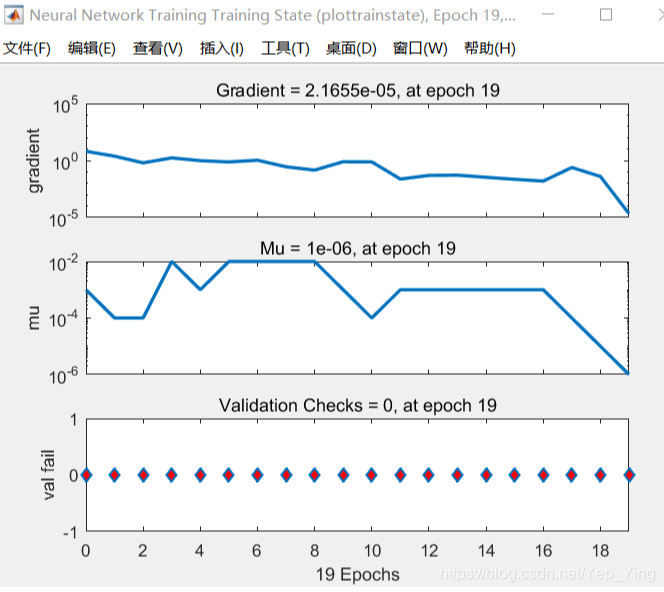
回归分析结果图

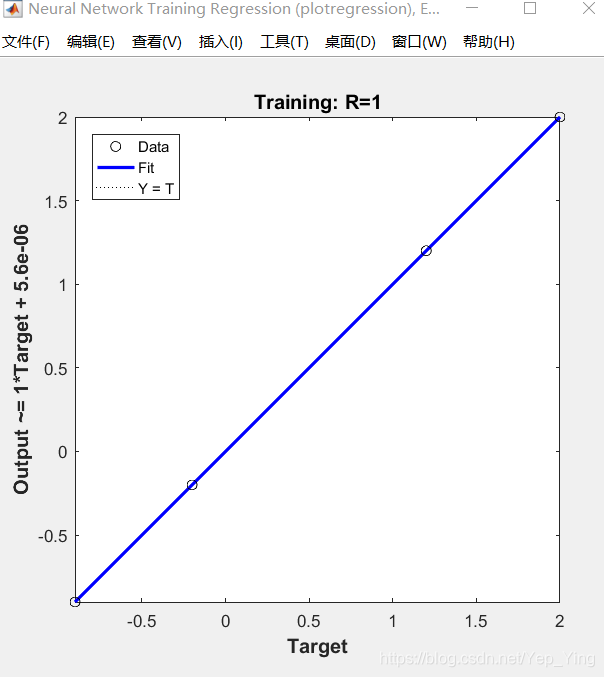
四、代码解释

1.newff函数
newff函数的格式为：
net=newff(PR,[S1 S2 …SN],{TF1 TF2…TFN},BTF,BLF,PF），函数newff建立一个可训练的前馈网络。输入参数说明：
PR：Rx2的矩阵以定义R个输入向量的最小值和最大值；
Si：第i层神经元个数；
TFi：第i层的传递函数，默认函数为tansig函数；
BTF：训练函数，默认函数为trainlm函数；
BLF：权值/阈值学习函数，默认函数为learngdm函数；
PF：性能函数，默认函数为mse函数。
2.learnp函数
句法：
[dW，LS] = learnp（W，P，Z，N，A，T，E，gW，gA，D，LP，LS）
info = learnp（‘code’）
描述：
learnp是感知器重量/偏差学习功能。

[dW，LS] = learnp（W，P，Z，N，A，T，E，gW，gA，D，LP，LS）需要几个输入，

W - SxR权重矩阵（或b，Sx1偏差向量）。
P - RxQ输入向量（或（1，Q））。
Z - SxQ加权输入向量。
N - SxQnet输入向量。
A - SxQ输出向量。
T - SxQ层目标向量。
E - SxQ层误差向量。
gW - 相对于性能的SxR梯度。
gA - SxQ输出梯度与性能有关。
D - SxS神经元距离。
LP - 学习参数，无，LP = []。
LS - 学习状态，最初应为= []。
并返回，
dW - SxR权重（或偏差）改变矩阵。
LS - 新的学习状态。

五、优点与缺点

BP网络优点：
1.具有非线性映射能力，理论上可以无限逼近任意复杂函数；
2. 网络结构简单，计算复杂度低；
3. 具有较好的容错能力，网络结构部分受损不会对结果产生很大的影响；
BP网络问题：
1.样本依赖性强，比较容易过拟合；
2. 误差反传有水波现象(gradient diffusion（梯度扩散）)，梯度越来越从顶层越往下，误差校正信号越来越小。
3. 网络结构和初始参数对结果影响很大，容易收敛到局部最小值；
4. 训练速度比较慢，效率相比SVM和boosting没有优势；