计算视差图

一、计算视差原理

1.1立体图像

一个多视图成像的特殊例子是立体视觉(或者立体成像)，即使用两台只有水平(向一侧)偏移的照相机观测同-.场景。当照相机的位置如上设置，两幅图像具有相同的图像平面，图像的行是垂直对齐的，那么称图像对是经过矫正的。该设置在机器人学中很常见，常被称为立体平台。通过将图像扭曲到公共的平面，上，使外极线位于图像行上，任何立体照相机设置都能得到矫正(我们通常构建立体平台来产生经过矫正的图像对)。假设两幅图像经过了矫正，那么对应点的寻找限制在图像的同一行.上。一旦找到对应点，由于深度是和偏移成正比的，那么深度(Z坐标)可以直接由水平偏移来计算,

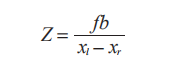
其中，f是经过矫正图像的焦距，b是两个照相机中心之间的距离，x和x,是左右两.幅图像中对应点的x坐标。分开照相机中心的距离称为基线。矫正后的立体照相机设置如图所示。

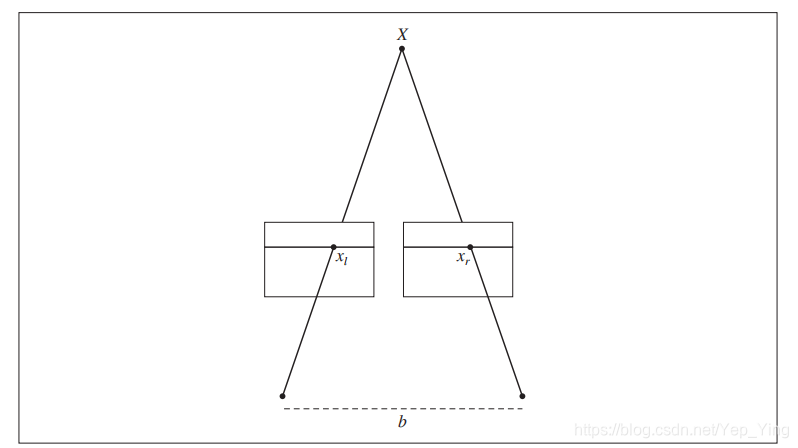
立体重建(有时称为致密深度重建)就是恢复深度图(或者相反，视差图)，图像中.每个像素的深度(或者视差)都需要计算出来。

1.2计算视图差

当密集地应用在图像中时，归一化的互相关值可以很快地计算出来。我们使用每个像素周围的图像块(根本上说，是局部周边图像)来计算归一化的互相关。对于这里的情形，我们可以在像素周围写出公式中的NCC,如下所示

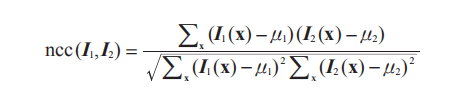
1.3双目立体匹配

1、采集图像：通过标定好的双目相机采集图像，可以用两个单目相机来组合成双目相机。
2、极线校正：校正的目的是使两帧图像极线处于水平方向，或者说是使两帧图像的光心处于同一水平线上。通过校正极线可以方便后续的NCC操作。
3、特征匹配：匹配方法如上所述，右视图中与左视图待测像素同一水平线上相关性最高的即为最优匹配。完成匹配后，我们需要记录其视差d，即待测像素水平方向xl与匹配像素水平方向xr之间的差值d = xr - xl，最终我们可以得到一个与原始图像尺寸相同的视差图D。
4、深度恢复：通过上述匹配结果得到的视差图D，我们可以很简单的利用相似三角形反推出以左视图为参考系的深度图。

二、代码实现

2.1图片集

左相机

右相机

2.2结果展示

窗口值wid=4时

窗口值wid=6时

窗口值wid=9时

窗口值wid=12时

2.3代码

# -*- coding: utf-8 -*-
from PIL import Image
from pylab import *
import cv2
from numpy import *
from numpy.ma import array
from scipy.ndimage import filters
def plane_sweep_ncc(im_l,im_r,start,steps,wid):
    """ 使用归一化的互相关计算视差图像 """
    m,n = im_l.shape
    # 保存不同求和值的数组
    mean_l = zeros((m,n))
    mean_r = zeros((m,n))
    s = zeros((m,n))
    s_l = zeros((m,n))
    s_r = zeros((m,n))
    # 保存深度平面的数组
    dmaps = zeros((m,n,steps))
    # 计算图像块的平均值
    filters.uniform_filter(im_l,wid,mean_l)
    filters.uniform_filter(im_r,wid,mean_r)
    # 归一化图像
    norm_l = im_l - mean_l
    norm_r = im_r - mean_r
    # 尝试不同的视差
    for displ in range(steps):
        # 将左边图像移动到右边，计算加和
        filters.uniform_filter(np.roll(norm_l, -displ - start) * norm_r, wid, s) # 和归一化
        filters.uniform_filter(np.roll(norm_l, -displ - start) * np.roll(norm_l, -displ - start), wid, s_l)
        filters.uniform_filter(norm_r*norm_r,wid,s_r) # 和反归一化
        # 保存 ncc 的分数
        dmaps[:,:,displ] = s / sqrt(s_l * s_r)
        # 为每个像素选取最佳深度
    return np.argmax(dmaps, axis=2)

def plane_sweep_gauss(im_l,im_r,start,steps,wid):
 """ 使用带有高斯加权周边的归一化互相关计算视差图像 """
 m,n = im_l.shape
 # 保存不同加和的数组
 mean_l = zeros((m,n))
 mean_r = zeros((m,n))
 s = zeros((m,n))
 s_l = zeros((m,n))
 s_r = zeros((m,n))
 # 保存深度平面的数组
 dmaps = zeros((m,n,steps))
 # 计算平均值
 filters.gaussian_filter(im_l,wid,0,mean_l)
 filters.gaussian_filter(im_r,wid,0,mean_r)
 # 归一化图像
 norm_l = im_l - mean_l
 norm_r = im_r - mean_r
 # 尝试不同的视差
 for displ in range(steps):
     # 将左边图像移动到右边，计算加和
     filters.gaussian_filter(np.roll(norm_l, -displ - start) * norm_r, wid, 0, s) # 和归一化
     filters.gaussian_filter(np.roll(norm_l, -displ - start) * np.roll(norm_l, -displ - start), wid, 0, s_l)
     filters.gaussian_filter(norm_r*norm_r,wid,0,s_r) # 和反归一化
     # 保存 ncc 的分数
     dmaps[:,:,displ] = s / np.sqrt(s_l * s_r)
 # 为每个像素选取最佳深度
 return np.argmax(dmaps, axis=2)

im_l = array(Image.open('1.png').convert('L'), 'f')
im_r = array(Image.open('2.png').convert('L'),'f')
# 开始偏移，并设置步长
steps = 12
start = 4
# ncc 的宽度
wid = 9
res = plane_sweep_ncc(im_l,im_r,start,steps,wid)
import scipy.misc
scipy.misc.imsave('depth.png',res)
show()

三、实验结果分析

当窗口值改变时，结果也跟着改变。窗口值越大，匹配结果区分度越高，但也不能太大，窗口值太大时，匹配结果容易变得很黑。窗口值小时，容易出现颗粒状，图片辨认度低。