哈夫曼树(Huffman Tree)
定义
- 带权路径长度(WPL):设二叉树有n个叶子结点,每个叶子结点带有权值wk,从根结点到每个叶子结点的长度为lk,则每个叶子结点的带权路径长度之和为:WPL=∑nk=1wklk
- 最优二叉树或哈夫曼树:WPL最小的二叉树
哈夫曼树的构造
假设有n个权值结点,则构造出的哈夫曼树有n个叶子结点:
- 将w1,w2,...,wn看成是有n棵树的森林(每棵树仅有一个结点)
- 在森林中选出两个根结点的权值最小的树合并,作为一棵新树的左右子树,且新树的根结点权值为其左、右子树根结点权值之和
- 从森林中删除选取的两棵树,并将新树加入森林
- 重复2、3步,直到森林中只剩一棵树为止,该树即为所求的哈夫曼树
实现
算法:
- 将所有的权值结点构造一个最小堆
- 重复Size−1次合并操作:
- 构建一个新结点
- 该结点的左右子结点为最小堆的堆顶元素
- 该结点的权值为左右子结点权值之和
- 插入到最小堆中
- 此时堆顶的结点为哈夫曼树的根结点
typedef struct TreeNode *HuffmanTree;
struct TreeNode {
int Weight;
HuffmanTree Left, Right;
}
HuffmanTree Huffman(MinHeap H) {
// 假设H->Size个权值已经存在H->Elements[]->Weight里
int i;
HuffmanTree T;
BuildMinHeap(H); // 将H->Elements[]按权值调整为最小堆
for (int i = 1; i < H->Size; i++) { // 做H->Size-1次合并
T = malloc(sizeof(struct TreeNode)); // 建立新结点
T->Left = DeleteMin(H); // 从最小堆中删除一个结点,作为新T的左子结点
T->Right = DeleteMin(H); // 从最小堆中删除一个结点,作为新T的右子结点
T->Weight = T->Left->Weight + T->Right->Weight; // 计算新权值
Insert(H, T); // 将新T插入最小堆
}
T = DeleteMin(H);
return T;
}时间复杂度:O(NlogN)
哈夫曼树的特点
- 没有度为1的结点
- n个叶子结点的哈夫曼树共有2n−1个结点
- 哈夫曼树的任意非叶结点的左右子树交换后仍是哈夫曼树
- 对同一组权值{w1,w2,...,wn} `,存在不同构的两棵哈夫曼树
- 例,对一组权值{1,2,3,3} ,不同构的两棵哈夫曼树:
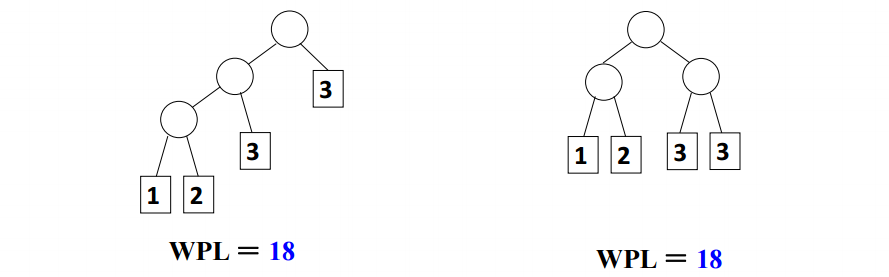








 本文详细介绍了哈夫曼树的基本概念、构造方法及特点。哈夫曼树是一种特殊的二叉树,通过确保带权路径长度最小来优化数据结构。文章还提供了哈夫曼树的实现算法及代码示例。
本文详细介绍了哈夫曼树的基本概念、构造方法及特点。哈夫曼树是一种特殊的二叉树,通过确保带权路径长度最小来优化数据结构。文章还提供了哈夫曼树的实现算法及代码示例。
















 428
428

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








