红黑树(RBT)

总览：

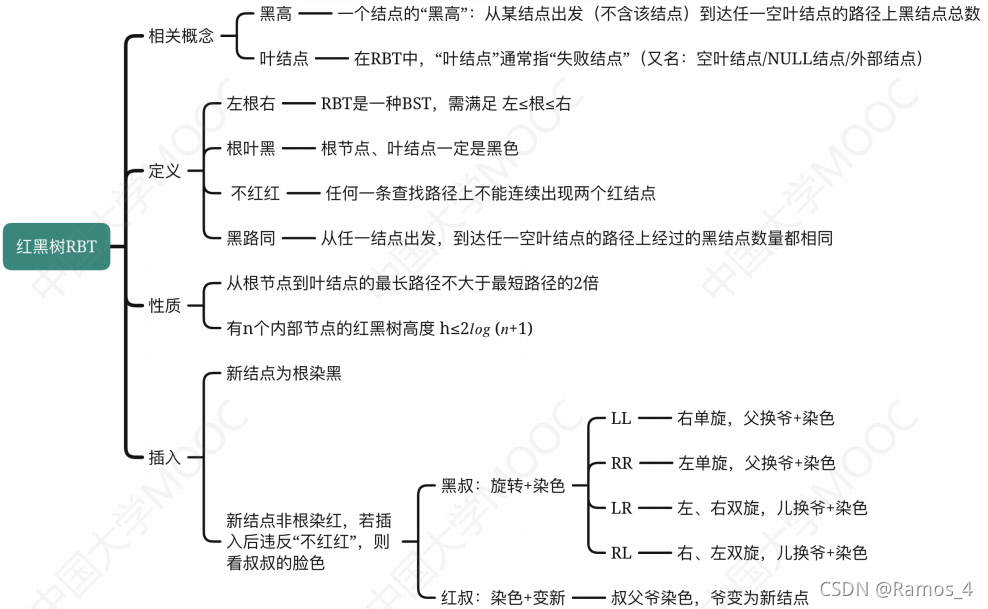
一、红黑树的相关概念

RBT就是二叉排序树（BST）的一种优化

具体定义：

红黑树是二叉排序树→左子树结点值 ≤ 根结点值 ≤ 右子树结点值

与普通BST相比，有如下要求：

①每个结点或是红色，或是黑色的
②根节点是黑色的
③叶结点（外部结点、NULL结点、失败结点）均是黑色的
④不存在两个相邻的红结点（即红结点的父节点和孩子结点均是黑色）
⑤对每个结点，从该节点到任一叶结点的简单路径上，所含黑结点的数目相同

简记：左根右，根叶黑，不红红，黑路同

 性质：

 代码定义：

struct RBnode{        //红黑树的结点定义
    int key;          //关键字的值
    RBnode*parent;    //父节点指针
    RBnode*lChild;    //左孩子指针
    RBnode*rchild;    //右孩子指针
    int color;        //结点颜色，如：可用0/1表示黑/红，也可使用枚举型enum表示颜色
};

结点的黑高BH：

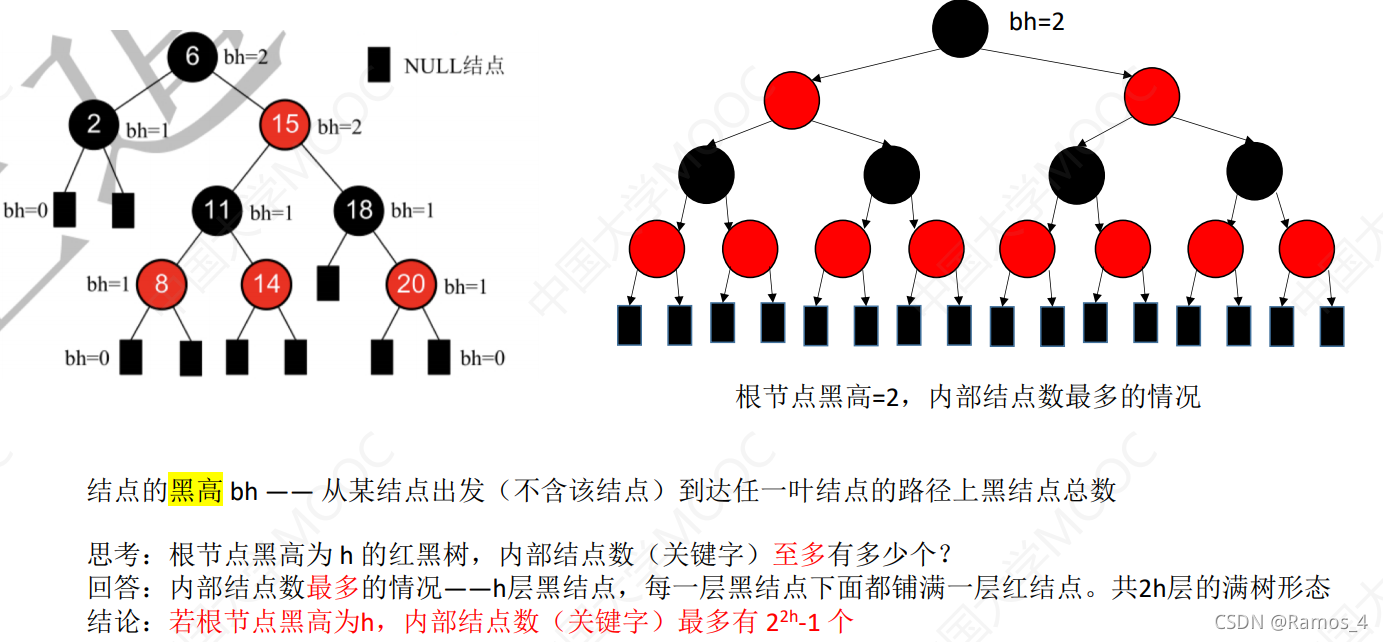
 二、红黑树的查找

与BST、AVL相同，从根出发，左小右大，若查找到一个空叶结点，则查找失败

 三、红黑树的插入规则