数据结构之线性表

线性表，全名为线性存储结构。使用线性表存储数据的方式可以这样理解，即“把所有数据用一根线儿串起来，再存储到物理空间中”。线性表存储数据可细分为顺序存储结构和链式存储结构。对表的操作都可以使用数组来实现。

一、顺序存储结构和链式存储结构：

1. 将数据依次存储在连续的物理空间中，这种存储结构称为顺序存储结构（简称顺序表）；
2. 将数据分散的存储在物理空间中，通过一根线保存着它们之间的逻辑关系，这种存储结构称为链式存储结构（简称链表）。

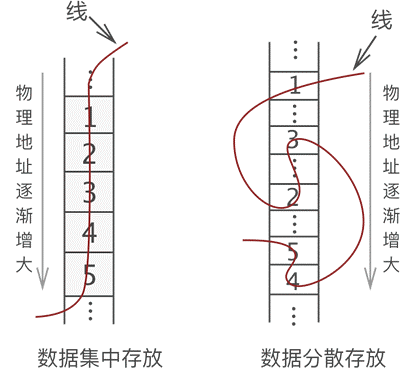
前驱和后继：

数据结构中，一组数据中的每个个体被称为“数据元素”（简称“元素”）。例如，下图 显示的这组数据，其中 1、2、3、4 和 5 都是这组数据中的一个元素。

• 某一元素的左侧相邻元素称为“直接前驱”，位于此元素左侧的所有元素都统称为“前驱元素”；
• 某一元素的右侧相邻元素称为“直接后继”，位于此元素右侧的所有元素都统称为“后继元素”；

二、顺序表的基本操作：

每个数据结构都有集合对数据处理的方法，这能让我们更方便的使用保存在数据结构中的数据。顺序表的基本操作有：增（add)，删(remove)，改(set)，查（find)，插(insert)等。

1.顺序表插入元素：

向已有顺序表中插入数据，根据插入的位置不同，可分为3种情况：

1. 插入顺序表表头；（时间复杂度：O(N)）
2. 在顺序表的表中插入元素；
3. 尾随顺序表已有元素，作为顺序表中最后一个元素。（时间复杂度：O(1)）

虽然数据元素插入顺序表中的位置不同，但都是使用同一方法去解决，即：

1. 通过遍历，找到数据元素要插入的位置；
2. 将要插入位置元素以及后续元素整体向后移动一个位置；
3. 将元素放入腾出来的位置。

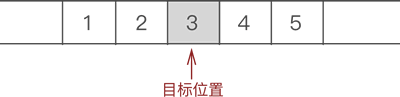
例如，在 {1,2,3,4,5}的第 3 个位置上插入元素 6，实现过程如下：

• 遍历至顺序表存储第 3 个数据元素的位置；

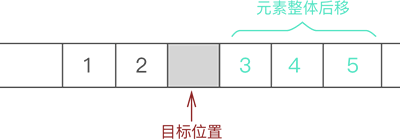
• 将元素 3 以及后续元素 4 和 5 整体向后移动一个位置；

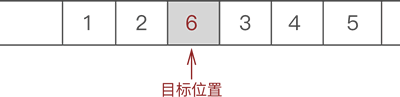
• 将新元素 6 放入腾出的位置。

2.顺序表删除元素

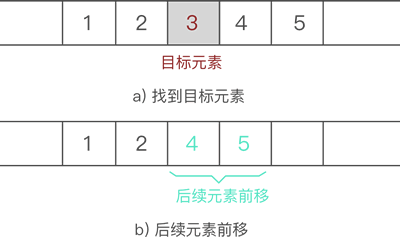
从顺序表中删除指定元素，实现起来非常简单，只需找到目标元素，并将其后续所有元素整体前移 1 个位置即可。通常情况下，后续元素整体前移一个位置，会直接将目标元素删除，从而间接实现删除元素的目的。

例如，从 {1,2,3,4,5} 中删除元素 3 的过程如下图所示：

3.顺序表更改元素

顺序表更改元素的实现过程是：

1. 找到目标元素；
2. 直接修改该元素的值；

4.顺序表查找元素

顺序表中查找目标元素，可以使用多种查找算法实现，比如说二分查找算法、插值查找算法等。

因此，顺序表增（add)，删(remove)，改(set)，查（find)，数据元素的Java语言实现代码如下：

 

三、链表的基本操作：

链表，别名链式存储结构或单链表，用于存储逻辑关系为 "一对一" 的数据。与顺序表不同，链表不限制数据的物理存储状态，换句话说，使用链表存储的数据元素，其物理存储位置是随机的。

例如，使用链表存储 {1,2,3}，数据的物理存储状态如下图所示：

我们看到，上图根本无法体现出各数据之间的逻辑关系。对此，链表的解决方案是，每个数据元素在存储时都配备一个指针，用于指向自己的直接后继元素。如下图所示：

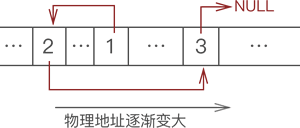
这样，数据元素随机存储，并通过指针表示数据之间逻辑关系的存储结构就是链式存储结构。

链表的节点

从上图可以看到，链表中每个数据的存储都由以下两部分组成：

1. 数据元素本身，其所在的区域称为数据域；
2. 指向直接后继元素的指针，所在的区域称为指针域；

即链表中存储各数据元素的结构如下图所示：

上图所示的结构在链表中称为节点。也就是说，链表实际存储的是一个一个的节点，真正的数据元素包含在这些节点中：

头节点，头指针和首元节点

其实，上图 所示的链表结构并不完整。一个完整的链表需要由以下几部分构成：

1. 头指针：一个普通的指针，它的特点是永远指向链表第一个节点的位置。很明显，头指针用于指明链表的位置，便于后期找到链表并使用表中的数据；
2. 节点：链表中的节点又细分为头节点、首元节点和其他节点：

• 头节点：其实就是一个不存任何数据的空节点，通常作为链表的第一个节点。对于链表来说，头节点不是必须的，它的作用只是为了方便解决某些实际问题；

• 首元节点：由于头节点（也就是空节点）的缘故，链表中称第一个存有数据的节点为首元节点。首元节点只是对链表中第一个存有数据节点的一个称谓，没有实际意义；

• 其他节点：链表中其他的节点；

因此，一个存储 {1,2,3} 的完整链表结构如下图所示：

注意：链表中有头节点时，头指针指向头节点；反之，若链表中没有头节点，则头指针指向首元节点。

1.链表插入元素

同顺序表一样，向链表中增添元素，根据添加位置不同，可分为以下 3 种情况：

• 插入到链表的头部（头节点之后），作为首元节点；
• 插入到链表中间的某个位置；
• 插入到链表的最末端，作为链表中最后一个数据元素；

虽然新元素的插入位置不固定，但是链表插入元素的思想是固定的，只需做以下两步操作，即可将新元素插入到指定的位置：

1. 将新结点的 next 指针指向插入位置后的结点；
2. 将插入位置前结点的 next 指针指向插入结点；

例如，我们在链表 {1,2,3,4} 的基础上分别实现在头部、中间部位、尾部插入新元素 5，其实现过程如下图所示：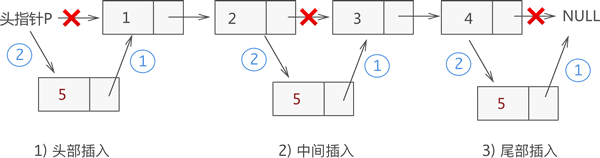

从图中可以看出，虽然新元素的插入位置不同，但实现插入操作的方法是一致的，都是先执行步骤 1 ，再执行步骤 2。

注意：链表插入元素的操作必须是先步骤 1，再步骤 2；反之，若先执行步骤 2，除非再添加一个指针，作为插入位置后续链表的头指针，否则会导致插入位置后的这部分链表丢失，无法再实现步骤 1。

2.链表删除元素

从链表中删除指定数据元素时，实则就是将存有该数据元素的节点从链表中摘除，但作为一名合格的程序员，要对存储空间负责，对不再利用的存储空间要及时释放。因此，从链表中删除数据元素需要进行以下 2 步操作：

1. 将结点从链表中摘下来;
2. 手动释放掉结点，回收被结点占用的存储空间;

例如，从存有 {1,2,3,4} 的链表中删除元素 3，则此代码的执行效果如下图所示：

3.链表更改元素

更新链表中的元素，只需通过遍历找到存储此元素的节点，对节点中的数据域做更改操作即可。

4.链表查找元素

在链表中查找指定数据元素，最常用的方法是：从表头依次遍历表中节点，用被查找元素与各节点数据域中存储的数据元素进行比对，直至比对成功或遍历至链表最末端的 NULL（比对失败的标志）。

注意：遍历有头节点的链表时，需避免头节点对测试数据的影响。

四、顺序表与链表的优缺点比较：

1.顺序表存储（典型的数组）

原理：顺序表存储是将数据元素放到一块连续的内存存储空间，相邻数据元素的存放地址也相邻（逻辑与物理统一）。
优点：

（1）空间利用率高。（局部性原理，连续存放，命中率高） 
（2）存取速度高效，通过下标来直接存储。
缺点：

（1）插入和删除比较慢，比如：插入或者删除一个元素时，整个表需要遍历移动元素来重新排一次顺序。
（2）不可以增长长度，有空间限制,当需要存取的元素个数可能多于顺序表的元素个数时,会出现"溢出"问题.当元素个数远少于预先分配的空间时,空间浪费巨大。  

时间性能：查找 O(1) ,插入和删除O（n）。

2.链表存储

原理：链表存储是在程序运行过程中动态的分配空间，只要存储器还有空间，就不会发生存储溢出问题，相邻数据元素可随意存放，但所占存储空间分两部分，一部分存放结点值，另一部分存放表示结点关系间的指针。
优点：

（1）存取某个元素速度慢。 
（2）插入和删除速度快，保留原有的物理顺序，比如：插入或者删除一个元素时，只需要改变指针指向即可。
（3）没有空间限制,存储元素的个数无上限,基本只与内存空间大小有关. 
缺点：

（1）占用额外的空间以存储指针(浪费空间，不连续存放，malloc开辟，空间碎片多) 
（2）查找速度慢，因为查找时，需要循环链表访问，需要从开始节点一个一个节点去查找元素访问。

时间性能：查找 O(n) ,插入和删除O（1）。 
*频繁的查找却很少的插入和删除操作可以用顺序表存储，堆排序,二分查找适宜用顺序表.
*如果频繁的插入和删除操作很少的查询就可以使用链表存储
*顺序表适宜于做查找这样的静态操作；链表适宜于做插入、删除这样的动态操作。
*若线性表长度变化不大，如果事先知道线性表的大致长度，比如一年12月，一周就是星期一至星期日共七天，且其主要操作是查找，则采用顺序表；若线性表长度变化较大或根本不知道多大时，且其主要操作是插入、删除，则采用链表，这样可以不需要考虑存储空间的大小问题。