11.2 树的应用：前缀码

前缀码

这玩意很有意思啊，假设我们用固定长度的5个byte位来表示26个英文字母，比如：

• 00000：a
• 00001：t

这样当我们想传递单词at的时候，就可以传输01的电信号00000001。但是接下来，试想有没有可能采用下面的形式来表示数据呢？

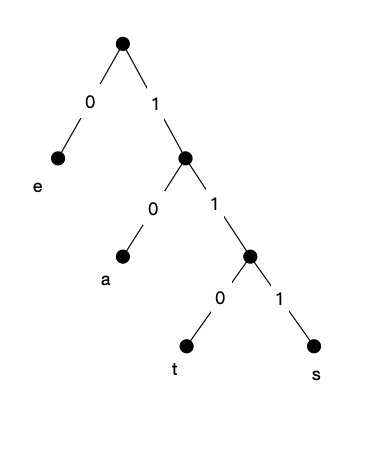
即：

• e的编码为：0
• a的编码为：10
• t的编码为：110
• s的编码为：111

这样当我们想传输teas的时候，就可以传输

t	e	a	s
110	0	10	111

即传输110010111。

这样带来的挑战是什么？就是我们没有办法按照固定长度来分割接收到的二进制数据，但是我们可以比照上面的那个二叉树，直到到达某一个树叶为止。

比如将上面的过程逆着来：

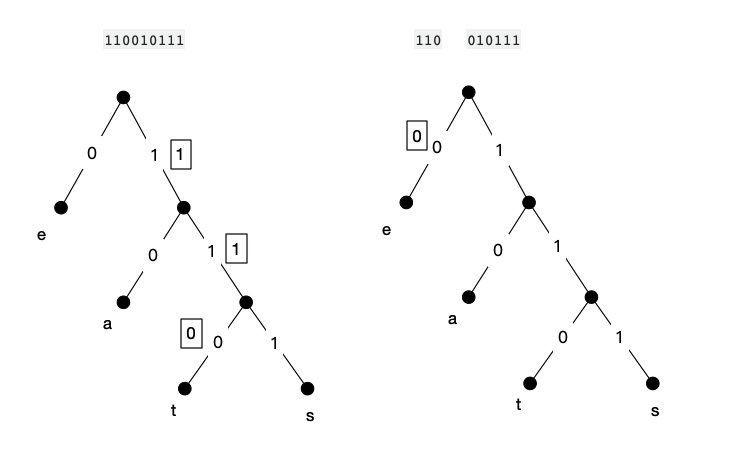
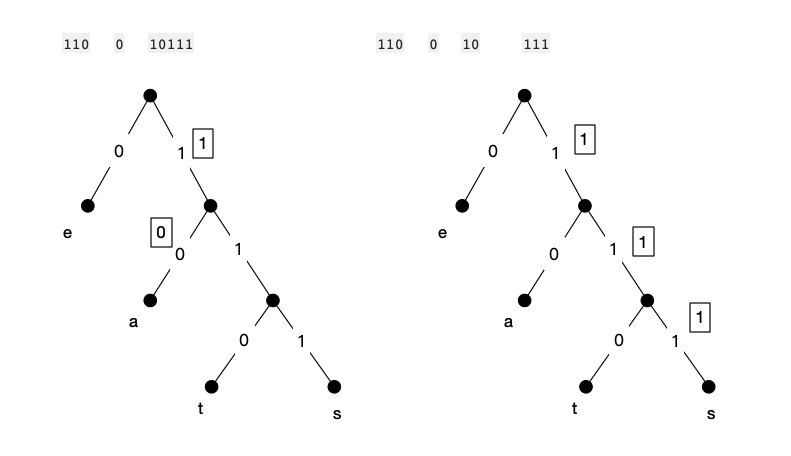
然后像上面这种非固定长度的编码就是前缀码。

哈夫曼编码

参考B站视频

上面是我们随意指定了编码的方式，现在我们需要先构建一颗树，然后再套用到上面的方式中。比如下面这句话：

To be,or not to be:that is the question

然后我们统计各个字符号出现的频率：

• T : 0.03
• o : 0.13
• 空格: 0.18
• b : 0.05
• e : 0.1
• , : 0.03
• r : 0.03
• n : 0.05
• t : 0.15
• : : 0.03
• h : 0.05
• a : 0.03
• i : 0.05
• s : 0.05
• q : 0.03
• u : 0.03

然后我们从中挑选最小的两个值，如果有很多最小的值也没关系，随便挑两个：

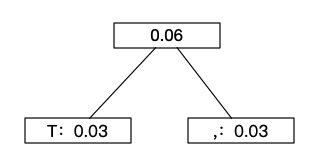
然后这里我们就可以把上面的T和,(逗号)去除掉了，加上一个新的频率值：0.06，然后再来挑2个最小值：

然后继续上面的步骤，直到完成下面这幅图：

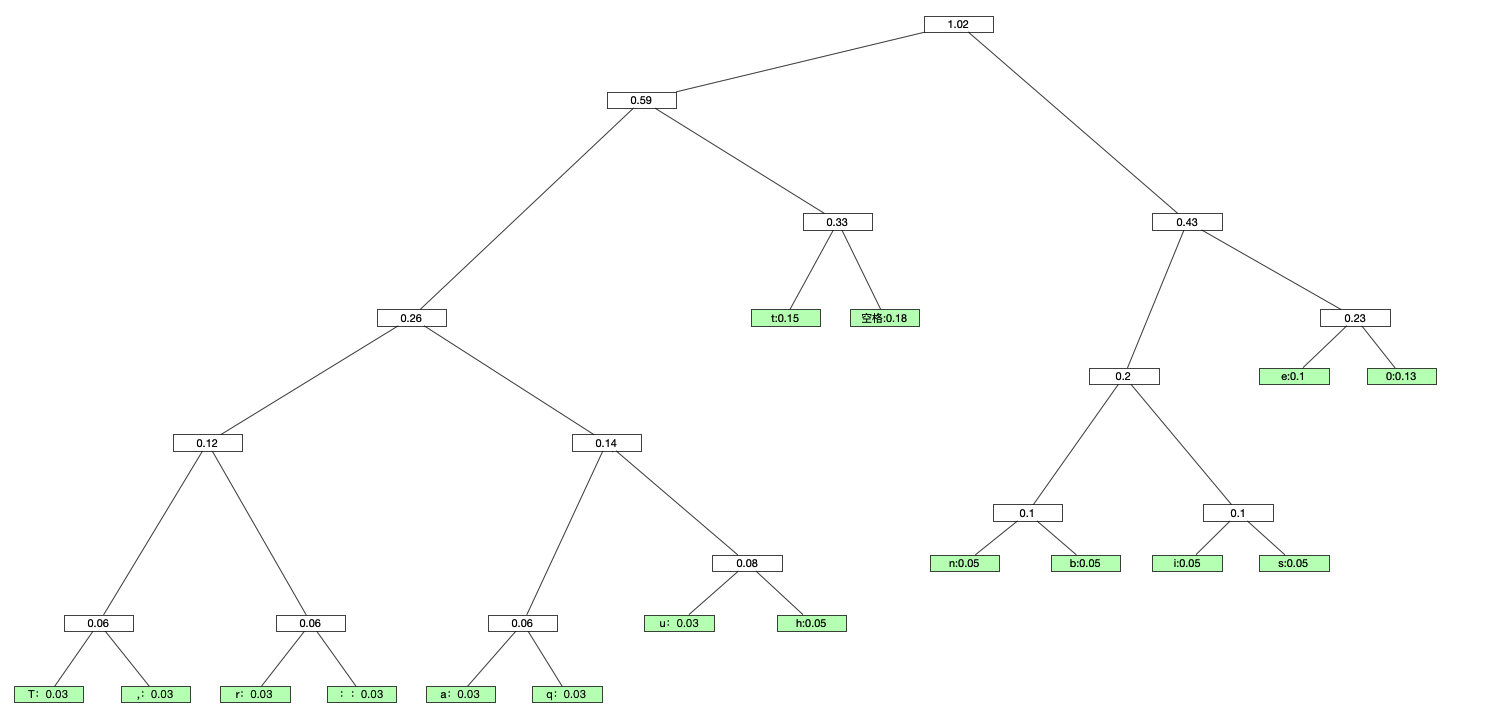
因为图片太大了，我估计缩小会糊，所以放一下原图的地址

这里说一下构建的方法，依次选择上面列表中最小的点，然后组建成新的顶点，就这样。构建好哈夫曼树之后，就可以套用到上面的二叉树编码中去了。

同样放一下原图地址

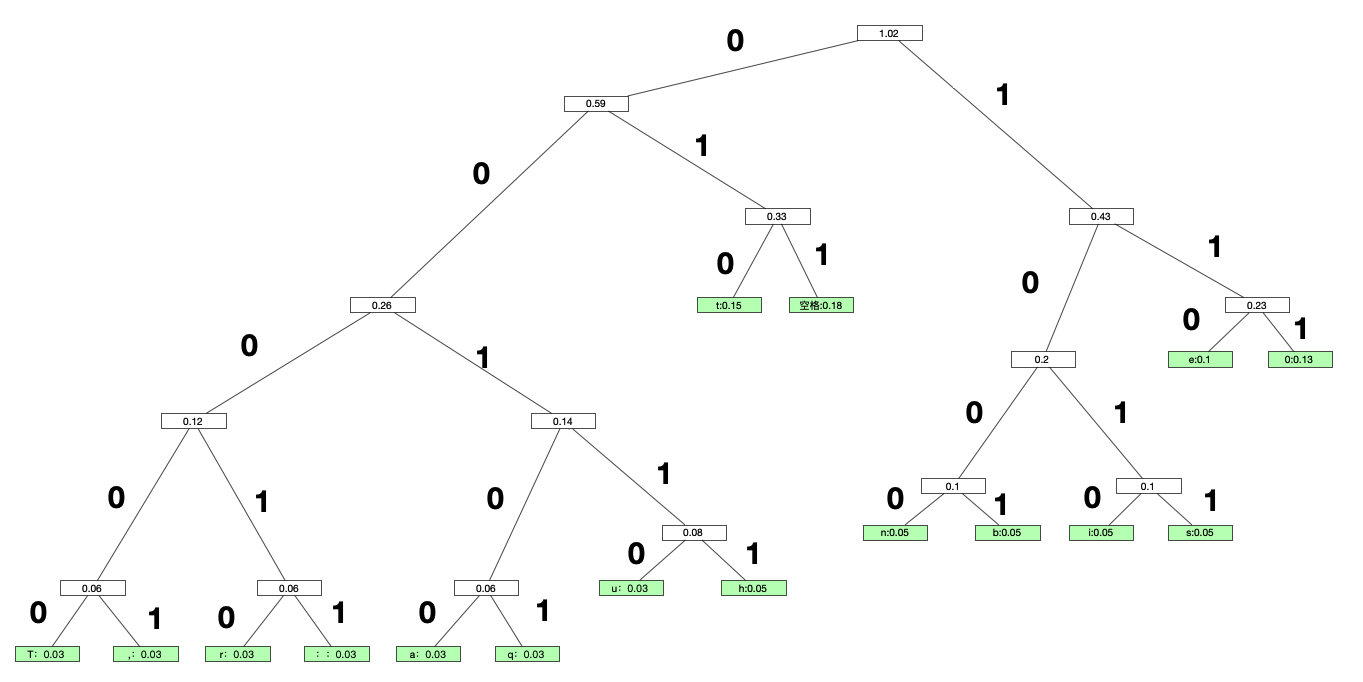
这样就可以得到例如T的编码就是：00000，,的编码就是00001。

这样的好处就是频率比较高的字符，比如t，它的编码就比较短010。

另外这里总数是1.02，而不是1是因为上面的数据是我用代码算出来的，精度上有点偏差。

哈夫曼树具体代码

这段代码真的是写死我了：

<?php

/**
 * Class Leaf
 * 记录下各种数据结构的类
 */
class Leaf{
    public $value;
    public $label;
    // 用来构建哈夫曼树
    public $leftLeaf;
    public $rightLeaf;
    // 用来保存最终的编码值
    public $code;
    /**
     * 模拟链表操作，跟树操作无关
     * @var $nextLeaf Leaf
     */
    public $nextLeaf;
    public function __construct($value='',$label='')
    {
        $this->value=$value;
        $this->label=$label;
    }
}

/**
 * 将字符串转化成上面的类
 * @param $string
 * @return Leaf
 */
function prepareLeaves($string){
    $length=strlen($string);
    $result=[];
    for ($i=0;$i<$length;$i++){
        $data=$string[$i];
        !isset($result[$data]) && $result[$data]=0;
        $result[$data]++;
    }
    $prepare=false;
    $leaf=new Leaf();
    foreach ($result as $word=>$count){
        $value=round($count/$length,2);
        if (!$prepare){
            $prepare=true;
            $leaf->value=$value;
            $leaf->label=$word;
            continue;
        }
        $newLeaf=new Leaf($value,$word);
        $leaf=sortLeaf($leaf,$newLeaf);
    }
    return $leaf;
}

/**
 * 构建哈夫曼树
 * @param $leaf Leaf
 */
function createHuffmanTree($leaf){
    if (!$leaf->nextLeaf->nextLeaf){
        $indexLeaf=new Leaf($leaf->value+$leaf->nextLeaf->value);
        $indexLeaf->leftLeaf=$leaf;
        $indexLeaf->rightLeaf=$leaf->nextLeaf;
        return $indexLeaf;
    }
    $newLeaf=new Leaf($leaf->value+$leaf->nextLeaf->value);
    $newLeaf->leftLeaf=$leaf;
    $newLeaf->rightLeaf=$leaf->nextLeaf;
    // 插入新的顶点并排序，保证最前面的2个一定是值最小的2个顶点
    $leaf=sortLeaf($leaf->nextLeaf->nextLeaf,$newLeaf);
    // 递归，并且之前用过的2个顶点不再继续使用
    return createHuffmanTree($leaf);
}

/**
 * 根据哈夫曼树在其中加上编码值
 * @param $leaf Leaf
 * @param string $preCode
 * @return bool
 */
function getWordCode($leaf,$preCode=''){
    if (!$leaf){
        return false;
    }
    if ($leaf->leftLeaf){
        $leaf->leftLeaf->code=$preCode."0";
        getWordCode($leaf->leftLeaf,$leaf->leftLeaf->code);
    }
    if ($leaf->rightLeaf){
        $leaf->rightLeaf->code=$preCode."1";
        getWordCode($leaf->rightLeaf,$leaf->rightLeaf->code);
    }
}

/**
 * 读取最终的编码值，保存在 result 数组中
 * @param $leaf Leaf
 * @param $result array
 * @return array
 */
function storeResult($leaf,&$result){
    if (!$leaf){
        return $result;
    }
    if ($leaf->label){
        $result[$leaf->label]=$leaf->code;
    }
    storeResult($leaf->leftLeaf,$result);
    storeResult($leaf->rightLeaf,$result);
}

/**
 * 按照从小到大排序叶子节点
 * @param $leaf Leaf
 * @param $newLeaf Leaf
 * @return Leaf
 */
function sortLeaf($leaf,$newLeaf):Leaf{
    if ($leaf->value>$newLeaf->value){
        $newLeaf->nextLeaf=$leaf;
        return $newLeaf;
    }
    $thisLeaf=$leaf->nextLeaf;
    $lastLeaf=$leaf;
    if (!$thisLeaf){
        $leaf->nextLeaf=$newLeaf;
        return $leaf;
    }
    while ($thisLeaf->nextLeaf && $thisLeaf->value<$newLeaf->value){
        $lastLeaf=$thisLeaf;
        $thisLeaf=$thisLeaf->nextLeaf;
    }
    $lastLeaf->nextLeaf=$newLeaf;
    $newLeaf->nextLeaf=$thisLeaf;
    return $leaf;
}

上面是具体的操作代码，下面是调用：

<?php
$string='To be,or not to be:that is the question';
$indexLeaf=prepareLeaves($string);
$indexLeaf=createHuffmanTree($indexLeaf);
getWordCode($indexLeaf);
$storeResult=[];
storeResult($indexLeaf,$storeResult);
print_r($storeResult);

最终输出的结果：

Array
(
    [o] => 0
    [ ] => 100
    [n] => 10100
    [b] => 10101
    [i] => 10110
    [h] => 10111
    [e] => 1100
    [:] => 110100
    [r] => 110101
    [q] => 110110
    [a] => 110111
    [T] => 111000
    [u] => 111001
    [,] => 111010
    [s] => 111011
    [t] => 1111
)

这里有个很有意思的地方，那就是o的编码是最短的，这个问题的答案我在代码中暂时没有找到原因，所以先搁置吧。