首先通过一个例子说一下语言模型:
RNN优点:
- 可以处理任意长度的输入
- weights在所有时刻都是共享的
- 可以利用前面时刻的信息
RNN缺点:
- 耗时,无法并行
- 实际中,很难利用前面很远时刻的信息
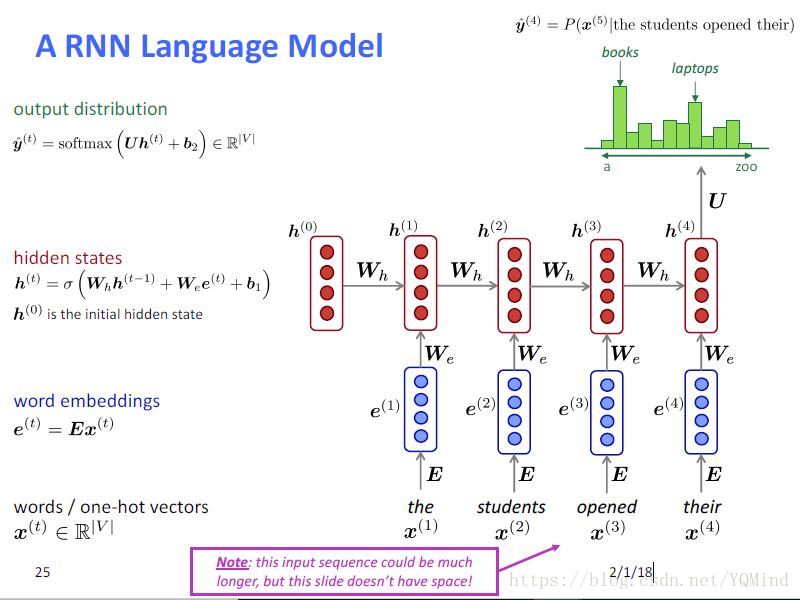
RNN公式:
h
t
=
t
a
n
h
(
W
h
h
t
−
1
+
W
e
e
t
+
b
1
)
h_t = tanh (W_hh_{t-1} + W_ee_t + b_1)
ht=tanh(Whht−1+Weet+b1)
o
t
=
s
o
f
t
m
a
x
(
U
h
t
+
b
2
)
o_t = softmax(Uh_t+b_2)
ot=softmax(Uht+b2)
其中,
W
h
,
W
e
,
b
1
,
U
,
b
2
W_h, W_e, b_1, U, b_2
Wh,We,b1,U,b2只有一套。
RNN可能会遭遇梯度消失或梯度爆炸问题:
∂
E
∂
W
=
∑
1...
T
∂
E
t
∂
W
\frac{\partial E}{\partial W} = \sum_{1 ... T} \frac {\partial E_t}{\partial W}
∂W∂E=∑1...T∂W∂Et
其中
∂
E
t
∂
W
=
∑
1...
t
∂
E
t
∂
o
t
∂
o
t
∂
h
t
∂
h
t
∂
h
k
∂
h
k
∂
W
\frac {\partial E_t}{\partial W} = \sum_{1 ... t } \frac {\partial E_t}{\partial o_t} \frac {\partial o_t}{\partial h_t}\frac {\partial h_t}{\partial h_k} \frac {\partial h_k}{\partial W}
∂W∂Et=∑1...t∂ot∂Et∂ht∂ot∂hk∂ht∂W∂hk
其中
∂
h
t
∂
h
k
\frac {\partial h_t}{\partial h_k}
∂hk∂ht 可以很大或很小。注意到
∂
h
j
∂
h
j
−
1
\frac {\partial h_j}{\partial h_{j-1}}
∂hj−1∂hj是向量对向量求导,结果是一个Jacobian矩阵,矩阵元素是每个点的导数。
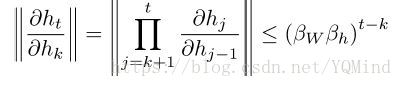
RNN很难训练,主要是因为存在梯度消失和梯度爆炸的问题。
对于梯度爆炸,使用Gradient clipping(梯度截断)。

对于梯度消失,可以选择好的初始化,使用Relu激活函数。但是主要的方法还是使用GRU和LSTM。
[1] https://blog.youkuaiyun.com/apsvvfb/article/details/52848554
[2] https://www.toutiao.com/i6491156699737489933/?group_id=6491156699737489933&group_flags=0
[3] https://blog.youkuaiyun.com/zhangxb35/article/details/70060295
























 2721
2721

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








