【剑指offer】【C++】68 - II. 二叉树的最近公共祖先

1 题目

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

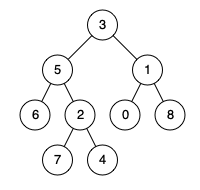
例如，给定如下二叉树:  root = [3,5,1,6,2,0,8,null,null,7,4]


示例 1:

输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出: 3
解释: 节点 5 和节点 1 的最近公共祖先是节点 3。
示例 2:

输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出: 5
解释: 节点 5 和节点 4 的最近公共祖先是节点 5。因为根据定义最近公共祖先节点可以为节点本身。
 

说明:

所有节点的值都是唯一的。
p、q 为不同节点且均存在于给定的二叉树中。
注意：本题与主站 236 题相同：https://leetcode-cn.com/problems/lowest-common-ancestor-of-a-binary-tree/

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/er-cha-shu-de-zui-jin-gong-gong-zu-xian-lcof
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

2 主要思路：

考点：后序遍历

• 后序遍历可以自底向上的遍历判断。
• 在递归函数体内部，其中的root并不仅仅指代整棵树的根节点，而是指后序遍历过程中的每棵子树的根节点。因此在考虑判别条件的时候，不仅考虑叶子节点处的情况，还要考虑内部子树的情况。因此在越过叶子节点的节点处为空，则返回空，如果内部子树中节点等于已有点p、q的值，那么就返回这个节点。
• 在返回信息时，有信息传递。在左右递归函数后，是站在左右孩子的双亲角度考虑，而此双亲作为孩子时，可能为左节点或者右节点。因此站在此双亲的角度考虑，如果两个孩子返回为空，说明没有一个结点与p、q相等，此双亲也返回空；如果均不为空，说明有一或二个节点等于p或者q，如果是左节点为空，那么就返回右节点，如果右节点为空，那么返回左节点，否则左右节点均不为空，说明此双亲就是最近的祖先节点。

下图是剑指offer的题解：

3 代码：

class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if(!root||root->val==p->val||root->val==q->val) return root;
        TreeNode* left = lowestCommonAncestor(root->left, p, q);
        TreeNode* right = lowestCommonAncestor(root->right, p, q);
        if(!left&&!right) return nullptr;
        else if(!left) return right;
        else if(!right) return left;
        else return root;
    }
};