【剑指offer】【C++】54. 二叉搜索树的第k大节点

最新推荐文章于 2025-03-04 21:24:50 发布

「已注销」

最新推荐文章于 2025-03-04 21:24:50 发布

阅读量394

点赞数 1

CC 4.0 BY-SA版权

分类专栏： C++ 剑指offer

本文链接：https://blog.youkuaiyun.com/YJYS_ZHX/article/details/117339510

C++ 同时被 2 个专栏收录

39 篇文章

订阅专栏

剑指offer

19 篇文章

订阅专栏

本文介绍了如何利用中序遍历解决二叉搜索树的第k大节点问题。通过倒序中序遍历，每次递减k值，当k等于0时保存节点值。在遍历过程中，利用类的成员变量保存结果，避免使用局部变量。当k减到0时，立即返回，防止不必要的递归调用。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

给定一棵二叉搜索树，请找出其中第k大的节点。

 

示例 1:

输入: root = [3,1,4,null,2], k = 1
   3
  / \
 1   4
  \
   2
输出: 4
示例 2:

输入: root = [5,3,6,2,4,null,null,1], k = 3
       5
      / \
     3   6
    / \
   2   4
  /
 1
输出: 4
 

限制：

1 ≤ k ≤ 二叉搜索树元素个数

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/er-cha-sou-suo-shu-de-di-kda-jie-dian-lcof
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

1 主要思想：

考点：二叉搜索树的中序遍历。

1）什么是二叉搜索树？

由题目中的二叉树可知，这是二叉搜索树或者二叉排序树、二叉查找树。其主要特征是：

如果左孩子不为空，那么其值小于根节点；
如果右孩子不为空，那么其值大于根节点；
以左孩子为根的子树以及以右孩子为根的子树同样满足上述要求。

通俗说就是，左孩子的值 < 根节点的值 < 右孩子的值
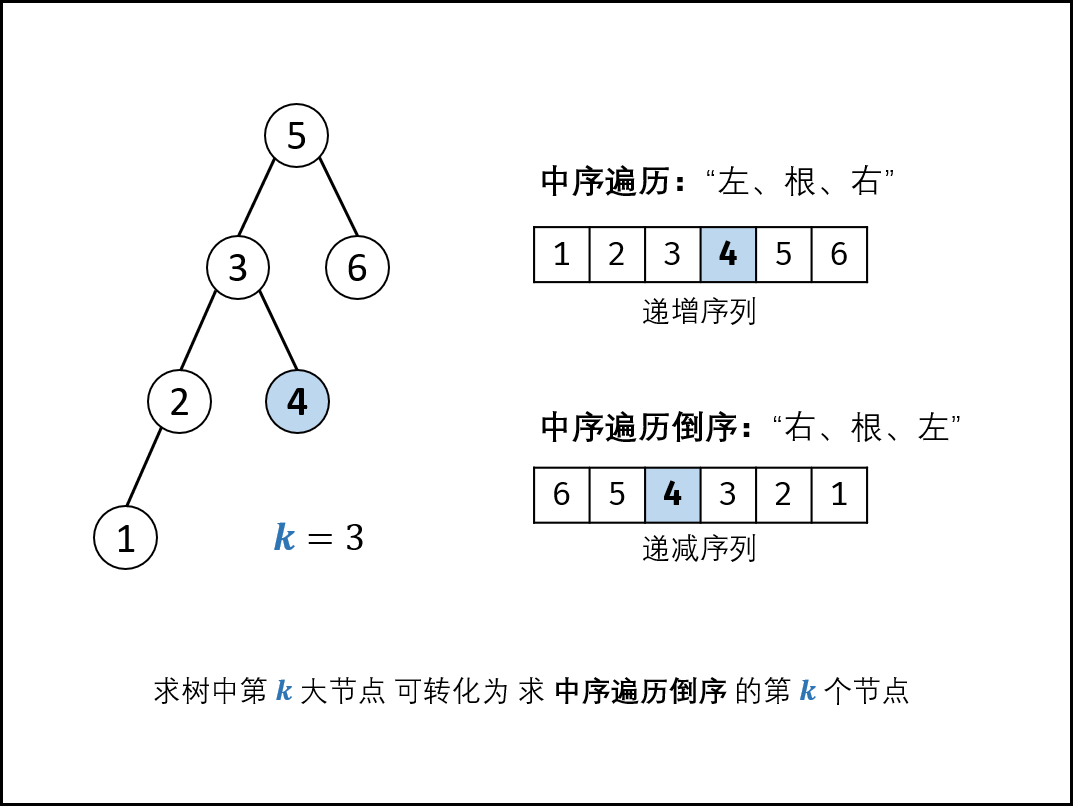
在这里插入图片描述

2）为什么提到中序遍历？

由于树的特殊性，我们可以看到，左孩子的值 < 根节点的值 < 右孩子的值，那么我们通过中序遍历就可以得到一个有序的序列，并且这个序列的数值从小到大排列，也就是递增的序列。看代码块：

void df(TreeNode* root)
{
	if(!root) return;
	
	df(root->left);
	//访问完左边后，函数返回到了小树的根节点处
	df(root->right);
}

3）主要的问题是什么？

如何获得第K大的数？

对于二叉搜索树来说，正常的中序遍历先访问左孩子，而后右孩子，得到的序列是从小到大排列。可以先访问右孩子（大）后访问左孩子，得到的序列是从大到小排列，容易求得第k大的数。
可以通过递归来实现二叉树的中序遍历，使用k作为计数值，每访问一个就 - -k；直到k==0为止，此时将数值保存下来即可。
得到了第k大的数，后续的递归操作其是不需要在进行的，但是前面的函数已经压入栈中了，应该如何操作？也就是如何让递归停止呢？

计数的数值递减操作应该放在哪里？

当访问到叶子节点时，由于其左孩子为空，因此将左孩子传入函数直接就返回，此时落在了此叶子节点上，而后再将右孩子传入函数，右孩子也为空，也直接返回。因此可以操作的地方就是两个函数中间的地方，也就是程序正好落在当前的节点上时，可以对k进行操作，以及判断是否为零。

如何保存第k大的数？

保存第k大的数，同时还不想再继续递归下去，也就是找到第k大数后，要快速的返回，不能再递归下去了。如果使用递归函数来返回这样的值，那么层层递归最终回到树的根节点而后进入左子树，数值保存不下来，因为递归中的变量是局部变量，除非是传入的引用或者指针。因此将使用类的成员变量来保存数据。而返回值采void。

如何让递归停止呢？
假如k=5,5-0=5；因此当k递减到0时，保存节点数值到成员变量中，而在k为其他数值时并不保存。另外，我们并不想执行未压入栈中的函数内的递归调用，但是栈中的函数是必须要继续执行完毕的。因此k的值还是会继续减小的，判断k<=0时，就直接return即可，而不是去调用当前节点的左孩子节点的函数（这样的操作会导致继续递归调用）。

4）总结：

通过设置成员变量res（保存第k大的数值）以及k（放置k值），而不是使用递归内的局部变量（因为使用局部变量最后必须要return，而后就被销毁了）。使用倒的中序遍历来从大到小来访问节点数值，由于进行过右孩子的函数调用后，会落脚到当前的节点处，因此在两个函数中间进行相关操作。通过逐渐减小k值直到为0时才保存数值到res中，而为了提高效率，不再访问栈中函数可能带来的递归调用，我们通过判断k<=0是否满足，满足的话就直接return即可。

2 代码：

class Solution {
public:
    int kthLargest(TreeNode* root, int k) {
        if(!root||!k) return -1;//判断给定的初始数值是否满足条件很重要
        this->k = k;

        df(root); 
        return this->res;       
    }
    void df(TreeNode* root){
        if(!root) return;//其实有这句话后，就不需要再判断左右孩子节点是否为空，因为当前节点为叶子节点时，左右孩子均为空，调用此函数就会直接返回啦
        df(root->right);
        if(--k==0) this->res = root->val;
        if(k<=0) return;//此处防止栈中的函数内可能存在的递归调用
        df(root->left); 
    }
private:
    int res, k;
};

3 其他优秀代码：

class Solution {
public:
//二叉树的中序遍历
    int cnt=0,res=0;
    int kthLargest(TreeNode* root, int k) {
        dfs(root,k);
        return res;
    }
    void dfs(TreeNode* root,int k){//因为是第k大，所以先遍历右子树再遍历左子树
        if(!root)return;
        dfs(root->right,k);
        cnt++;
        if(cnt==k){
            res=root->val;
            return;
        }
        dfs(root->left,k);
    }
};