支持向量机算法由Vladimir Vapnik提出,用于解决线性可分问题,再将线性可分问题中获得的结论推广到线性不可分情况。
1.线性可分和非线性可分(二分类情况下)
如果特征空间是二维的,如果存在一条直线能将训练样本分开,就是线性可分,否则为线性不可分
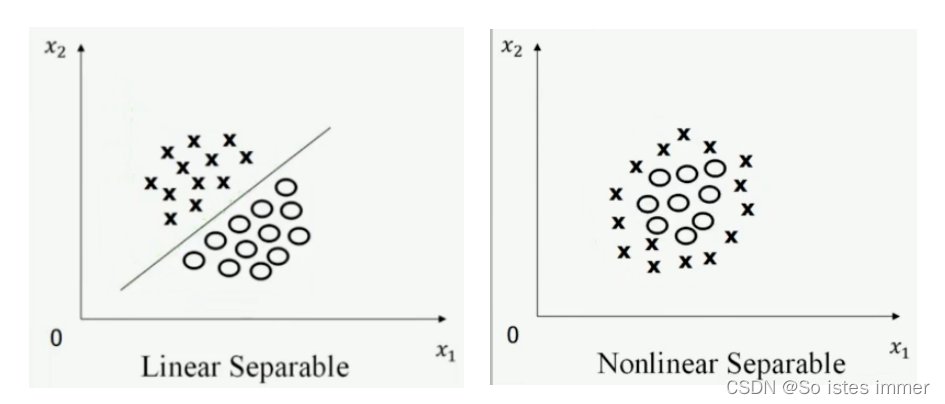
在三维特征空间中的线性可分,是用一个平面去分隔训练样本。
特征空间维度>=4时,用超平面(Hyperplane)去分隔。
下面用数学严格定义线性可分
假设我们有N个训练样本和他们的标签,{(X1,y1),(X2,y2),...,(XN,yN)} ,Xi=,yi={+1,-1}
如果yi=+1,Xi属于c1,如果yi=-1,Xi属于c2
在i=1~N线性可分,是指存在(w1,w2,b),使得对i=1~N,有


2.二维特征空间中寻找最优分类直线
要满足的条件
①该直线分开了两类
②该直线最大化间隔margin
③该直线处于间隔的中间,到所有支持向量的距离相等



























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










