homework_2---用python实现代码蒙特卡罗方法手搓图形（以圆为例）

蒙特卡罗方法是一种通过随机采样来解决问题的统计方法。我们可以用它来估算圆周率，或者生成一些有趣的图形。下面是一个用蒙特卡罗方法生成图形的简单示例：通过随机点来绘制一个圆。

代码解释：

1. ​​随机点生成​​：生成 num_points 个随机点，每个点的 x 和 y 坐标都在 [-1, 1] 范围内。
2. ​​判断点是否在圆内​​：通过计算 x^2 + y^2 是否小于等于 1 来判断点是否在单位圆内。
3. ​​估算圆周率​​：根据蒙特卡罗方法，圆的面积与正方形面积的比值可以用来估算圆周率。公式为：π ≈ 4 * (points_inside / total_points)。
4. ​​绘制图形​​：使用 matplotlib 绘制所有点，蓝色点表示在圆内，红色点表示在圆外。

运行结果：

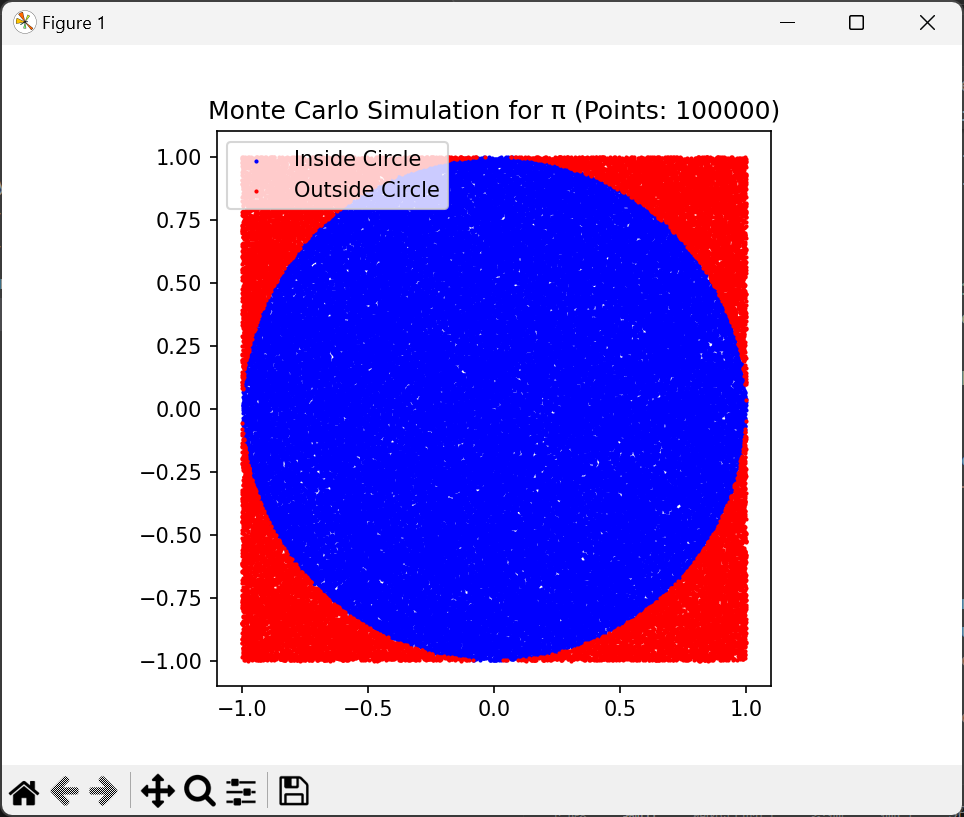
运行代码后，你会看到一个散点图，蓝色点集中在单位圆内，红色点分布在圆外。同时，控制台会输出估算的圆周率值。

完整代码

import random
import matplotlib.pyplot as plt

def monte_carlo_circle(num_points):
    inside_circle = 0
    points_inside = []
    points_outside = []

    for _ in range(num_points):
        x = random.uniform(-1, 1)
        y = random.uniform(-1, 1)
        
        # 判断点是否在圆内
        if x**2 + y**2 <= 1:
            inside_circle += 1
            points_inside.append((x, y))
        else:
            points_outside.append((x, y))

    # 估算圆周率
    pi_estimate = 4 * inside_circle / num_points
    print(f"Estimated value of π: {pi_estimate}")

    # 绘制图形
    fig, ax = plt.subplots()
    ax.scatter(*zip(*points_inside), color='blue', s=1, label='Inside Circle')
    ax.scatter(*zip(*points_outside), color='red', s=1, label='Outside Circle')
    ax.set_aspect('equal', 'box')
    ax.legend()
    ax.set_title(f"Monte Carlo Simulation for π (Points: {num_points})")
    plt.show()

# 设置随机点的数量
num_points = 100000
monte_carlo_circle(num_points)